MACIERZE I WYZNACZNIKI
MACIERZE
Definicja macierzy:
Niech dane będą dwa zbiory skończone M={1,2,...,m} i N={1,2,...,n}. Macierzą prostokątną wymiaru mxn o wyrazach rzeczywistych nazywamy funkcję przyporządkowującą uporządkowanej parze liczb naturalnych (i, j), gdzie i![]()
M, j![]()
N, dokładnie jedną liczbę rzeczywistą aij.
Macierz zapisujemy w postaci tablicy:

gdzie:
poziome rzędy tablicy nazywamy wierszami
pionowe rzędy tablicy nazywamy kolumnami
aij oznacza element macierzy stojący w i-tym wierszu i j-tej kolumnie.
Macierz o wymiarze mxn oznaczamy symbolem:
![]()
lub [aij]mxn
W przypadku, kiedy można pominąć wymiar macierzy, i nie prowadzi to do nieporozumień, macierze oznaczamy stosując tylko wielkie litery alfabetu, np. A, B, X itp.
Definicja wymiaru macierzy:
Wymiarem macierzy nazywamy uporządkowaną parę liczb naturalnych mxn, której pierwszy wyraz oznacza liczbę wierszy macierzy, a drugi liczbę kolumn.
Definicja macierzy zerowej:
Macierz wymiaru mxn, w której wszystkie elementy są równe 0 nazywamy macierzą zerową wymiaru mxn i oznaczamy przez 0mxn lub przez 0, gdy znany jest jej wymiar.
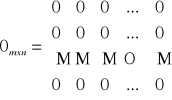
Definicja macierzy kwadratowej:
Macierz, w której liczba wierszy jest równa liczbie kolumn, tj. m=n, nazywamy macierzą kwadratową. Liczbę wierszy (kolumn) nazywamy wtedy stopniem macierzy kwadratowej. Elementy macierzy, które mają ten sam numer wiersza co kolumny tworzą główną przekątną macierzy.
Przykład macierzy kwadratowej

stopnia 4
Definicja macierzy kolumnowej:
Macierzą kolumnową (nazywaną również macierzą jednokolumnową lub wektorem kolumnowym) nazywamy macierz o wymiarze mx1.
![]()
Przykład macierzy kolumnowej:
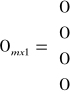
Definicja macierzy wierszowej:
Macierzą wierszową (nazywaną również macierzą jednowierszową lub wektorem wierszowym) nazywamy macierz o wymiarze 1xn.
![]()
Definicja macierzy trójkątnej dolnej:
Macierz kwadratową stopnia n>2, w której wszystkie elementy stojące nad główną przekątną są równe 0, nazywamy macierzą trójkątną dolną.
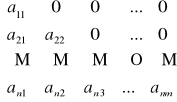
Definicja macierzy trójkątnej górnej:
Macierz kwadratową stopnia n>2, w której wszystkie elementy stojące pod główną przekątną są równe 0, nazywamy macierzą trójkątną górną.
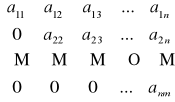
Definicja macierzy diagonalnej:
Macierz kwadratową stopnia n, w której wszystkie elementy nie stojące na głównej przekątnej są równe 0, nazywamy macierzą diagonalną (lub macierzą przekątną), ozn. diag (a11, a22, ..., amn).
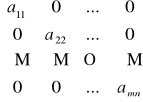
Przykład macierzy diagonalnej:
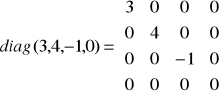
Definicja macierzy skalarnej:
Macierz diagonalną stopnia n, w której wszystkie elementy stojące na głównej przekątnej są sobie równe, nazywamy macierzą skalarną.
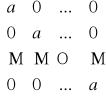
Definicja macierzy jednostkowej:
Macierz skalarną stopnia n, w której wszystkie elementy stojące na głównej przekątnej są równe 1, nazywamy macierzą jednostkową. Macierz jednostkową stopnia n oznaczamy przez In lub En, albo - gdy znany jest stopień - przez I lub E.
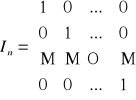
DZIAŁANIA NA MACIERZACH:
Definicja równości macierzy:
Macierze A i B są równe, co zapisujemy A=B, wtedy i tylko wtedy, gdy są tego samego wymiaru, tj. A=[aij]mxn i B=[bij]mxn, oraz odpowiednie elementy macierzy są równe, tzn. aij=bij, dla i=1,2,...,m; j=1,2,...,n.
Definicja sumy macierzy:
Sumą macierzy A=[aij]mxn i B=[bij]mxn nazywamy macierz C=[cij]mxn, której elementy są określone wzorem:
cij=aij+bij
dla i=1,2,...,m ; j=1,2,...,n. Piszemy wtedy C=A+B.
UWAGA: Dodajemy tylko macierze o tych samych wymiarach!!!
Przykład: Obliczyć sumę macierzy A i B, gdzie:
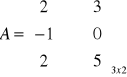
i 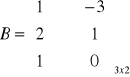
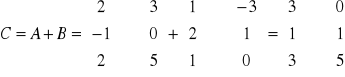
Definicja iloczynu macierzy przez liczbę:
Iloczynem macierzy A=[aij]mxn przez liczbę λ, λ![]()
R, nazywamy macierz B=[bij]mxn, której elementy określone są wzorem:
bij= λaij
dla i=1,2,...,m ; j=1,2,...,n. Piszemy wtedy B= λA.
Przykład: Obliczyć D=2A, dla λ=-2
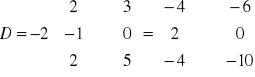
UWAGA: Macierz -A, rozumianą jako macierz (-1)∙A, nazywamy macierzą przeciwną do A. Wówczas różnicą macierzy A i B rozumiemy jako sum macierzy A i macierzy przeciwnej do B, tj. A-B=A+(-B).
FAKT: Własności działań na macierzach:
Niech A, B i C będą dowolnymi macierzami tego samego wymiaru oraz niech α i β będą liczbami rzeczywistymi. Wówczas:
A+B=B+A
A+(B+C)=(A+B)+C
A+0=0+A=A
A+(-A)=0
α(A+B)= αA+αB
(α+ β)A= αA+βA
(αβ)A= α(βA)
1∙A=A
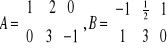
Przykład: Rozwiązać równanie macierzowe 3(A+X)+5(3X+B)=A-B, gdzie
3A+3X+5(3X)+5B=A-B
3A+3X+15X+5B=A-B
3A+18X+5B=A-B/![]()
18X=-2A-6B/![]()
X=![]()
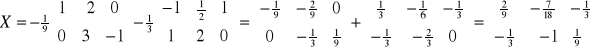
Definicja iloczynu macierzy:
Niech macierz A=[aij] ma wymiar mxn, a macierz B=[bij] wymiar nxp. Iloczynem macierzy A i B nazywamy macierz C=[cij] wymiaru mxp, której elementy określone są wzorem:
![]()
dla i=1,2,...,m ; j=1,2,...,p. Piszemy wtedy C=AB.
AmxnBnxp=Cmxp
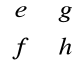
SCHEMAT:
a11 a12
a21 a22
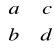
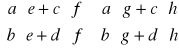
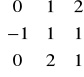
Przykład: Obliczyć AB, gdzie 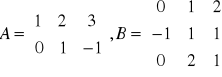
A2x3 B3x3
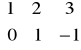
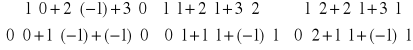
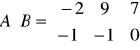
UWAGA: Element cij iloczynu macierzy A i B otrzymujemy sumując iloczyny odpowiadających sobie elementów i-tego wiersza i j-tej kolumny macierz B.
UWAGA: Iloczyn macierzy A i B jest określony tylko wtedy, gdy liczba kolumn macierzy A jest równa liczbie wierszy macierzy B.
FAKT: Własności iloczynu macierzy:
Niech macierz A ma wymiar mxn, a macierze B i C wymiar nxk. Wówczas:
A(B+C)=AB+AC
Niech macierze A i B mają wymiar mxn a macierz C wymiar nxk. Wówczas:
(A+B)=AC+BC
Niech macierz A ma wymiar mxn, a macierz B wymiar nxk oraz niech α będzie liczbą rzeczywistą. Wówczas:
A(αB)=(αA)B=α(AB)
Niech macierz A ma wymiar mxn, macierz B wymiar nxk, a macierz C wymiar kxl. Wówczas:
(AB)C=A(BC)
Niech macierz A ma wymiar mxn. Wówczas:
AIn=ImA=A
UWAGA: Mnożenie macierzy nie jest na ogół przemienne.
Przykład: A2x3 ∙B2x2 - nie jest określone!!!
Przykład: Niech 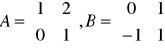
. Obliczyć AB i BA.
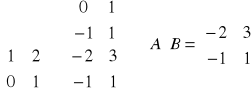
A∙B![]()
B∙A - macierze te są określone ale są różne!!!

UWAGA: Niech macierz A jest macierzą kwadratową. Wówczas zamiast AA...A (n razy) będziemy pisali An.
Definicja macierzy transponowanej:
Niech macierz A=[aij] będzie macierzą transponowaną wymiaru mxn. Macierzą transponowaną do macierzy A nazywamy macierz B=[bij] wymiaru nxm, której elementy są określone wzorem:
bij=aij
dla i=1,2,...,n ; j=1,2,...,m. Macierz transponowaną do A oznaczamy przez AT.
Przykład: Transponowanie macierzy:
Niech 
Wówczas 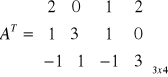
FAKT: Własności transpozycji macierzy:
Niech A i B będą macierzami wymiaru mxn. Wówczas:
(A+B)T=AT+BT
Niech A będzie macierzą wymiaru mxn oraz niech α będzie liczbą rzeczywistą. Wówczas:
(AT)T=A oraz (αA)T=αAT
Niech A będzie macierzą wymiaru mxn, a B macierzą wymiaru nxk. Wówczas:
(AB)T=BTAT
Niech A będzie macierzą kwadratową oraz niech k

N. Wówczas:
(Ak)T=(AT)k
Definicja macierzy symetrycznej:
Macierz kwadratową A stopnia n, dla której zachodzi warunek: AT=A nazywamy macierzą symetryczną.
Przykład: Macierz symetryczna:

- symetria elementów względem głównej przekątnej.
AT=A
Definicja macierzy antysymetrycznej:
Macierz kwadratową A stopnia n, dla której zachodzi warunek: AT=-A nazywamy macierzą antysymetryczną (lub skośnie symetryczną).
Przykład: Macierz antysymetryczna:
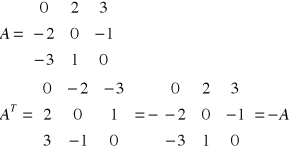
FAKT: Własności macierzy symetrycznej i antysymetrycznej:
Niech A będzie macierzą kwadratową. Wówczas:
macierz A+AT jest symetryczna
macierz A-AT jest antysymetryczna
Niech A będzie macierzą dowolnego wymiaru. Wówczas macierze AAT i ATA są symetryczne.
Każdą macierz kwadratową można jednoznacznie przedstawić w postaci sumy macierzy symetrycznej i antysymetrycznej. Wówczas zachodzi:
![]()
WYZNACZNIKI
Niech dana będzie macierz kwadratowa A=[aij] stopnia n postaci:
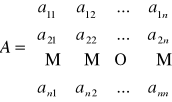
Definicja indukcyjna wyznacznika macierzy:
Wyznacznikiem macierzy kwadratowej nazywamy funkcję, które każdej macierzy rzeczywistej A=[aij] przypisuje liczbę rzeczywistą, ozn. detA , w sposób następujący:
jeżeli macierz A ma stopień n=1, to: detA=a11
jeżeli macierz A ma stopień n>2, to:
detA=a11detA11-a12detA12+a13detA13-...+(-1)1+na1ndetA1n
gdzie Aij oznacza macierz stopnia n-1 otrzymaną z macierzy A przez skreślenie i-tego wiersza i j-tej kolumny.
UWAGA: Wyznacznik macierzy A oznaczamy także symbolem det[aij] lub |A|, a w formie rozwiniętej przez:
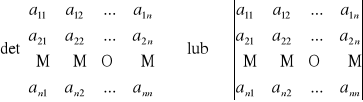
Przykład: Obliczyć:
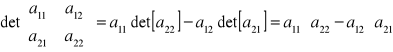
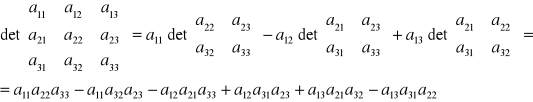
SCHEMAT OBLICZANA WYZNACZNIKA STOPNIA DRUGIEGO:
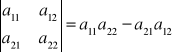
SCHEMAT OBLICZANIA WYZNACZNIKA STOPNIA TRZECIEGO - METODA SARUSA:
1)
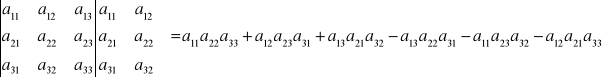
2)
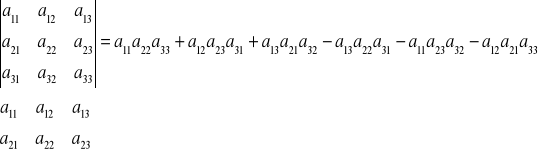
Przykład: Obliczyć wyznaczniki:
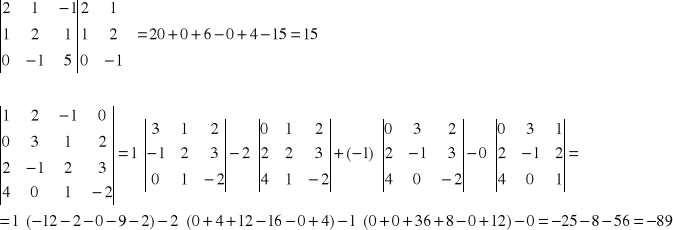
UWAGA: Korzystając z definicji wyznacznika macierzy łatwo można pokazać, że:
detI=1, dla macierzy jednostkowej I dowolnego stopnia
det[diag(a11, a22, a33,...,ann)]=a11∙a22∙a33∙...∙ann
Definicja minora macierzy:
Minorem Mij, stopnia n-1 macierzy kwadratowej A (lub wyznacznika detA) odpowiadającym elementowi aij nazywamy wyznacznik macierzy stopnia n-1, która powstała z macierzy A, w której wykreślono i-ty wiersz i j-tą kolumnę.
Definicja dopełnienia algebraicznego:
Liczbę Aij=(-1)i+jMij, gdzie Mij jest minorem stopnia n-1 macierzy kwadratowej A odpowiadającym elementowi aij, nazywamy dopełnieniem algebraicznym elementu aij.
Twierdzenie Laplace'a o rozwinięciu wyznacznika:
Niech A=[aij] będzie macierzą kwadratową stopnia n>2. Wówczas wyznacznik macierzy A jest równy sumie iloczynów elementów dowolnego wiersza (kolumny) przez ich dopełnienia algebraiczne, tj.:
detA=ai1Ai1+ai2Ai2+ai3Ai3+...+ainAin , przy dowolnie ustalonym i, takim że 1<i<n
oraz
detA=a1jA1j+a2jA2j+a3jA3j+...+anjAnj , przy dowolnie ustalonym j, takim że 1<j<n
Wzór 1) nazywamy rozwinięciem Laplace'a względem i-tego wiersza
2) nazywamy rozwinięciem Laplace'a względem j-tej kolumny
Przykład: Obliczyć:
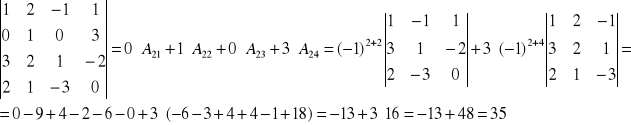
FAKT: Wyznacznik macierzy trójkątnej:
Wyznacznik macierzy trójkątnej dolnej lub górnej jest równy iloczynowi elementów na jego głównej przekątnej, tj.:
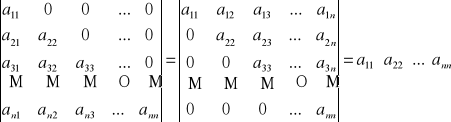
Twierdzenie Cauchy'ego:
Wyznacznik iloczynu macierzy kwadratowych tego samego stopnia jest równy iloczynowi wyznaczników tych macierzy, tj.:
det(AB)=detA∙detB
WNIOSEK: Jeśli A jest macierzą kwadratową i n![]()
N, to det(A)n=(detA)n.
WŁASNOŚCI WYZNACZNIKÓW:
Własność 1: Wyznacznik macierzy kwadratowej mającej kolumnę (wiersz) złożoną z samych zer
jest równy zero.
Własność 2: Wyznacznik macierzy kwadratowej zmieni znak na przeciwny, jeżeli zamienimy ze
sobą dwa wiersze lub dwie kolumny.
Własność 3: Wyznacznik macierzy kwadratowej mającej dwie jednakowe kolumny (dwa
jednakowe wiersze) jest równy zero.
Własność 4: Jeżeli wszystkie elementy pewnej kolumny (pewnego wiersza) macierzy
kwadratowej zawierają wspólny czynnik, to czynnik ten można wyłączyć przed wyznacznik tej macierzy.
Przykład:
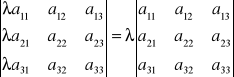
Własność 5: Jeżeli w wyznaczniku elementy pewnej kolumny (pewnego wiersza) są
proporcjonalne do odpowiednich elementów innej kolumny (innego wiersza) to
wyznacznik tej macierzy jest równy zero.
Własność 6: Wyznacznik macierzy kwadratowej, w której elementy pewnej kolumny (pewnego
wiersza) są sumami dwóch składników jest równy sumie wyznaczników macierzy, w których elementy tej kolumny (tego wiersza) są zastąpione tymi składnikami.
Własność 7: Wyznacznik macierzy nie zmieni się, jeżeli do elementów dowolnej kolumny
(dowolnego wiersza) dodamy odpowiadające im elementy innej kolumny (innego wiersza) pomnożone przez dowolną liczbę.
Własność 8: Wyznacznik macierzy jest równy wyznacznikowi macierzy do niej transponowanej.
Przykład: Obliczyć:
MACIERZ ODWROTNA
Definicja macierzy odwrotnej:
Niech A będzie macierzą kwadratową stopnia n. Macierzą odwrotną do macierzy A nazywamy macierz, oznaczoną przez A-1, spełniającą warunek:
AA-1=A-1A=In
gdzie In jest macierzą jednostkową stopnia n.
Definicja macierzy odwracalnej:
Macierz kwadratową posiadającą macierz odwrotną nazywamy macierzą odwracalną.
Definicja macierzy dołączonej:
Macierzą dołączoną do macierzy kwadratowej A (lub macierzą dopełnień algebraicznych) nazywamy macierz oznaczoną przez AD, powstającą z macierzy AT przez zastąpienie w niej każdego elementu aij, odpowiadającym mu dopełnieniem algebraicznym Aij.
Twierdzenie:
Dla dowolnej macierzy kwadratowej A i odpowiadającej jej macierzy dołączonej AD zachodzi:
AAD=ADA=IdetA
Definicja macierzy osobliwej i nieosobliwej:
Macierz kwadratową A nazywamy macierzą osobliwą, jeśli
detA=0
W przeciwnym wypadku (tzn. detA![]()
0) mówimy, że macierz A jest nieosobliwa.
Twierdzenie o wyznaczniku macierzy odwrotnej:
Jeżeli macierz A stopnia n jest nieosobliwa, to zachodzi wzór:
![]()
Przykład: Wyznaczyć macierz odwrotną do 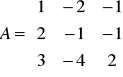
, o ile istnieje.
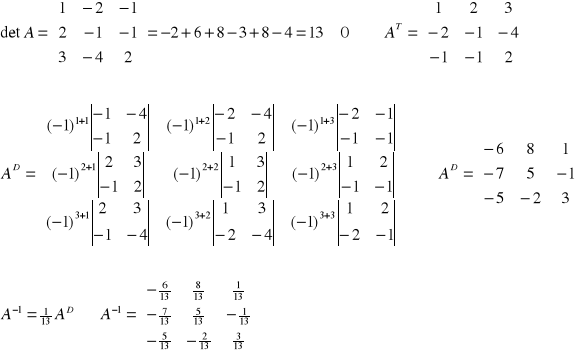
FAKT: Własności macierzy odwrotnych:
Niech macierze A i B tego samego stopnia będą odwracalne oraz niech α![]()
R\{0}, n![]()
N. Wtedy macierze A-1, AT, AB, αA, An także są odwracalne i zachodzą równości:
det(A-1)=(detA)-1
(A-1)-1=A
(AT)-1=(A-1)T
(AB)-1=B-1A-1 !!!
(αA)-1=![]()
(A-1)
(An)-1=(A-1)n
Rozwiązywanie równań macierzowych:
Korzystając z macierzy odwrotnych można w szczególności rozwiązywać równania macierzowe, tj. równania, w których niewiadomą jest macierz X.
Przykład: Wyznaczy macierz X z równania AX+2X=B, gdzie macierz A=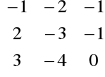
, B=![]()
.
AX+2X=B
(A+2E)X=B, sprawdzić czy A+2E jest odwracalna, tj. det(A+2E)![]()
0.
element neutralny
(macierz jednostkowa)
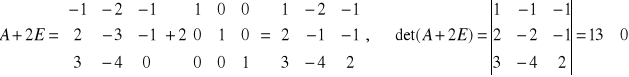
(A+2E)-1∙\(A+2E)=(A+2E)-1B
(A+2E)-1(A+2E)=(A+2E)-1B
EX
EX=(A+2E)-1B
X=(A+2E)-1B
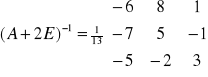
(z poprzedniego przykładu)
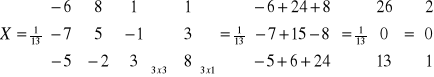
RZĄD MACIERZY
Weźmy dowolną macierz A o wymiarze mxn.
Definicja rzędu macierzy:
Rzędem macierzy nazywamy liczbę r taką, że istnieje minor stopnia r różny od zera, natomiast wszystkie minory stopnia r+1, jakie istnieją w danej macierzy są równe zero. Przyjmujemy dodatkowo, że rząd macierzy zerowej jest równy zero. Rząd macierzy oznaczamy symbolem R(A).
WNIOSEK: Rząd macierzy A jest liczbą całkowitą taką, że 0<R(A)<min(m,n).
WNIOSEK: Dla macierzy kwadratowej A stopnia n nieosobliwej R(A)=n.
Dla macierzy kwadratowej A stopnia n osobliwej R(A)<n.
Przykład: Obliczyć rzędy macierzy A, B i C:
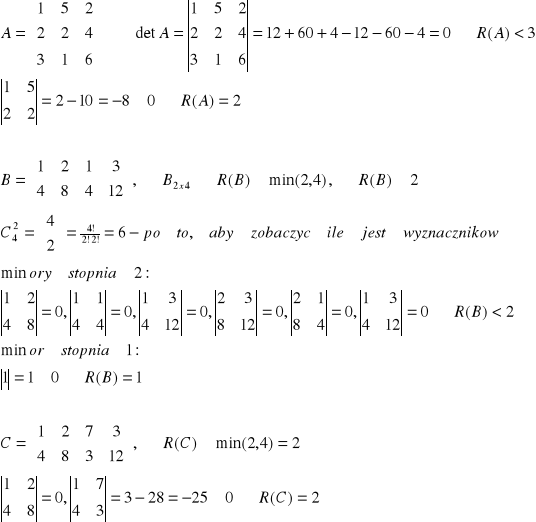
Definicja przekształceń elementarnych:
Przekształceniami elementarnymi macierzy nazywamy:
przestawienie dwóch wierszy (kolumn)
pomnożenie wiersza (kolumny) przez liczbę różną od zera
pomnożenie wiersza (kolumny) przez liczbę i dodanie go do innego wiersza (kolumny).
Twierdzenie:
Przekształcenia elementarne macierzy nie zmieniają rzędu tej macierzy. Rząd macierzy nie zmienia się przy dopisaniu lub skreśleniu z macierzy wiersza (lub kolumny) złożonego z samych zer.
Przykład: Obliczyć rząd macierzy:
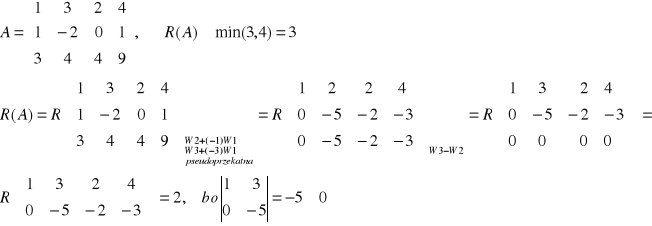
UKŁADY RÓWNAŃ LINIOWYCH
Definicja:
Układem m równań liniowych z n niewiadomymi x1, x2, x3,..., xn, gdzie m, n![]()
N, nazywamy układ równań postaci:
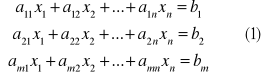
gdzie aij![]()
R, bi![]()
R dla 1<i<m, oraz 1<j<n.
Ponadto:
aij nazywamy współczynnikami układu równań
bi nazywamy wyrazami wolnymi
xj nazywamy niewiadomymi
i=1,2,...,m ; j=1,2,...,n
Rozwiązaniem układu równań liniowych (1) nazywamy układ liczb rzeczywistych x1, x2, x3,..., xn które spełniają każde równanie tego układu.
Układ równań, który nie ma rozwiązań nazywamy układem sprzecznym.
Definicja:
Układ równań (1) nazywamy układem jednorodnym, gdy b1=b2=...=bm=0, natomiast układem niejednorodnym w przypadku przeciwnym.
Definicja:
Rozwiązanie układu równań (1) nazywamy zerowym, gdy: x1=x2=...=xn=0.
UWAGA: Rozwiązanie zerowe jest zawsze jednym z rozwiązań układu jednorodnego.
Metoda macierzowa rozwiązywania układów równań:
Przyjmijmy następujące oznaczenia:
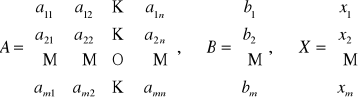
A nazywamy macierzą współczynników układu równań (macierzą układu)
B nazywamy macierzą wyrazów wolnych (wektorem wyrazów wolnych)
X nazywamy macierzą niewiadomych (wektorem niewiadomych)
Przy tak przyjętych oznaczeniach układ równań (1) można zapisać w postaci równania macierzowego: AX=B nazywanego postacią macierzową układy równań.
Przykład:
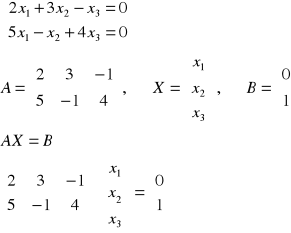
W przypadku, kiedy m=n (układ ma tyle samo rozwiązań co niewiadomych) można stosować tzw. metodę macierzową rozwiązywania układów równań, o ile macierz układu A jest macierzą nieosobliwą. Przy takim założeniu istnieje macierz odwrotna do A, tj.: A-1. W wyniku lewostronnego pomnożenia obu stron równania AX=B przez A-1 otrzymujemy poszukiwane rozwiązanie: X=A-1B.
Przykład: Metodą macierzową rozwiązać układ równań (o ile to możliwe).
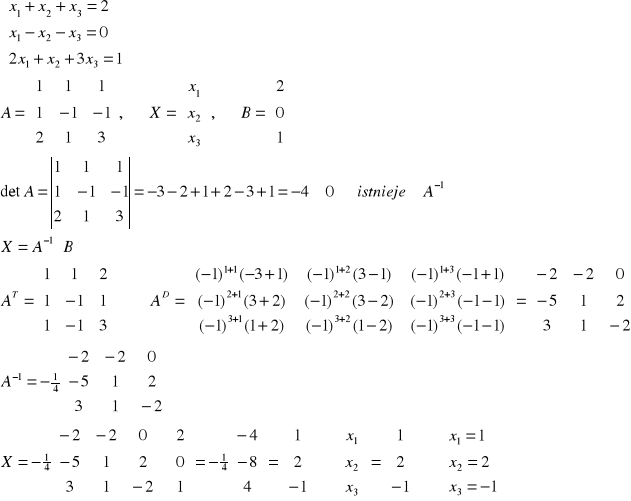
WZORY CRAMERA
Definicja układu Cramera:
Układ równań liniowych:
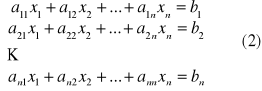
w którym macierz A układu jest macierzą kwadratową nieosobliwą nazywamy układem Cramera.
Twierdzenie Cramera:
Układ Cramera (2) ma dokładnie jedno rozwiązanie. Rozwiązanie to określone jest wzorami:
![]()
gdzie W oznacza wyznacznik macierzy A, natomiast Wi, i=1,2,...,n oznacza wyznacznik macierzy, która powstała z macierzy A przez zastąpienie w niej i-tej kolumny kolumną wyrazów wolnych bi, i=1,2,...,n. Wzory w ramce nazywamy wzorami Cramera.
Przykład: Rozwiązać układ równań:

WNIOSEK: Jednorodny układ Cramera ma tylko jedno rozwiązanie zerowe, tzn.: x1=x2=...=xn=0.
Przykład:
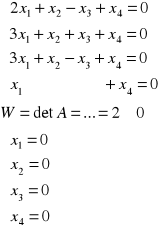
Rozpatrzmy ponownie układ m równań liniowych z n niewiadomymi postaci:
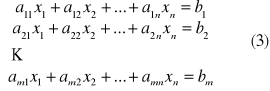
Definicja macierzy rozszerzonej:
Macierzą rozszerzoną nazywamy macierz C powstałą z macierzy A przez dołączenie do niej kolumny wyrazów wolnych, tj. macierz postaci:
Twierdzenie Kroneckera - Capelliego:
Układ równań (3) posiada rozwiązanie wtedy i tylko wtedy, gdy rząd macierz A jest równy rzędowi macierzy rozszerzonej, tj. R(A)=R(C). Jeżeli ponadto R(A)=R(C)=n, to układ równań (3) ma dokładnie jedno rozwiązanie, natomiast R(A)=R(C)=r<n, to układ (3) posiada nieskończenie wiele rozwiązań zależnych od n - r parametrów.
WNIOSEK: Jeżeli R(A)![]()
R(C), to układ równań (3) nie ma rozwiązań.
WNIOSEK: Układ jednorodny ma zawsze rozwiązanie.
Przykład: Rozwiązać układ równań:
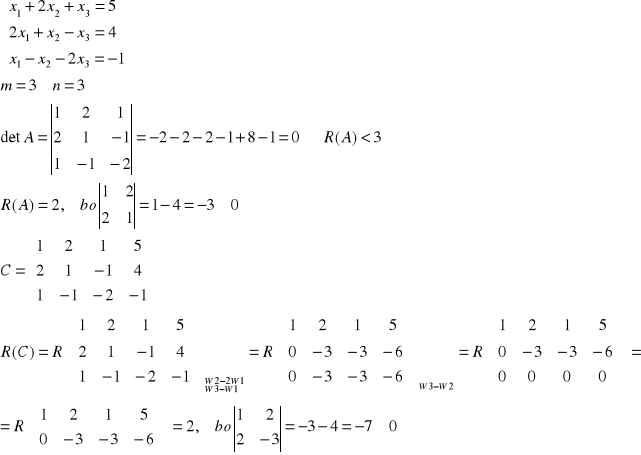
R(A)=R(C)=2<n=3 ![]()
układ ma rozwiązanie
ma nieskończenie wiele rozwiązań zależnych od n-r=3-2=1 parametru
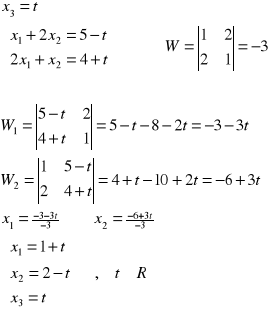
Przykład: Rozwiązać układ równań:
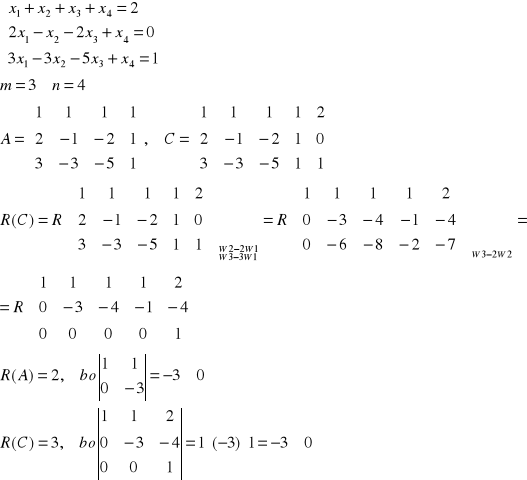
R(A)![]()
R(C) - układ jest sprzeczny - nie ma rozwiązań
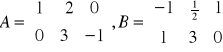
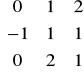
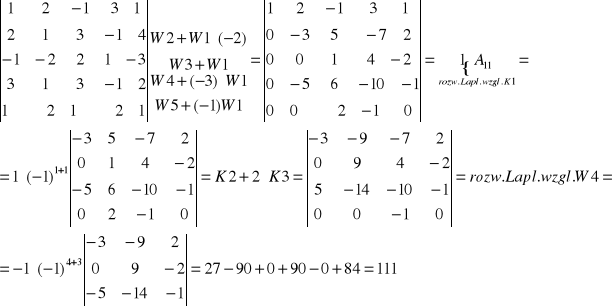
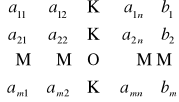
Wyszukiwarka
Podobne podstrony:
Zestaw 12 Macierz odwrotna, układy równań liniowych
W2 RZAD MACIERZY UKLADY ROWNAN LINIOWYCH, UEP lata 2014-2019, Ekonometria
LISTA 10, Macierze i układy równań liniowych
Arkusz zadan Macierze i uklady rownan liniow (2)
MACIERZE UKLADY ROWNAN LINIOWYCH
Zestaw 12 Macierz odwrotna, układy równań liniowych
lab8 1 uklady rownan liniowych
Układy równań liniowych
2011 lab 02, Uklady rownan liniowych
Układy równań liniowych
układy równań liniowych 2
Układy równań liniowych z parametrem
Matematyka I (Ćw) Lista 05 Układy m równań liniowych z n niewiadomymi
Układy równań liniowych, Matematyka dla ekonomistów
Uklady rownan liniowych
02. Układy równań liniowych
2011 lab 02 Uklady rownan liniowychid 27450
więcej podobnych podstron