UKŁADY 

RÓWNAŃ 

LINIOWYCH

Z

PARAMETREM

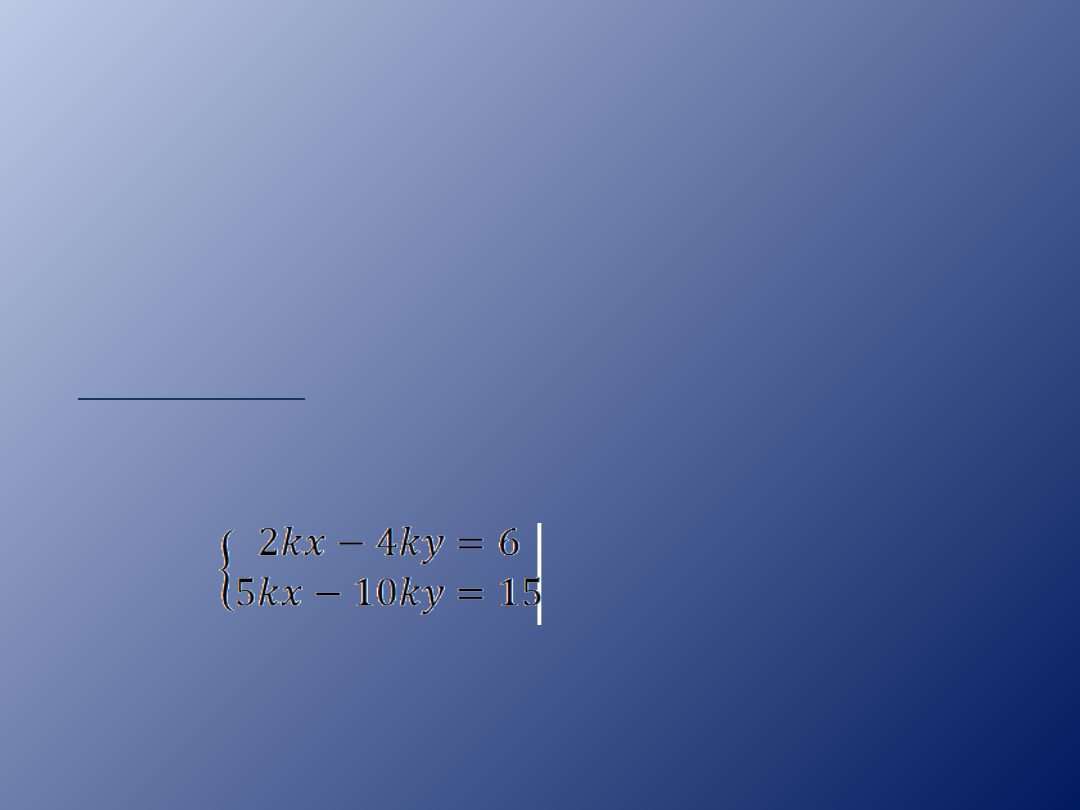
Zajmiemy się rozwiązaniem układu równań 

z PARAMETREM. Parametr to dowolna liczba 

rzeczywista, od której zależy liczba rozwiązań 

układu równań. 

Przykład 1.
Rozwiąż układ równań w zależności od 
parametru k.

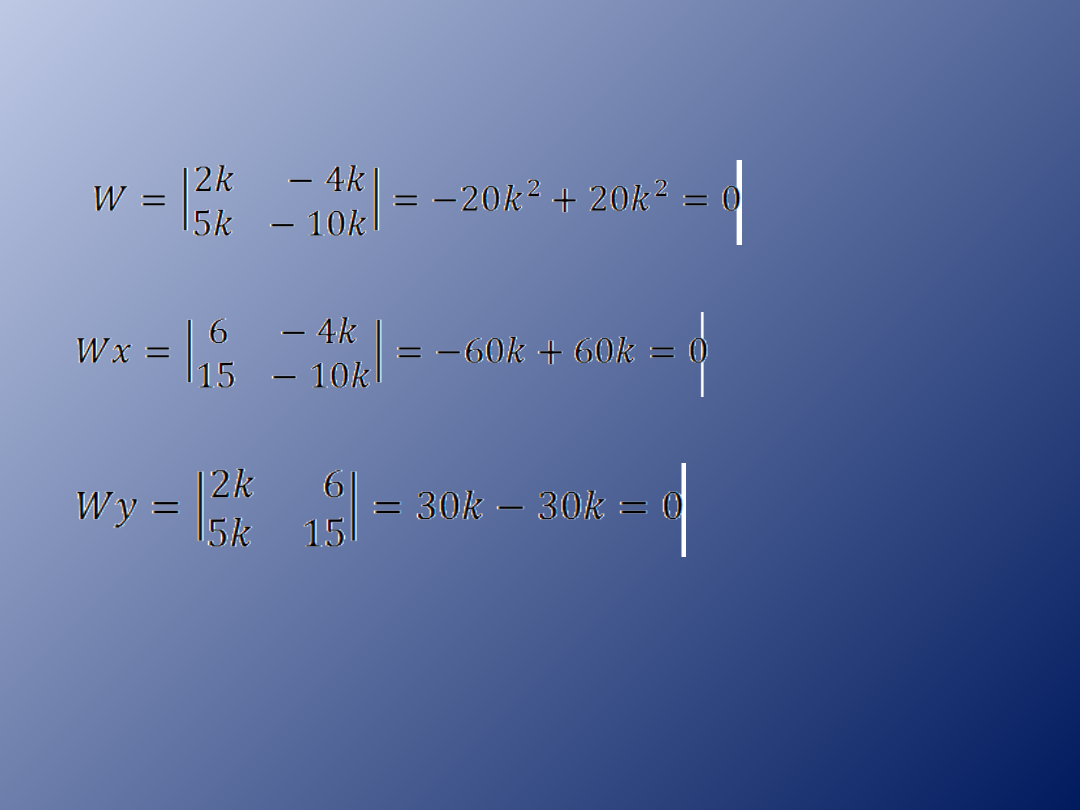
Obliczamy wyznaczniki dla układu równań.

W=Wx=Wy=0 

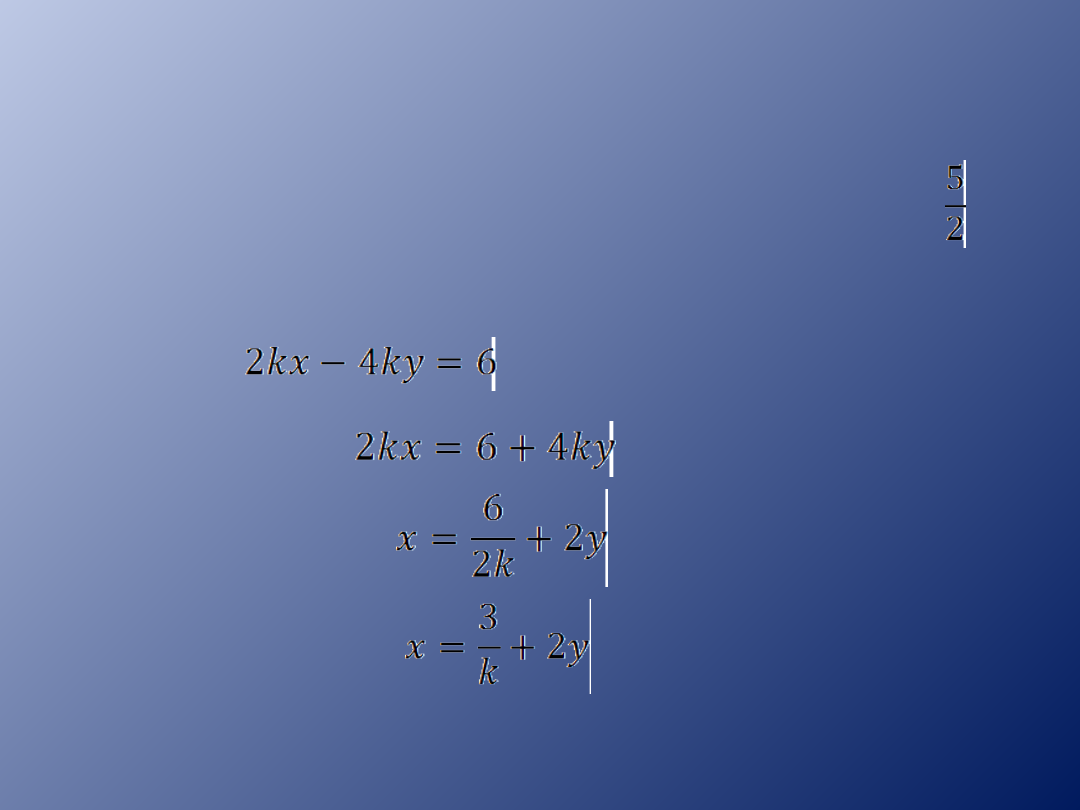
Układ równań jest równoważny jednemu z 

tych równań (np. drugie równanie 

otrzymujemy przez pomnożenie obu stron 

pierwszego równania przez

Wystarczy rozważyć jedno równanie, np. 

pierwsze. 

Dla k ≠ 0  podstawiając za y dowolną liczbę 

rzeczywistą otrzymujemy nieskończenie wiele 

rozwiązań.

Układ równań wtedy ma nieskończenie wiele 

rozwiązań (układ nieoznaczony).

Dla k = 0 otrzymujemy równanie: 

Jest to równanie nieprawdziwe. Układ równań 

jest sprzeczny.

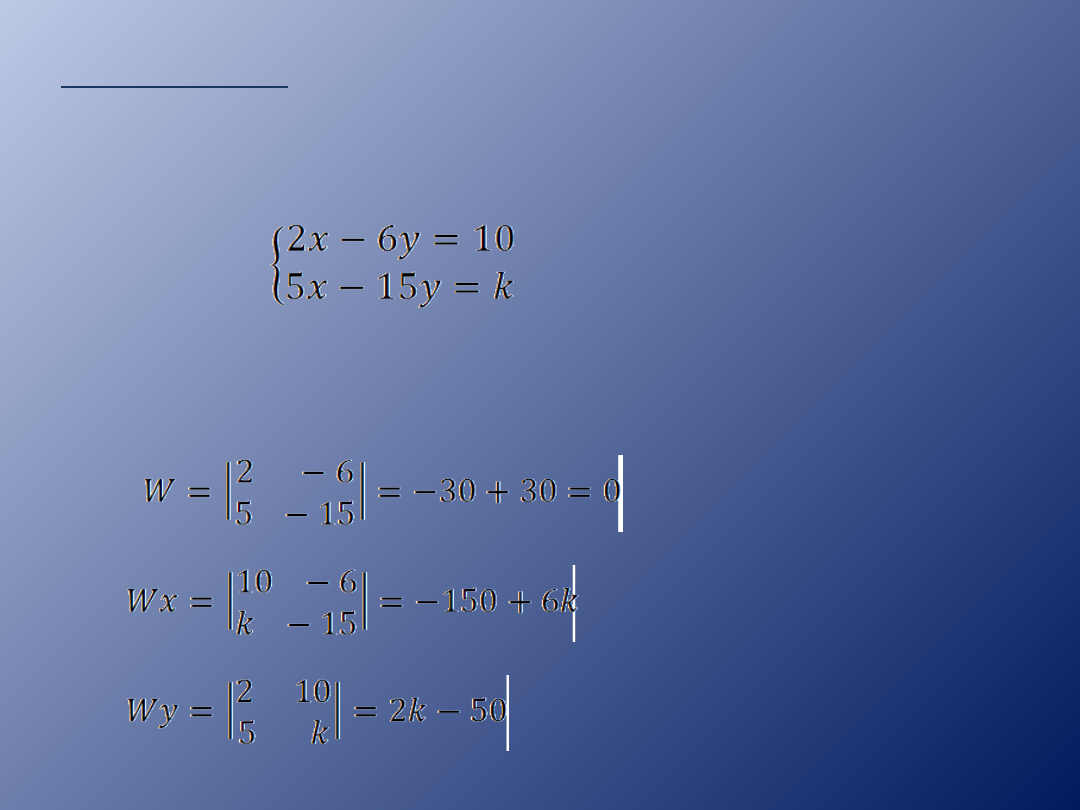
Przykład 2.
Zbadaj liczbę rozwiązań układu równań w 
zależności od parametru k.

Obliczamy wyznaczniki.

Wyznacznik W = 0 więc układ albo ma 

nieskończenie wiele rozwiązań albo nie ma 

wcale.

Rozważyć musimy dwa przypadki:

PRZYPADEK 1.

Układ ma nieskończenie wiele rozwiązań 

jeżeli:

     Wx = 0      i      Wy = 0

-150+6k=0           2k-50=0

       6k=150            2k=50

        k=25               k=25

Dla k=25 układ równań ma nieskończenie 

wiele rozwiązań. 

PRZYPADEK 2.

Układ nie ma rozwiązań jeżeli:

     Wx ≠ 0      lub      Wy ≠ 0

-150+6k ≠ 0           2k-50 ≠ 0

       6k ≠ 150            2k ≠ 50

        k ≠ 25               k ≠ 25

Dla k ≠ 25 układ równań nie ma rozwiązań, 

jest sprzeczny.

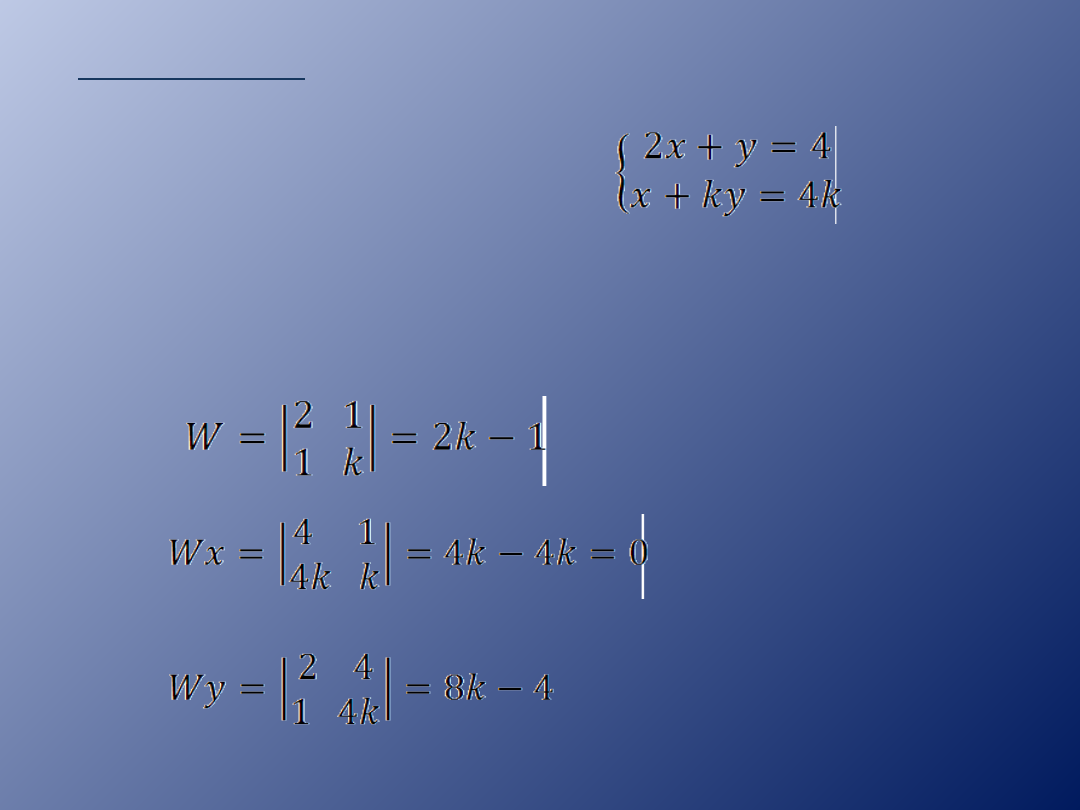
Przykład 3.
Dla jakiej wartości 
parametru k układ 
równań jest 
nieoznaczony?

Obliczamy 
wyznaczniki.

Układ jest nieoznaczony gdy spełnione są 

warunki:

    W=0      i        Wx=0      i        Wy=0

  2k–1=0                k∈R              8k-4=0

    2k=1                                     8k=4

     k=0,5                                     k=0,5

Dla k=0,5 układ równań ma nieskończenie 

wiele rozwiązań (jest nieoznaczony). 

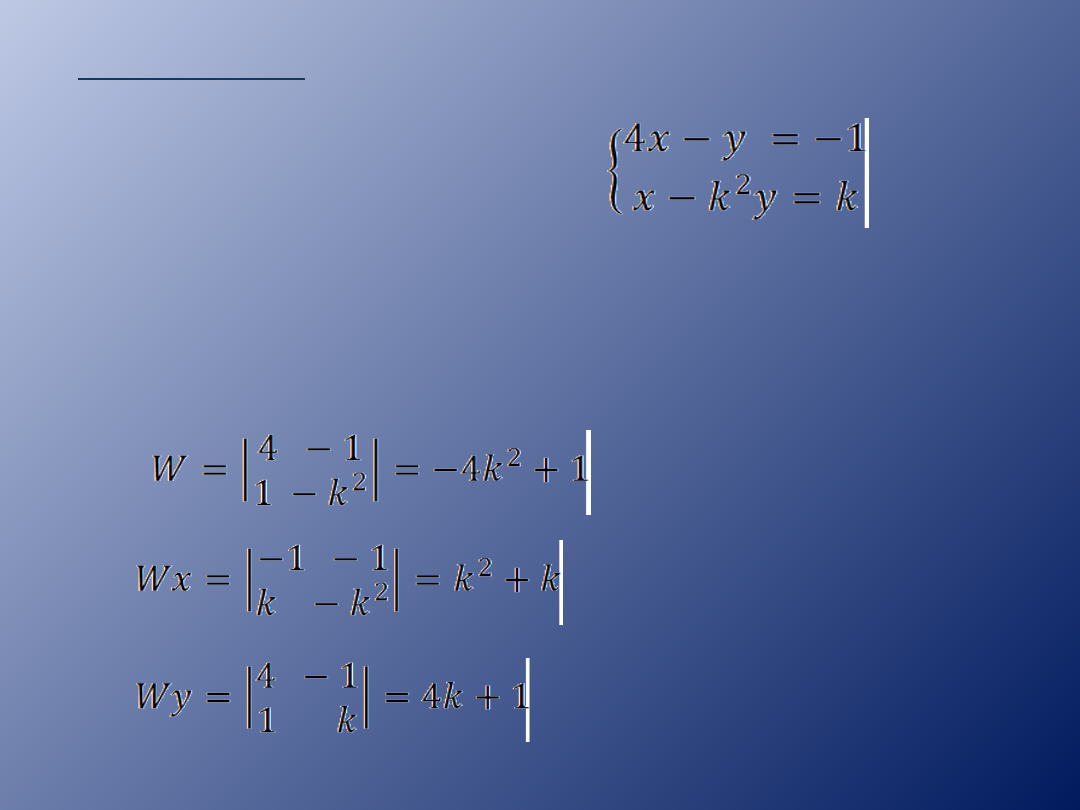
Przykład 4.
Dla jakiej wartości 
parametru k układ 
równań jest 
oznaczony?

Obliczamy 
wyznaczniki.

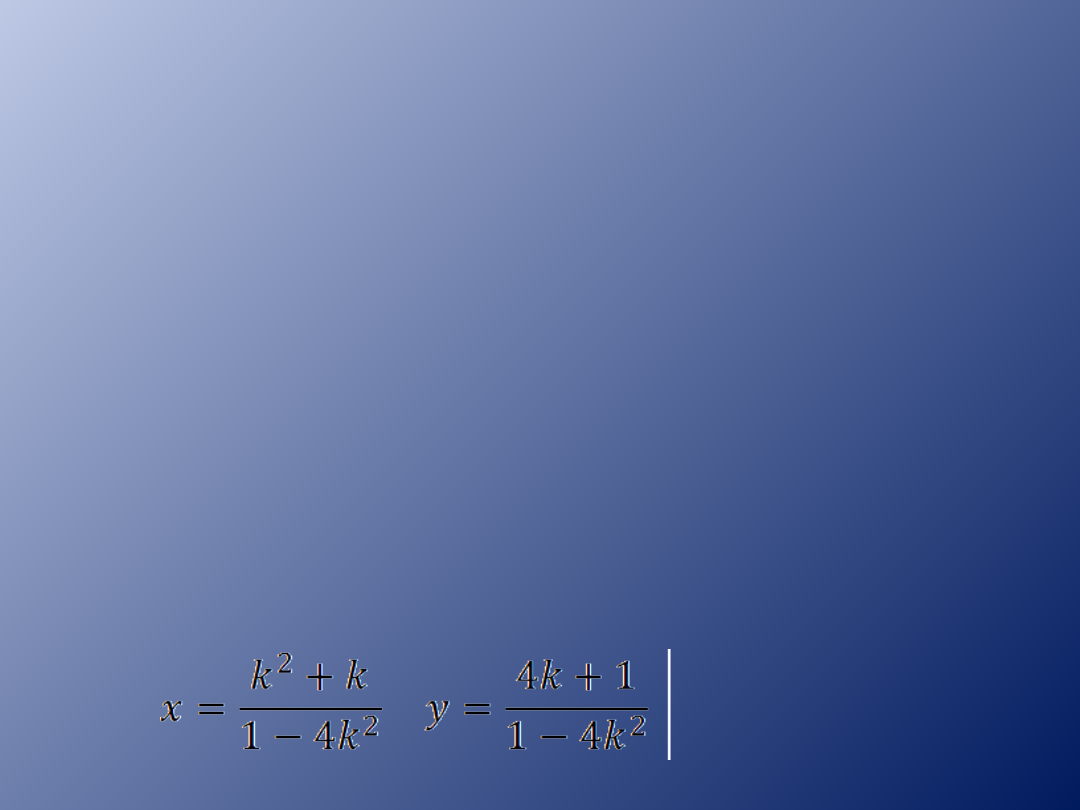
Układ równań jest oznaczony gdy spełniony 
jest warunek:

              W ≠ 0 

         -4k

2

+1 ≠ 0

            -4k

2 

≠ -1

              4k

2 

≠ 1

               k

2 

≠ ¼

                k ≠ ½        i       k ≠ -½ 

Dla k ∈ R\{- ½; ½ } układ równań ma jedno 

rozwiązanie. 

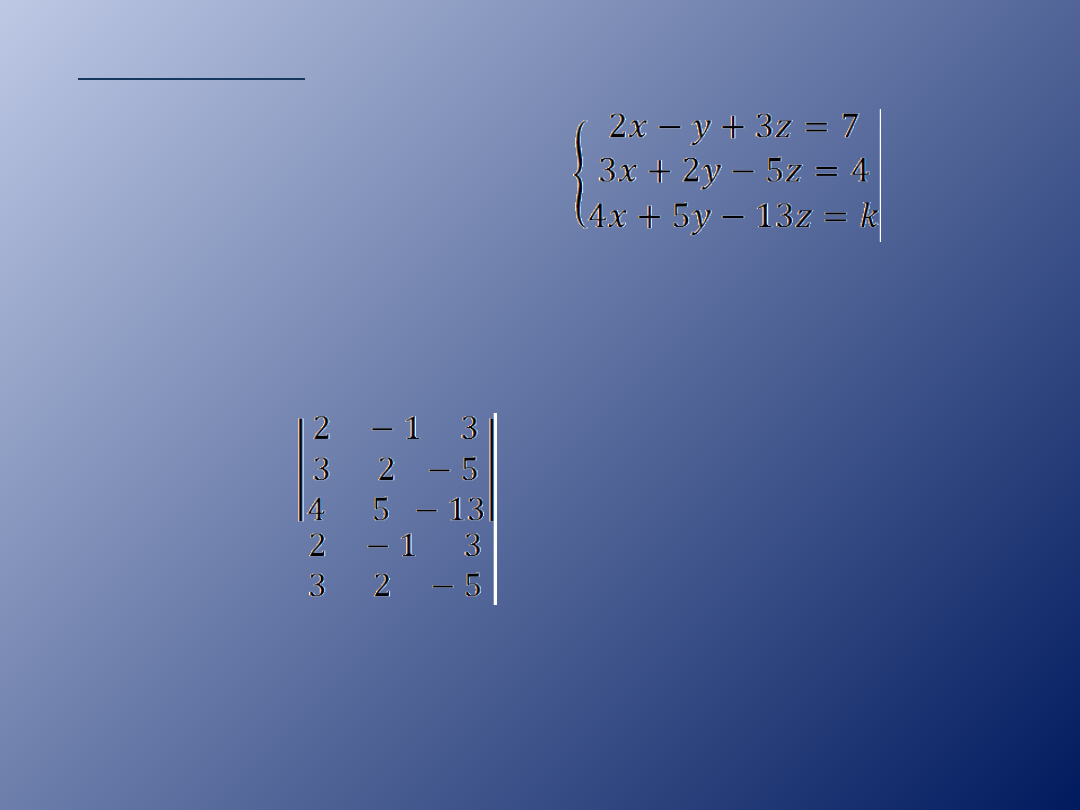
Przykład 5.
Dla jakiej wartości 
parametru k układ 
równań jest 
sprzeczny?.

W=                      

W = -52+45+20-24+50-39 = 0

Obliczamy wyznacznik W oraz wyznaczniki: 
Wx, Wy, Wz.

Wx = -182+60+5k-6k+175-52=1-k

Wx =

Wy =

Wy = -104+9k-140-48+10k+273=19k-19

Wz = 4k+105-16-56-40+3k=7k-7

Wz =

Wyznacznik W ma wartość 0, natomiast 

wyznaczniki Wx, Wy, Wz są zależne od 

parametru k.

Układ równań nie posiada żadnych 

rozwiązań jeżeli: Wx≠0  lub Wy≠0  lub 

Wz≠0.

 
Wx ≠ 0      ∨      Wy ≠ 0        ∨     Wz ≠ 0
1- k ≠ 0        19k-19 ≠ 0             7k-7 ≠ 0
    k ≠ 1                k ≠ 1                                 k 
≠ 1 

Dla k ≠ 1 wszystkie wyznaczniki są różne od 

zera, wtedy układ równań jest sprzeczny.