RZĄD MACIERZY

Mówimy, że macierz A_m×n jest rzędu r, gdzie r≤ min(m,n), jeśli istnieje dla tej macierzy co najmniej jeden minor stopnia r różny od zera, a wszystkie minory stopnia wyższego niż r są równe zero. Rząd macierzy A oznaczamy symbolem rz(A).

Przekształcenia elementarne macierzy zachowujące rząd

• pomnożenie dowolnego wiersza (kolumny) przez liczbę różną od zera

• dodanie do dowolnego wiersza (kolumny) innego wiersza (kolumny) tej macierzy

• zamiana miejscami wierszy (kolumn)

• pominięcie wiersza (kolumny) zerowego

Rząd macierzy jednostkowej stopnia n wynosi n

rz(I_n)=n

Rząd macierzy trójkątnej jest równy liczbie elementów niezerowych leżących na jej głównej przekątnej

W celu wyznaczenia rzędu macierzy dokonuje się ciągu przekształceń elementarnych (równoważnych) na jej wierszach by doprowadzić do jednej z następujących postaci blokowych:

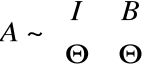
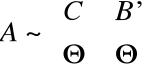
gdzie: I - macierz jednostkowa

C - macierz trójkątna

- macierz zerowa

B, B' - inna macierz

Wówczas:

UKŁADY RÓWNAŃ LINIOWYCH

Dany jest układ m równań liniowych o n niewiadomych:

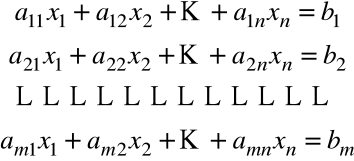
Układ ten może mieć:

• więcej niewiadomych niż równań (n > m),

• niewiadomych tyle samo co równań (n = m),

• mniej niewiadomych niż równań (n < m).

Inny zapis układu równań liniowych:

1. zapis za pomocą znaku sumy

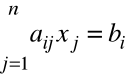
dla i=1, 2, 3, ..., m

2) zapis macierzowy

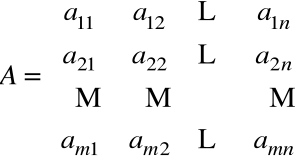
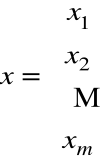
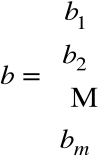
A⋅x=b

gdzie: A - macierz współczynników układu równań

x - wektor niewiadomych

b - wektor wyrazów wolnych (prawa strona układu)

Macierz A z dołączoną kolumną b nazywać będziemy macierzą uzupełnioną (rozszerzoną) i oznaczać symbolem U, tzn.

Układ równań liniowych nazywamy

1. oznaczonym - jeśli posiada dokładnie jedno rozwiązanie

2. nieoznaczonym - jeśli posiada nieskończenie wiele rozwiązań

3. sprzeczny - jeśli nie posiada rozwiązań

Przez rozwiązanie układu równań rozumiemy wektor x, którego składowe spełniają jednocześnie wszystkie równania układu.

Twierdzenie Kroneckera-Capelli'ego

Układ m równań liniowych o n niewiadomych posiada rozwiązanie wtedy i tylko wtedy, gdy rząd macierzy układu jest równy rzędowi macierzy uzupełnionej, tzn.

rz A = rz U = r

Ponadto, jeśli:

r = rz A ≠ rz U to układ jest sprzeczny

r = rz A = rz U = n to układ jest oznaczony

r = rz A = rz U < n to układ jest nieoznaczony i posiada
nieskończenie wiele rozwiązań
zależnych od n - r parametrów

Przykład

a) Dany jest układ równań

.

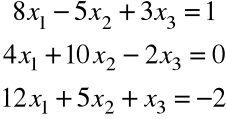
Macierz współczynników przy niewiadomych jest postaci

,

natomiast macierzą uzupełnioną jest macierz

.

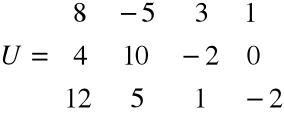
Ponieważ rz A = 2, a rz U = 3 (sprawdzić), czyli rz A < rz U, więc układ jest sprzeczny, a zatem nie ma rozwiązań.

b) Dany jest układ równań

.

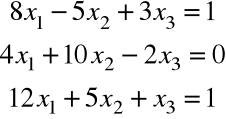
Macierz współczynników przy niewiadomych jest taka sama jak w przykładzie a), natomiast macierzą uzupełnioną jest macierz

.

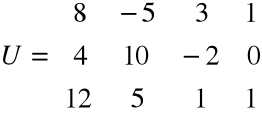
Ponieważ rz A = 2 = rz U = 2 < 3 (sprawdzić), więc układ jest nieoznaczony i ma nieskończenie wiele rozwiązań zależnych od n - r = 3 - 2 = 1, czyli jednego parametru.

c) Dany jest układ równań

.

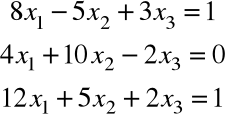
Macierz współczynników przy niewiadomych jest postaci

natomiast macierzą uzupełnioną jest macierz

.

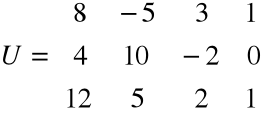
Ponieważ rz A = rz U = n = 3 (sprawdzić), więc układ jest oznaczony i ma dokładnie jedno rozwiązanie.

Układ m równań liniowych o n niewiadomych nazywamy układem jednorodnym, jeśli wektor wyrazów wolnych jest wektorem zerowym, tzn. Ax=θ.

Układ jednorodny jest układem niesprzecznym i zawsze posiada przynajmniej jedno rozwiązanie zerowe. Rozwiązanie zerowe układu jednorodnego nazywamy rozwiązaniem trywialnym.

Układ jednorodny posiada rozwiązanie nietrywialne wtedy i tylko wtedy, gdy rz A < n.

Układ n równań o n niewiadomych nazywamy układem Cramera, jeżeli macierz układu jest nieosobliwa (detA≠0)

Układ Cramera postaci A⋅x=b jest układem oznaczonym, a rozwiązanie takiego układu można otrzymać za pomocą:

(a) macierzy odwrotnej, wtedy

x=A^-1⋅ b

(b) wzorów Cramera, wtedy

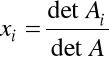
gdzie
jest macierzą powstałą z macierzy
przez zastąpienie i-tej kolumny kolumną wyrazów wolnych.

Przykład

Rozwiązać następujący układ równań za pomocą

1. wzorów Cramera,

2. macierzy odwrotnej.

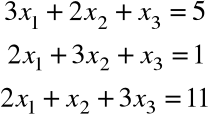
Ad (a). Obliczamy wyznacznik macierzy współczynników

.

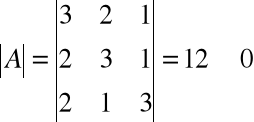
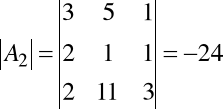
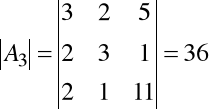
Dany układ jest układem Cramera. Obliczamy wyznaczniki macierzy A₁, A₂ i A₃. Mamy

,
,
.

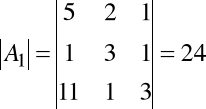
Zatem według wzorów Cramera

,
,
.

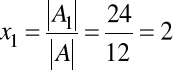
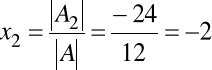
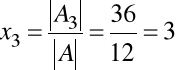
Rozwiązanie układu: x₁=2, x₂=-2, x₃=3

Ad (b). Szukamy rozwiązania za pomocą
.

Wyznacznik macierzy A wynosi 12. Wyznaczamy macierz odwrotną

.

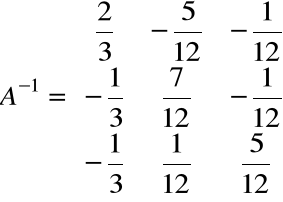
I ostatecznie mamy

.

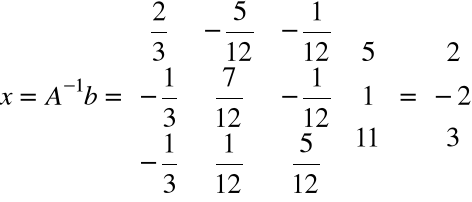
Uwaga!

Poprawność rozwiązania można sprawdzić podstawiając uzyskane wartości do wyjściowego układu.

Dla układu Ax=b, gdzie rzA=rzB=r istnieje macierz A' stopnia r, że detA'≠ 0. Przekształcając układ równań Ax=b do takiej postaci, że współczynniki przy niewiadomych są elementami macierzy A' doprowadzamy układ wyjściowy do postaci nazywanej układem zredukowanym. Rozwiązanie układu zredukowanego (równoważnego) jest rozwiązaniem układu wyjściowego.

METODY ROZWIĄZYWANIA DOWOLNYCH
UKŁADÓW RÓWNAŃ LINIOWYCH

Dwa układy równań liniowych
oraz
nazywamy układami równoważnymi wtedy i tylko wtedy, gdy
tzn. jeżeli jeden z nich można przekształcić do postaci drugiego za pomocą przekształceń elementarnych.

Twierdzenie o układach równoważnych

Układy równoważne mają identyczne zbiory rozwiązań.

Metoda Gaussa

(metoda przekształceń elementarnych)

Dany jest układ m równań o n niewiadomych

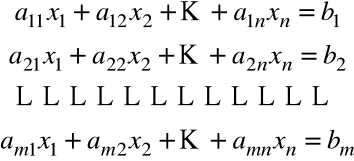
(6)

Utwórzmy macierz uzupełnioną powyższego układu

,

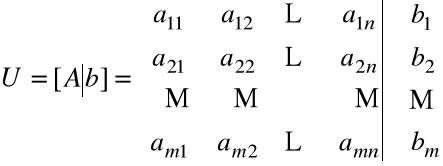
przy czym pionową kreską oddzielono wyrazy wolne od współczynników przy niewiadomych.

Porównując przekształcenia elementarne na wierszach macierzy U i równaniach układu równań zauważamy:

1. Pomnożenie obu stron równania układu przez dowolną liczbę różną od zera jest równoważne
   z pomnożeniem wszystkich elementów odpowiedniego wiersza macierzy U przez tę samą liczbę.

2. Przestawienie miejscami dwóch równań układu jest równoważne z przestawieniem w macierzy U odpowiednich dwóch jej wierszy.

3. Dodanie stronami do równania układu innego równania tego układu, pomnożonego stronami przez pewną liczbę, jest równoważne z dodaniem do wszystkich elementów odpowiedniego wiersza macierzy uzupełnionej U odpowiadających elementów innego wiersza pomnożonych przez tę samą liczbę.

Wniosek

Przekształcenia elementarne na układzie równań są równoważne odpowiednim przekształceniom elementarnym wykonywanym na wierszach macierzy uzupełnionej danego układu równań.

Układ równań liniowych przekształca się do nowego układu równoważnego wykonując odpowiednie przekształcenia elementarne na wierszach macierzy uzupełnionej tego układu.

[Ab] → [A'b']

Aby rozwiązać dany układ równań lub stwierdzić, czy jest on układem sprzecznym, należy za pomocą przekształceń elementarnych sprowadzić macierz uzupełnioną U do jej postaci kanonicznej.

Przypuśćmy, że postać kanoniczna jest następująca:

.

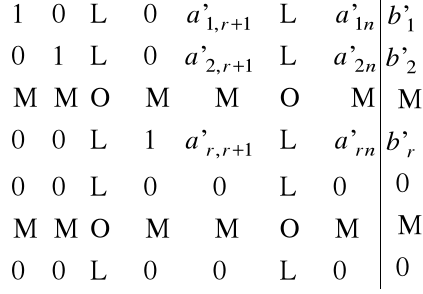
Oznacza to, że układ równań (6) przekształcono do postaci równoważnej

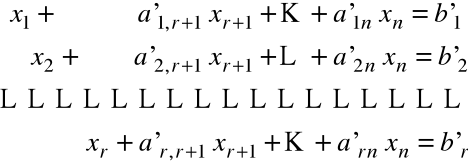
(7)

zwanej postacią kanoniczną lub bazową układu równań (6).

Z postaci kanonicznej macierzy U wynika, że

rz A = rz U = r.

Układ równań (7) nazywamy układem zredukowanym układu (6), ponieważ nie zawiera m - r równań, które są kombinacją liniową r równań niezależnych wchodzących w skład tego układu.

Ponadto, każde ze wspomnianych wyżej m - r równań przekształcone zostało do równania

,

które jest spełnione dla dowolnych wartości niewiadomych i dlatego pomijając takie równania otrzymujemy układ równań (7) równoważny układowi (6).

Zmienne x_r+1, ..., x_n są tzw. zmiennymi swobodnymi (parametrami), od których uzależnione są pozostałe zmienne tzw. zmienne bazowe.

Rodzaje rozwiązań:

Rozwiązaniem ogólnym układu równań liniowych nazywamy takie rozwiązanie układu, w którym niewiadome bazowe są funkcjami niewiadomych swobodnych (niebazowych).

Rozwiązaniem szczególnym układu równań liniowych nazywamy takie rozwiązanie ogólne układu, w którym przyjęto dowolne, lecz ustalone wartości niewiadomych niebazowych.

Rozwiązaniem bazowym układu równań liniowych nazywamy takie rozwiązanie szczególne układu,
w którym przyjęto zerowe wartości niewiadomych niebazowych.

Przykład

Rozwiązać następujące układy równań metodą Gaussa

(a)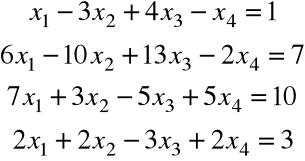

(b)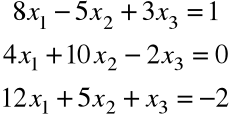
.

2

---