Przyjmujemy następujące oznaczenia:

1. dla zdarzeń

- najwcześniejszy możliwy termin zajścia zdarzenia poprzedzającego,

- najpóźniejszy dopuszczalny termin zajścia zdarzenia poprzedzającego,

- zapas czasu dla zdarzenia

- najwcześniejszy możliwy termin zajścia zdarzenia następującego,

- najpóźniejszy dopuszczalny termin zajścia zdarzenia następującego,

- zapas czasu dla zdarzenia
.

2. dla czynności

- najwcześniejszy możliwy termin rozpoczęcia czynności
,

- najwcześniejszy możliwy termin zakończenia czynności
,

- najpóźniejszy dopuszczalny termin rozpoczęcia czynności
,

- najpóźniejszy dopuszczalny termin zakończenia czynności
.

Terminy rozpoczęcia i zakończenia czynności wylicza się na podstawie następujących wzorów:

(1)

(2)

(3)

(4)

Czynności nieleżące na ścieżce krytycznej nie wpływają na wykonanie całego przedsięwzięcia. Czynności te mają zapas czasu. Wyróżniamy trzy rodzaje zapasów czasu:

1. Zapas całkowity:

(5)

2. Zapas swobodny:

(6)

3. Zapas warunkowy:

(7)

Przy budowie pewnego obiektu można wyróżnić 14 czynności oraz 10 zdarzeń. Czynności oraz czasy ich trwania podano w tabeli. Wyznaczyć ścieżkę krytyczną, określić najkrótszy czas realizacji całego przedsięwzięcia, terminy zdarzeń oraz terminy czynności, zapasy czasu zdarzeń oraz zapasy czasu czynności. Dodatkowo utworzyć model liniowy oraz narysować wykres Gantta.

Tabela 1.

Przedstawienie numeracji zdarzeń

Czynność	Identyfikator czynności	Numer zdarzenia		Czynność	Identyfikator czynności	Numer zdarzenia
						poprzedzającego	następującego			poprzedzającego	następującego
	A	0	1		H	4	5
	B	0	2		I	5	6
	C	1	4		J	5	8
	D	2	4		K	5	7
	E	1	3		L	6	9
	F	3	4		M	8	9
	G	3	5		N	7	9

W Poniższej tabeli przedstawione są czasy trwania poszczególnych czynności. Przyjętą jednostką czasu jest tydzień.

Tabela 2.

Wartości ocen czasów trwania czynności

Identyfikator czynności	Czas trwania zadania	Identyfikator czynności	Czas trwania zadania
A	4	H	2
B	5	I	5
C	8	J	4
D	3	K	3
E	7	L	3
F	0	M	6
G	8	N	5

Na podstawie przyjętych danych należy określić ścieżkę krytyczną oraz czas trwania przedsięwzięcia.

Rozwiązanie:

W poniższej tabeli przedstawiono terminy dla zdarzeń:

Tabela 3.

Terminy dla zdarzeń.

Identyfikator czynności	Czas trwania czynności	Numer zdarzenia		Zdarzenie początkowe			Zdarzenie końcowe
				poprzedzającego	następującego
A	4	0	1	0	0	0	4	4	0
B	5	0	2	0	0	0	5	14	9
C	8	1	4	4	4	0	12	17	5
D	3	2	4	5	14	9	12	17	5
E	7	1	3	4	4	0	11	11	0
F	0	3	4	11	11	0	12	17	5
G	8	3	5	11	11	0	19	19	0
H	2	4	5	12	17	5	19	19	0
I	5	5	6	19	19	0	24	26	2
J	4	5	8	19	19	0	23	23	0
K	3	5	7	19	19	0	22	24	2
L	3	6	9	24	26	2	29	29	0
M	6	8	9	23	23	0	29	29	0
N	5	7	9	22	24	2	29	29	0

Poniżej przedstawiono terminy dla czynności.

Tabela 4.

Terminy dla czynności.

Identyfikator czynności	Czas trwania czynności	Numer zdarzenia		Terminy dla czynności
											Poprzedzającego c	Następującego d
A	4	0	1	0	4	0	4	0	0	0
B	5	0	2	0	5	9	14	9	0	9
C	8	1	4	4	12	9	17	5	0	5
D	3	2	4	5	8	14	17	9	4	0
E	7	1	3	4	11	4	11	0	0	0
F	0	3	4	11	11	17	17	6	1	6
G	8	3	5	11	19	11	19	0	0	0
H	2	4	5	12	14	17	19	5	5	0
I	5	5	6	19	24	21	26	2	0	2
J	4	5	8	19	23	19	23	0	0	0
K	3	5	7	19	22	21	24	2	0	2
L	3	6	9	24	27	26	29	2	2	0
M	6	8	9	23	29	23	29	0	0	0
N	5	7	9	22	27	24	29	2	2	0

Model liniowy:

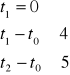
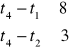
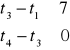
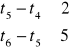
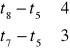
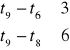
dla każdego

Model ten rozwiązujemy stosując dodatek Solver. W wyniku wykorzystania tego narzędzia otrzymujemy następujące rozwiązanie dla zmiennych t.

Na podstawie otrzymanego rozwiązania można stwierdzić, że czas trwania realizacji tego przedsięwzięcia wynosi 29 dni. W celu określenia ścieżki krytycznej sprawdzamy, dla których ograniczeń otrzymaliśmy status „Wiążący”. Czynności, odpowiadające tym ograniczeniom są potencjalnymi czynnościami krytycznymi. W celu potwierdzenia tego, należy utworzyć sieć z czynności, dla których otrzymano status „Wiążący”. Ścieżkę krytyczną wyznaczają te czynności, które posiadają status „Wiążący” oraz tworzą ciągłą sieć połączeń między zdarzeniami nr. 0 i 9. Na tej podstawie można stwierdzić, że ścieżkę krytyczną tworzą czynności o następujących zdarzeniach 0-1-3-5-8-9 .

---