Skręcanie

1. Oblicz max w skręcanym wsporniku o przekroju teowym, którego półka ma wymiary a x 16a zaś środnik ma wymiary a x 10a (wskazówka: dla prostokąta jest: Mx= GJx , Ix =b3h, max =Mx /Wx , W_x =b2h, można przyjąć: a = = 0.333).

2. Do pręta o przekroju pierścieniowym o średnicy zewn. d i wewn. 0.8d oraz długości l, utwierdzonego na jednym końcu, przyłożono na całej długości moment skręcający o gęstości
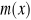
   . Wyprowadź wzory na maksymalny kąt skręcenia. (można przyjąć liniową zależność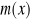
   = a + bx).

3. Rozpisać statyczne warunki brzegowe na pobocznicach (wewnętrznej i zewnętrznej pręta o przekroju rurowym. Wykorzystać te warunki w zagadnieniu Neumanna rządzące rozwiązaniem skręcanego pręta o przekroju rurowym i wykazać, że rozwiązaniem jest funkcja spaczenia tożsamościowo równa zeru.

4. Premia: Narysować rozkład naprężeń w przekroju poprzecznym zad. 3 i wyprowadzić wzór na maksymalne naprężenia styczne.

1. Wyprowadź potrzebny wzór dla obliczenia max w skręcanej belce o przekroju teowym, którego półki i środnik mają wymiary a x 3a, a grubość:
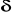
   (wskazówka: dla prostokąta jest: Mx= GJx , Ix =b3h, max =Mx /Wx , W_x =b2h).

2. Napisz lub opisz jak wygląda zagadnienie brzegowe rządzące rozwiązaniem czystego skręcania.

3. Wykonano dwa pręty o identycznej geometrii. Jeden z materiału o wytrzymałości na ścinanie 40 MPa, drugi - 80 MPa. Obydwa skręcono momentem Mx o tej samej wartości. Obliczyć stosunek max naprężeń stycznych.

4. Wykonano dwa pręty o średnicy d. Oba utwierdzone, jeden o długości l drugi - 2l i skręcono momentem Mx. Obliczyć stosunek kątów skręcenia.

5. Do pręta o długości l, utwierdzonego na jednym końcu o średnicy d przyłożono dwa momenty skręcające: na swobodnym końcu
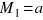
   i w połowie długości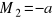
   . Oblicz kąt skręcenia swobodnego przekroju poprzecznego-

6. Do pręta o średnicy d i długości l, utwierdzonego na jednym końcu, przyłożono na całej długości moment skręcający o gęstości
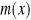
   . Oblicz maksymalny kąt skręcenia.

7. Pokaż tok postępowania przy wyprowadzeniu zagadnienia brzegowego dla funkcji spaczenia
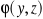
   rządzącego rozwiązaniem czystego skręcania

8. Co nazywamy funkcją spaczenia w przypadku skręcanego pręta? Jak ją wyznaczamy?

9. Wykaż, że funkcja spaczenia dla przekroju kołowego jest tożsamościowo równa zeru.

10. Cienkościenna rura o grubości d, o promieniu linii środkowej r i długości l i przecięta wzdłuż tworzącej, skręcana jest momentem M_x Oblicz wartość maksymalnego naprężenia (wskazówka: dla prostokąta jest:
    )

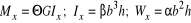
11. Co to jest proste a co czyste skręcanie ? Podaj zależności pomiędzy obciążeniami w obu przypadkach

12. Napisz macierz naprężeń w przypadku prostego skręcania i przeprowadź analizę stanu naprężenia.

13. Zapisz zagadnienie Neumanna rządzące rozwiązaniem skręcanego pręta o przekroju rurowym. Co powiesz o rozwiązaniu?

14. Uzasadnij, na jakiej podstawie możemy na ściance czołowej zastąpić utwierdzenie w punkcie środkowym utwierdzeniem całej ścianki?

15. Wyprowadź wzór określający maksymalne naprężenie styczne dla cienkościennego pręta o jednokomorowym zamkniętym profilu

16. Uzasadnij, na jakiej podstawie możemy na ściance czołowej utwierdzenie w punkcie środkowym zastąpić utwierdzeniem całej ścianki?

17. Jakie dwa stany graniczne leżą u podstaw projektowania skręcanego pręta?. Zdefiniuj oba.

18. Napisz zależność pomiędzy kątem skręcenia pręta i jednostkowym kątem skręcenia.

19. Jaka wielkość opisuje spaczenie przekroju kołowego przy czystym skręcaniu i jak ją wyznaczamy?

20. Wymień założenia, jakie przyjmujemy w przybliżonej analizie skręcanego pręta cienkościennego. Wyprowadź wzory dla obliczenia max w przekroju teowym

21. Przy jakim obciążeniu pręta mówimy o czystym skręcaniu ?.

22. Pręt o przekroju kołowym o długości l, utwierdzony na obu końcach skręcany jest momentem
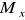
    przyłożonym w odległości a od lewej podpory. Oblicz reakcje.

23. Wypisz algorytm postępowania przy rozwiązaniu zagadnienia brzegowego czystego skręcania .podejściem kinematycznym

24. Napisz algorytm postępowania przy projektowaniu skręcanego pręta

25. Ile wynoszą ekstremalne wartości naprężeń stycznych w poszczególnych przedziałach pręta skręcanego (wspornik obciążony momentem skręcającym Ms na wolnym końcu), który wykonany jest z rury (Dw=0.8*Dz) rozciętej wzdłuż tworzącej na połowie długości pręta.

26. Obliczyć i narysować wykres kątów w poszczególnych przedziałach pręta skręcanego (wspornik obciążony momentem skręcającym Ms na wolnym końcu), który wykonany jest z rury (Dw=0.8*Dz) rozciętej wzdłuż tworzącej na połowie długości pręta.

27. Wspornik wykonany z rury (Dw=0.8*Dz) rozciętej wzdłuż tworzącej na połowie długości obciążony jest momentem skręcającym Ms w środku długości (w miejscu kończącym rozcięcie). Wyznaczyć wartość momentu skręcającego Mu, jaki należy przyłożyć na wolnym końcu pręta, aby kąt skręcenia tego przekroju wynosił 0.

Premia: Obliczyć maksymalne naprężenia styczne i narysować wykres kątów w poszczególnych przedziałach pręta.

28. Czy zagadnienie skręcania pręta o przekroju kołowym, do którego obu końców przyklejone są nieodkształcalne (sztywne) bloki można rozwiązywać w oparciu o poznane zagadnienie czystego rozciągania? Odpowiedź uzasadnić.

Premia: Czy odpowiedź na powyższe pytanie zależy od kształtu przekroju poprzecznego?

29. Podaj (na rysunku) geometryczną interpretację przemieszczeń punktów w płaszczyźnie przekroju poprzecznego pręta skręcanego (nie uwzględniać spaczenia, można posłużyć się przekrojem kołowym). Jakie założenie odgrywa w tym przypadku istotną rolę? Jaki byłby promień odkształconego przekroju kołowego w przypadku braku spełnienia warunków narzuconych przez to założenie i przyjęciu kąta obrotu danego przekroju = /2?.

30. Czy w pręcie skręcanym występują naprężenia normalne? Jeżeli tak, to, jaka jest ich największa wartość w pręcie o przekroju kołowym?. Odpowiedź uzasadnij.

---