STEREOMETRIA - zadania

1. Oblicz objętość graniastosłupa prawidłowego czworokątnego, którego przekątna podstawy ma długość
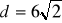
   cm, a pole powierzchni całkowitej P = 264 cm².

2. Pola trzech ścian prostopadłościanu są odpowiednio równe: P₁ = 35 cm², P₂ = 8 cm², P₃ = 112 cm². Oblicz objętość tego prostopadłościanu.

3. Oblicz objętość i pole powierzchni sześcianu, którego przekątna jest o 6 cm dłuższa od jego krawędzi.

4. W graniastosłupie prawidłowym trójkątnym o krawędzi podstawy a = 6 cm, przekątna ściany bocznej tworzy z drugą ścianą boczną kąt o mierze
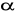
   = 30^o. Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa.

5. W graniastosłupie prawidłowym trójkątnym poprowadzono przez krawędź podstawy płaszczyznę przecinającą w środku przeciwległą krawędź boczną i tworzącą z podstawą kąt 45^o. Oblicz pole otrzymanego przekroju oraz pole powierzchni i objętość graniastosłupa, gdy krawędź podstawy ma długość
   .

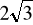
6. W graniastosłupie prawidłowym trójkątnym promień okręgu opisanego na podstawie ma długość 8 cm. Przekątna ściany bocznej jest nachylona do podstawy pod kątem 45^o. Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa.

7. W prawidłowym graniastosłupie trójkątnym pole powierzchni całkowitej jest dwa razy większe od sumy pól obu podstaw. Oblicz cosinus kąta nachylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej.

8. Oblicz objętość i pole powierzchni całkowitej graniastosłupa prawidłowego sześciokątnego o krawędzi podstawy długości a , którego najdłuższa przekątna nachylona jest do płaszczyzny podstawy pod kątem o mierze
   .

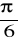
9. Podstawą graniastosłupa prostego jest romb o boku długości a = 5 i kącie ostrym
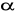
   = 60^o. Krótsza przekątna graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze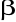
   = 45^o.

Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa.

10. Długości trzech krawędzi o wspólnym wierzchołku pewnego prostopadłościanu tworzą ciąg geometryczny. Objętość prostopadłościanu wynosi 1728 cm³. Oblicz pole powierzchni tego prostopadłościanu.

11. Dwa graniastosłupy proste mają wysokości o tej samej długości h. Podstawą jednego graniastosłupa jest kwadrat wpisany w okrąg o promieniu r. Podstawą drugiego graniastosłupa jest trójkąt równoboczny opisany na okręgu o tym samym promieniu r. Wyznacz stosunek pól powierzchni bocznych oraz stosunek objętości tych graniastosłupów.

12. Dany jest ostrosłup prawidłowy trójkątny o krawędzi podstawy a = 6 cm i kącie nachylenia krawędzi bocznej do podstawy
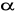
    = 60^o. Oblicz objętość i pole powierzchni ostrosłupa.

13. W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość k =
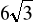
    , a kąt między wysokościami sąsiednich ścian bocznych wychodzących z wierzchołka ostrosłupa ma miarę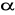
    = 60^o. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

14. W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość a = 4, a krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem o mierze
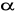
    = 45^o. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

15. Wysokość prawidłowego ostrosłupa czworokątnego ma długość h , a kąt ściany bocznej przy wierzchołku ostrosłupa ma miarę
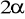
    . Oblicz pole powierzchni bocznej ostrosłupa.

16. W ostrosłupie prawidłowym trójkątnym promień okręgu opisanego na podstawie ma długość 2, a krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 60^o. Oblicz objętość ostrosłupa.

17. Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość a .Pole powierzchni bocznej tego ostrosłupa wynosi
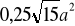
    . Oblicz miarę kąta nachylenia krawędzi bocznej do płaszczyzny podstawy.

18. Suma długości wszystkich krawędzi ostrosłupa prawidłowego trójkątnego jest dwa razy mniejsza niż suma długości wszystkich krawędzi pewnego sześcianu. Długość krawędzi podstawy ostrosłupa jest równa 12 a sinus kąta między krawędzią boczną i płaszczyzną podstawy tego ostrosłupa wynosi
    .

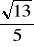
1. Oblicz objętość tego ostrosłupa oraz wyznacz cosinus kąta między krawędziami bocznymi ostrosłupa.

2. Oblicz stosunek pola powierzchni bocznej ostrosłupa do pola powierzchni całkowitej sześcianu.

19. Długość wysokości prawidłowego ostrosłupa czworokątnego wynosi
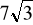
    , a krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 60^o.

1. Oblicz objętość i pole powierzchni całkowitej ostrosłupa.

2. Oblicz pole przekroju ostrosłupa płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do płaszczyzny podstawy pod kątem 30^o.

20. Długość krawędzi bocznej ostrosłupa prawidłowego trójkątnego wynosi
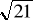
    . Ściana boczna ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze 60^o.

1. Oblicz objętość tego ostrosłupa oraz pole jego przekroju wyznaczonego przez wysokość i krawędź boczną ostrosłupa.

2. Oblicz odległość wierzchołka podstawy ostrosłupa od jego krawędzi bocznej.

21. W ostrosłupie prawidłowym czworokątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem o mierze 60^o.Odległość środka podstawy ostrosłupa od krawędzi bocznej wynosi
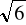
    dm. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

22. W ostrosłupie prawidłowym czworokątnym pole jednej ściany bocznej jest trzy razy mniejsze od pola podstawy. Oblicz objętość tego ostrosłupa przyjmując, że długość krawędzi podstawy wynosi 14 cm. Wyznacz sinus kąta między sąsiednimi krawędziami bocznymi tego ostrosłupa.

23. W prawidłowym ostrosłupie czworokątnym długość krawędzi bocznej jest równa długości krawędzi podstawy, a pole ściany bocznej jest równe 72
    .

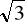
1. Oblicz objętość ostrosłupa oraz wyznacz odległość środka wysokości ostrosłupa od ściany bocznej.

2. Oblicz pole przekroju ostrosłupa płaszczyzną przechodzącą przez środki dwóch sąsiednich krawędzi podstawy i wierzchołek ostrosłupa.

24. W ostrosłupie prawidłowym czworokątnym kąt między wysokościami sąsiednich ścian bocznych wynosi 60^o.Pole powierzchni całkowitej tego ostrosłupa wynosi 16 ( 1 +
    ).

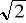
1. Wyznacz miarę kąta nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa.

2. Oblicz objętość tego ostrosłupa oraz odległość środka wysokości ostrosłupa od ściany bocznej.

25. Powierzchnia boczna walca po rozwinięciu jest kwadratem o przekątnej d =
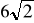
    cm. Oblicz pole powierzchni całkowitej i objętość walca.

26. Przekrój osiowy walca jest prostokątem o boku a = 8 i przekątnej d = 12. Oblicz objętość
    i pole powierzchni całkowitej tego walca.

27. Powierzchnia boczna stożka po rozwinięciu na płaszczyźnie jest półkolem o promieniu k = 6. Oblicz pole powierzchni całkowitej i objętość stożka oraz miarę kąta rozwarcia stożka.

28. Romb o kącie ostrym o mierze
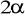
    i dłuższej przekątnej długości d obraca się dokoła krótszej przekątnej. Oblicz objętość i pole powierzchni całkowitej powstałej bryły.

29. W sześcianie wydrążono wnękę w postaci kuli o objętości 288
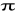
    . Wiedząc, że średnica kuli równa się krawędzi sześcianu, oblicz pole powierzchni powstałej bryły.

30. Suma długości trzech różnych krawędzi prostopadłościanu, które tworzą ciąg geometryczny rosnący wynosi 42. Jeżeli długość drugiej krawędzi zwiększymy o 3, a długość pozostałych krawędzi pozostawimy bez zmiany to długości krawędzi utworzą ciąg arytmetyczny. Oblicz stosunek pola powierzchni kuli opisanej na pierwszym prostopadłościanie do pola powierzchni kuli opisanej na drugim prostopadłościanie.

31. W graniastosłup prosty, którego podstawą jest trójkąt prostokątny wpisano kulę. Wysokość wyprowadzona z wierzchołka kąta prostego podstawy na przeciwprostokątną wynosi h = 8
    i tworzy z przyprostokątną kąt o mierze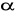
    = 30^o.Oblicz objętość graniastosłupa.

32. Objętość ostrosłupa prawidłowego czworokątnego o wysokości h = 6 cm wynosi 32 cm². Oblicz pole powierzchni całkowitej stożka, którego podstawą jest koło opisane na podstawie ostrosłupa, a wierzchołki tych brył pokrywają się.

33. Z ilu pomarańczy o średnicy 6 cm należy wycisnąć sok, aby napełnić 6 szklanek w kształcie walca wiedząc, że średnica dna szklanki ( wewnątrz ) ma 5 cm, a długość wysokości szklanki ( wewnątrz ) wynosi 8 cm. Zawartość soku stanowi 60% objętości pomarańczy.

34. Promień kuli opisanej na stożku ma długość R = 6, a kąt rozwarcia stożka ma miarę 120^o. Oblicz objętość i pole powierzchni całkowitej stożka.

35. Do wysokiego naczynia w kształcie walca o średnicy podstawy długości d = 16 cm zawierającego pewną ilość wody wrzucono kulę o promieniu długości r = 6 cm. Kula ta całkowicie zanurzyła się w wodzie. O ile centymetrów podniósł się poziom wody w tym naczyniu?

36. W sześcianie o krawędzi a, odcięto każde naroże i w ten sposób otrzymano 8 ostrosłupów prawidłowych trójkątnych o krawędzi bocznej
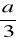
    . Oblicz pole powierzchni całkowitej, objętość i długość wszystkich krawędzi bryły, która powstała po odcięciu wszystkich naroży.

37. Jeżeli pewien trójkąt prostokątny obrócimy dokoła jednej z przyprostokątnych, to otrzymamy bryłę o objętości
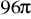
    cm³. Jeżeli ten sam trójkąt obrócimy dokoła jego przeciwprostokątnej, to otrzymamy bryłę, której objętość równa się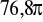
    cm³. Oblicz pole trójkąta prostokątnego.

38. Dany jest ostrosłup prawidłowy czworokątny, którego krawędź podstawy równa się krótszej przekątnej pewnego równoległoboku, a wysokość ostrosłupa dłuższej przekątnej równoległoboku o bokach długości a = 4 cm, b = 8 cm oraz kącie ostrym o mierze
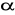
    = 30^o. Oblicz :

1. objętość i pole powierzchni tego ostrosłupa,

2. tangensy kątów nachylenia : ściany bocznej do podstawy i krawędzi bocznej do podstawy.

39. W prawidłowy ostrosłup czworokątny, którego długość krawędzi podstawy a = 36, a kąt
nachylenia ściany bocznej do płaszczyzny podstawy ma miarę
= 60^o wpisano sześcian tak,
że wierzchołki górnej podstawy sześcianu leżą na wysokościach ścian bocznych, a dolna
podstawa zawiera się w podstawie ostrosłupa. Oblicz stosunek pola powierzchni ostrosłupa do
pola powierzchni wpisanego sześcianu.

40. W kulę wpisano stożek, którego przekrojem osiowym jest trójkąt równoboczny o boku
długości a. Oblicz stosunek objętości kuli do objętości wpisanego stożka.

41. Na kuli o promieniu r opisano stożek, w którym tworząca nachylona jest do płaszczyzny
podstawy pod kątem o mierze
. Oblicz objętość i pole powierzchni całkowitej stożka.

42. Oblicz objętość kuli wpisanej w stożek o promieniu długości r = 7 dm i tworzącej długości
l = 25 dm.

59

---