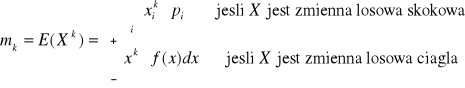
PARAMETRY ROZKŁADU ZMIENNEJ LOSOWEJ

Definicja

Momentem zwykłym rzędu k zmiennej losowej X nazywamy

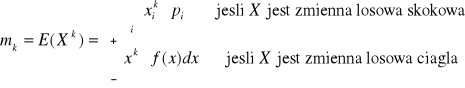
Definicja

Momentem centralnym rzędu k zmiennej losowej X nazywamy

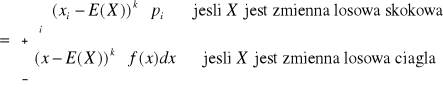
Własności E(X)

1° E(c)=c dla
,

2° E(aX+b)=aE(X)+b dla
,

3° E(X+Y)=E(X)+E(Y),

4° Jeśli zmienne losowe X i Y są niezależne, to E(X⋅Y)=E(X)⋅E(Y).

Własności D²(X)

1° D²(c)=0 dla
,

2° D²(aX+b)=a²D²(X) dla
,

3° D²(X+Y)=D²(X)+2E[(X-E(X))(Y-E(Y))]+D²(Y),

4° Jeśli zmienne losowe X i Y są niezależne, to D²(X+Y)=D²(X)+D²(Y).

WYBRANE ROZKŁADY ZMIENNEJ LOSOWEJ SKOKOWEJ

Rozkład dwupunktowy

Zmienna losowa X ma rozkład dwupunktowy, jeśli istnieją takie punkty x₁, x₂, że P(X = x₁) = p,

P(X = x₂) = 1 - p, gdzie 0 < p < 1.

Jeśli x₁= 1 i x₂ = 0, to taki rozkład nazywamy rozkładem zero-jedynkowym.

Dystrybuanta rozkładu zero-jedynkowego:

.

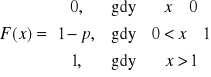
Parametry rozkładu zero-jedynkowego:

Rozkład dwumianowy (Bernoulliego)

Zmienną losową X o rozkładzie dwumianowym z parametrami (n, p) otrzymujemy w następującym schemacie doświadczeń, zwanym schematem Bernoulliego.

Schemat Bernoulliego

Dokonujemy n niezależnych doświadczeń losowych. W wyniku każdego doświadczenia może zajść zdarzenie A (sukces) z prawdopodobieństwem p i zdarzenie przeciwne A' (porażka) z prawdopodobieństwem 1 - p. Zmienna losowa X przyjmuje wartość równą liczbie sukcesów w n doświadczeniach.

Jeśli niezależne zmienne losowe X₁, X₂, . . . , X_n mają jednakowe rozkłady zero-jedynkowe z parametrem p, to zmienna losowa
ma rozkład dwumianowy z parametrami (n, p).

Funkcja prawdopodobieństwa w rozkładzie dwumianowym

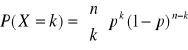
, gdzie k = 0, 1, ..., n.

Parametry rozkładu dwumianowego:

Rozkład Poissona

Zmienna losowa X ma rozkład Poissona z parametrem λ>0, jeśli funkcja prawdopodobieństwa ma postać

, gdzie k = 0, 1, ....

Parametry rozkładu Poissona:
.

Twierdzenie

Jeśli X₁, X₂, . . . , X_n, . . . jest ciągiem zmiennych losowych o rozkładach dwumianowych odpowiednio z parametrami (1, p₁), (2, p₂), ...., (n, p_n), .... oraz
(λ>0), to ciąg rozkładów dwumianowych jest zbieżny do rozkładu Poissona z parametrem λ.

Wniosek

Przybliżamy (dla dużego n i małego p)

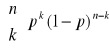
przyjmując
.

WYBRANE ROZKŁADY ZMIENNEJ LOSOWEJ CIĄGŁEJ

Rozkład jednostajny (równomierny, prostokątny)

Zmienna losowa X ma rozkład jednostajny na przedziale [a, b], jeśli jej funkcja gęstości ma postać

.

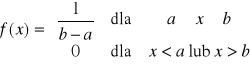
Dystrybuanta zmiennej losowej X o rozkładzie jednostajnym ma postać

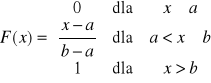
Parametry zmiennej losowej X o rozkładzie jednostajnym:
,

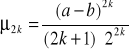
, dla k = 1, 2, ..., stąd
,

, dla k = 1, 2, ... (ponieważ funkcja gęstości jest symetryczna względem wartości oczekiwanej).

Rozkład normalny

Zmienna losowa X ma rozkład normalny z parametrami
, σ > 0, jeśli jej funkcja gęstości ma postać

,
.

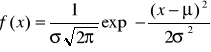
Dystrybuanta rozkładu normalnego ma postać

,
.

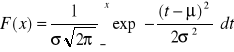
Parametry zmiennej losowej o rozkładzie normalnym:

,
,
.

Rozkład normalny nazywamy standaryzowanym (lub standardowym), jeśli μ = 0 i σ = 1.

Twierdzenie

Jeśli
.

Reguła trzech sigm

Prawdopodobieństwo, że wartość zmiennej losowej o rozkładzie normalnym będzie różnić się od wartości przeciętnej o mniej niż 1, 2, 3 odchylenia standardowe wynosi odpowiednio:

,
,
.

Twierdzenie

Niech {X_n} będzie ciągiem zmiennych losowych o rozkładach dwumianowych z parametrami (n, p), to ciąg dystrybuant zmiennych losowych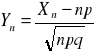
jest zbieżny do dystrybuanty rozkładu normalnego N(0,1).

Wniosek

Rozkład dwumianowy z parametrami (n, p) może być aproksymowany przez rozkład normalny
. Przybliżenie jest tym lepsze, im większe n oraz
.

Definicje i twierdzenia RACHUNEK PRAWDOPODOBIEŃSTWA ZSZ WZ UG

1

3