Zadania z matematyki dla studentów I - go roku studiów stacjonarnych

na kierunku ekonomia

Zestaw 8

1. Metodą eliminacji Gaussa rozwiąż układy równań:

a)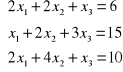
, b)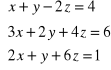
, c)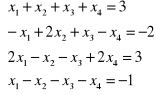
.

2. Metodą Gaussa-Jordana rozwiąż układy równań:

a)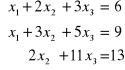
, b)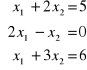
, c)
.

3. Znajdź przeciwobrazy podanych punktów w przekształceniach liniowych określonych macierzami:

a) A =
, y = (4, 2), b) B =
, y = (4, 2), c) C =
, y = (4, 2).

4. Wyznaczyć jądra przekształceń liniowych zadanych macierzami:

a)
, b)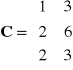
, c)
, d)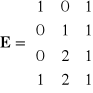
.

5. Wyznacz wszystkie rozwiązania bazowe układów równań:

a)
, b)
, c)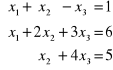
.

6. W skład posiłku mają wchodzić m.in. dwa składniki, zawierające witaminę A i B. Zawartość (w miligramach) każdej z witamin w jednym gramie każdego składnika podaje tabela:

	Składnik I	Składnik II	Wymagana ilość
Witamina A	0,03	0,06	50
Witamina B	0,1	0,03	70

Ile gramów każdego ze składników musi zawierać posiłek, jeśli wymagana ilość obu witamin określana jest liczbami podanymi w tabeli?

7. W tabeli opisano cechy trzech rodzajów papierów wartościowych:

	Akcje zwykłe	Akcje dające dywidendę	Obligacje
Spodziewany wzrost wartości w ciągu roku	12%	8%	5%
Spodziewany spadek wartości w ciągu roku	10%	8%	3%

Określić strategię zainwestowania 250 tys. zł. w te papiery wartościowe, jeżeli założony roczny wzrost wartości zainwestowanego kapitału ma wynieść 7%, a potencjalna strata określona jest na 5%.

---