1. Zasada pomiaru.

Celem ćwiczenia było wyznaczenie charakterystyki licznika Geigera - Millera , określenie napięcia progowego , obszary występowania „plateau” oraz wyznaczenie nachylenia „plateau”.

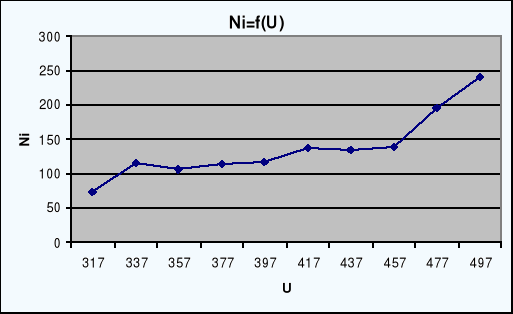
Długość „plateau” i odpowiadający mu przyrost zliczeń oraz liczbę zliczeń należy wyznaczyć z wykresu N = f(U).

Z tych danych wyliczamy nachylenie „plateau” wyrażające względny przyrost liczby zliczeń w obszarze prostoliniowym charakterystyki.

Nachylenie „plateau” liczymy ze wzoru:

Nachylenie „plateau” =

2. Schemat układu pomiarowego.

3. Tabela pomiarowa.

U	ni			Ni
[ V ]
317	70	76	73	44	7
337	123	108	115,5	70	8
357	120	92	106	64	8
377	124	104	114	68	8
397	123	110	116,5	70	8
417	139	136	137,5	82	9
437	144	125	134,5	80	9
457	139	139	139	83	9
477	188	202	195	117	11
497	218	263	240,5	144	12

4. Ocena dokładności pojedynczych pomiarów.

Błąd wartości N_i (liczba zliczeń) :

ΔU = ± 1% wartości mierzonej.

5. Przykładowe obliczenia wielkości złożonych.

ΔU₃ = 317 ⋅ 0,01 = 3,17 [V]

Nachylenie „plateau”: wartości odczytane z wykresu ΔU = 80 , ΔN = 15,5 , Np=75.

Nachylenie „plateau” =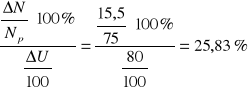

6. Wnioski.

Jak wynika z wykresu obszar występowania „plateau” zawiera się pomiędzy 377 [V]

a 457 [V]. W obszarze tym charakterystyka przebiega prawie liniowo a przyrost liczby zliczeń jest stosunkowo mały. Dopiero po przekroczeniu progu 457 [V] liczba zliczeń gwałtownie rośnie co oznacza , że obszar „plateau” się skończył.

---