Postulaty mech.kwantowej

1.'o funkcji falowej' - każdemu stanowi cząstki kwantowej przypisujemy funkcje falową Ψ(r,t)=Ψ(x,y,z,t). Jest to funkcja położenia i czasu przyjmująca wartości zespolone.

Np. Płaska fala materii

Ψ(r,t)=Aexp(i*(kr-ωt)

Ψ=Acos(kr-ωt)+iAsin(kr-ωt)

E=ħω , ω=E/ħ - czest. Kolowa. Fal

k=2π/λ , λ=h/p-dl.fali.de.Brogliea

λ=2π/k , k=p/ħ , p-pęd cząstki

2.'o probabilistycznej interpretacji f-kcji falowej'

Fcja: ρ(r,t)=ψ(r,t)∙ψ*(r,t)=|ψ(r,t)|^2

Gęstość prawdopodobieństwa znalezienie cząstki kwantowej w pkt ŕ=(x,y,z) w chwili `t'

1D: [ρ]=1/m ; [ψ]=1/m^1/2

Fale materii sa zatem falami prawdopodobieństwa:

P(Ω)=∫ρ(ŕ,t)*dv

3.Równanie Schrodingera:

M-masa cząstki , V(r)-potencjał cz. h(kr)=1.05E-34 [J*s]

Jeżeli En potencjalna V , nie zależy od czasu to mamy tzw. Stan stacjonarny, wtedy:

Ψ(r,t)=Φ(r)+φ(t)=Φ(r)exp(-iωt)=Φ(r)exp(-i(E/ħ)t)

Wstawmy taka postać do r.Schrodi

dψ/dt=i(E/ħ)Φ(r)exp(-i(E/ħ)t) ;

∆ψ=exp(-i(E/ħ)t)*∆Φ(r) ;

Postać r.Schro bez czasu:

4.'o stanach stacjonarnych'

F.Fal w postaci:

Ψ(r,t)=Φ(r)*exp(-i(E/ħ)t) , gdzie Φ(r) jest rozwiazanie r.Schr bez czasu

ĤΦ(r)=E*Φ(r) opisuje tzw. Stan stacjonarny cząstki w którym jej energia jest ustalona i = E

Zastosowania r.Schrodingera

1.elektron swobodny

V(r)=V(x,y,z)=0

r.Schrod bez czasu: ĤΦ(r)=E*Φ(r)

V=0 ; (-ħ^2/2m)∆Φ=EΦ; 1D:

∆Φ=∂2Φ/dx^2 ->

(- ħ^2/2M)* ∂2Φ/dx^2=EΦ /2M/ħ²

∂2Φ/dx^2 + 2ME/ ħ² * Φ(x)=0

2ME/ ħ² = k^2

∂2Φ/dx^2 + k^2*Φ(x)=0 rownanie oscylatora harmonicznego

Zasada nieoznaczoności Heisen:

Nie można jednocześnie zmierzyć z dowolna dokładnością współrzędnej cząstki i składowej pędu, która odpowiada tej współrzędnej.

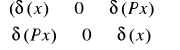
Ciało doskonale czarne

R(odbicie)=0 A(absorpcja)=1 , to takie ciało nazywamy doskonale czarnym.

Prawo Kirchoffa : stosunek zdolności emisyjnej do zdolności absorpcyjnej jest dla wszystkich powierzchni jednakową funkcją

, dla c.d.c E(υ,T)=ε(υ,T)

Rozkład Planc'a

∆E=h*υ

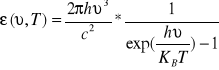
rozklad Plancka:

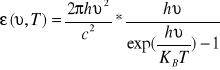
h=6.63E-34 J*s

Szczególne przypadki rozkładu Placka:

-fale krótkie hυ>>Kb*T

prawo Wienna - sluszne dla krótkich fal

-fale długie hυ<<Kb*T

prawo Rayleigha-Jensa - słuszne dla długich fal

Prawo Stefana Boltzmana:

Fotoefekt

-Liniowa zależność napięcia hamowania od częstotliwości światła

-Emax=eU0 nie zależy od natężenia światła

-brak opóźnienia czasowego miedzy oświetleniem fotokatody a pojawieniem się foto prądu

-rozchodzenie się EM należy rozpatrywać nie jako proces ciągły ale jako strumień zlokalizowanych w przestrzeni kwantów.

Takie kwanty = FOTONY

Zasada zachowania E w zjawisku fotoelektrycznym

Hυ=W+Ek , Ek=eU0 -> hυ=W+eU

Pęd fotonu:

Ef= hυ

Pf=(Ef/c)=( hυ/c)=h/λ

Zjawisko Comptona

Polega na tym że gdy wiązka promieniowania X o dł fali λ rozprasza się na fali metalowej to w promieniowaniu rozproszonym pojawia się prom. O dł. Fali λ' wieksze niż λ

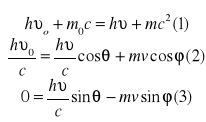
1.zasadza zachowania energii

2.zasada zachowania pędu kier X

3.zadafa zachowania pędu kier Y

↑z tw.Cos c2=a2+b2-2abcos(x)

Z(1): mc2=h(υ0-υ)+mc2 /^2 m2c4=h2(υ0-υ)^2+m₀2c4 (-4) m2c4(1-V2/c2)=M₀c4-2h2υυ₀(1-cosθ)+2M₀c2h(υ₀-υ)

2M₀c2h(υ₀-υ)=2h2υ₀*υ(1-cosθ)

c(υ₀-υ/ υ₀υ)=(h/m₀c)* υ₀υ(1-cosθ)

c(υ₀-υ/ υ₀υ)=c/υ - c/υ₀=(h/m₀c)( 1-cosθ)

λ=cT=c/υ, ostatecznie:

λ-λ₀=(h/m₀c)( 1-cosθ) wzor na przesunięcie Comptona

Dualizm falowo-cząstkowy

P=h/λ=2π/λ*h/2π

h/2π=ħ=1.05E-34Js

p= ħ*k_

E=hυ= ħ*ω

Model Bohra

Postulaty

1.Elektron porusza sie na orbicie kolowej wokol jadra

2.dozwolone sa tylko takie orbity 1,2,3 dla których orbitalny moment pedu elektronu jest wielokrotnascia stalej kreślonej planca

3.wypromieniowanie energi ma charakter kwantowy i nastepuje wtedy gdy elektron przeskakuje z jednej orbity na druga

Wzór Bohra:

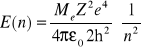
Serie widmowe wodoru:

Seria Lymana - nadfiolet

Seria Balmera - zakres widział

Seria Paschena - podczerwień

Seria Bracketa - podczerwien

Seria Pfunda - podczerwień

Seria Humpreysa - daleka podcze.

Zasada korespondencji Bohra:

Przewidywania fizyki kwantowej powinny odpowiadać przewidywaniom fizyki klasycznej w przypadku dużych liczb kwantowych.

Równanie oscylatora harmonicznego

Równanie falowe:

Równanie fali EM

Zasada Huygensa

Każdy punkt ośrodka do którego dociera fala staje się źródłem nowej fali kulistej

Zasada Fermata

Fala porusza się miedzy dwoma punktami ośrodka po takiej drodze,na której pokonanie zużywa najmniej czasu

Warunek Wulfa-Bragów

2dsinθ=nλ

---