Marcelina Arabucka Konrad Dróżka Rafał Witkowski

110332 110368 110489

Wydział: Fizyka Techniczna, Informatyka i Matematyka Stosowana

Kierunek: Informatyka

Semestr: V

Rok Akademicki: 2003/2004

Laboratorium Fizyki

Ćwiczenie nr 523

Dyfrakcja elektronów na polikrystalicznej warstwie grafitu

Ocena:

Dyfrakcja elektronów na polikrystalicznej warstwie grafitu.

1.Opis metody pomiaru.

Postulat de Broglie'a głosi, że z cząstką materialną o pędzie p można związać falę o długości

(1)

gdzie: h - stała Plancka.

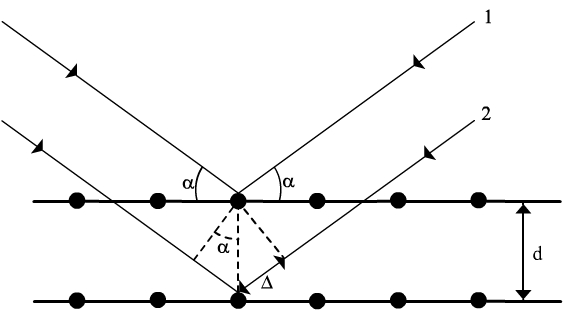
Wiązka rozpędzonych cząstek - w tym przypadku elektronów - powinna ulegać załamaniu, dyfrakcji i interferencji w sposób analogiczny jak fale. Tak jak fale wiązka elektronów padając na odpowiednią siatkę dyfrakcyjną będzie tworzyć maksima i minima interferencyjne. W naszym przypadku rolę siatki dyfrakcyjnej pełni sieć krystaliczna. Płaska fala elektronów o długości λ padając na kryształ ulega odbiciu od jego płaszczyzn sieciowych (rys.1). Jeżeli różnica dróg 2Δ przez dwa odbite promienie wynosi nλ (gdzie n = 1,2,3...) to promienie te dotrą do ekranu w zgodnych fazach i dadzą maksimum interferencyjne. Z rysunku wynika, że
a zatem warunkiem na maksimum interferencyjne jest spełnienie równania:

(2)

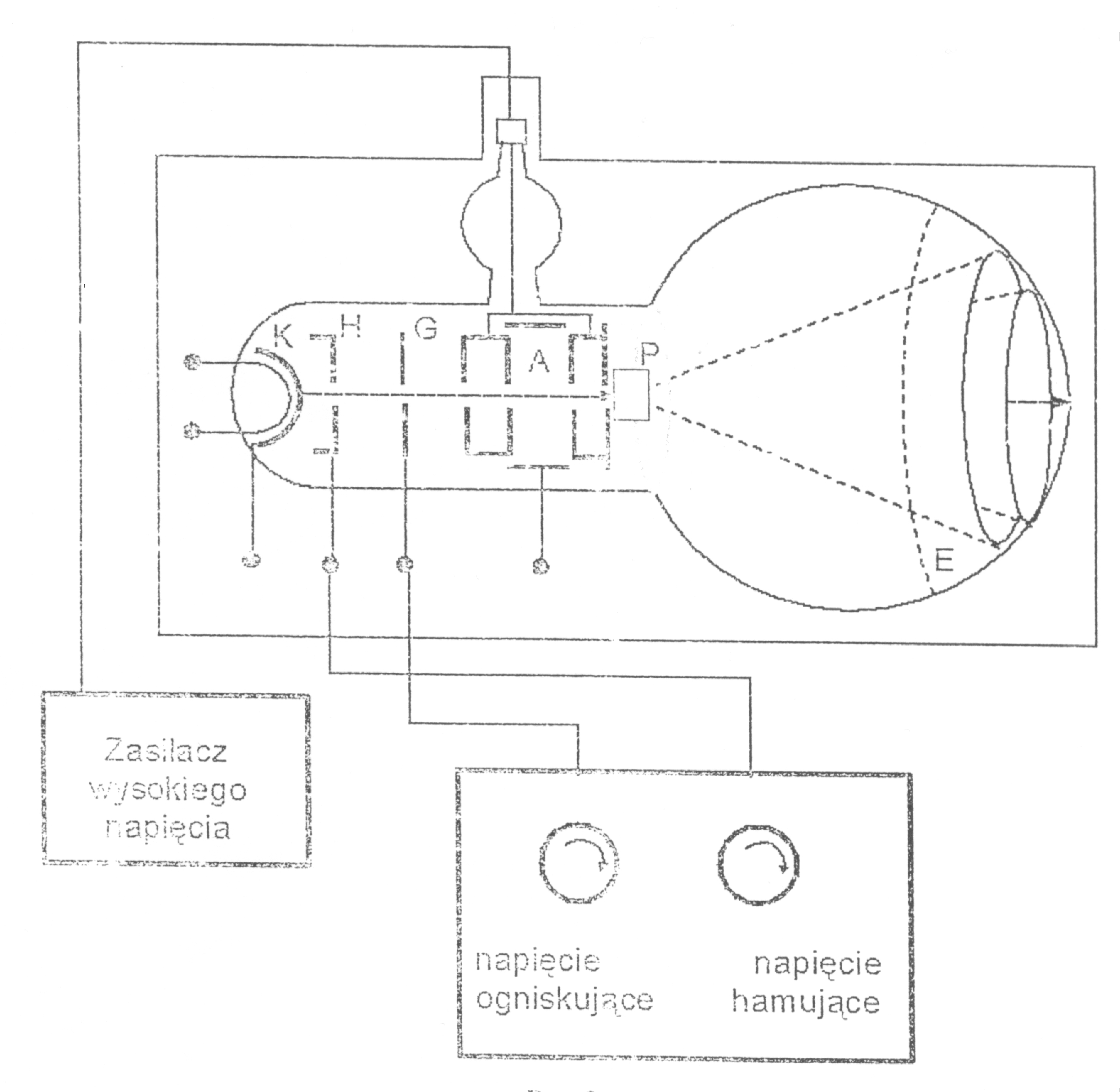
Do doświadczenia używamy następującego zestawu. Jego zasadniczą częścią jest szklana lampa próżniowa, w której znajduje się katoda K będąca źródłem elektronów, cylinder Wenhelta H służący do regulacji natężenia wiązki elektronów, elektrody ogniskujące wiązkę G, anoda A, próbka grafitu polikrystalicznego P, na której następuje ugięcie elektronów oraz ekran pokryty luminoforem E, na którym widoczny jest ślad wiązki ugiętej.

Wiązka elektronów wybiegająca z katody K zostaje przyspieszona w polu elektrycznym wytworzonym pomiędzy katodą a anodą. Elektrony padając na warstwę polikrystalicznego grafitu ulegają odbiciu od płaszczyzn sieciowych a następnie padają na ekran luminescencyjny powodując jego świecenie. Część wiązki padającej, która zostaje odbita od tych płaszczyzn tworzy wiązkę odbitą w kształcie stożka. Obrazem tego stożka na ekranie lampy jest okrąg.

Jeżeli pomiędzy katodę a anodę lampy przyłożone zostanie napięcie U_A to energia kinetyczna elektronów docierających do anody wynosić będzie:

(3)

gdzie: e - ładunek elektronu.

Energia kinetyczna z drugiej strony przedstawia się następująco:

(4)

gdzie: p - pęd elektronu; m- masa spoczynkowa elektronu.

Z obu wzorów można wyznaczyć pęd elektronu docierającego do warstwy grafitu:

(5)

Zgodnie ze wzorem (1) odpowiada mu fala o długości:

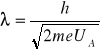
(6)

Aby fala o tej długości dała maksimum interferencyjne po odbiciu się od dwóch płaszczyzn sieciowych odległych o d muszą być spełnione warunki (2) i (6) co sprowadza się do równania:

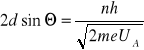
(7)

Mierząc kąt Θ i znając rząd interferencji n można obliczyć odległości płaszczyzn sieciowych, od których nastąpiło odbicie. Ponieważ jasność obrazu interferencyjnego szybko maleje wraz ze wzrostem rzędu interferencji, co, w niezaciemnionym pomieszczeniu praktycznie uniemożliwia zobaczenie okręgów odpowiadających n>1 należy przyjąć, że obserwowane okręgi odpowiadają rzędowi n = 1.

Z równania (7) wynika, że zależność sinΘ od
jest funkcją liniową a współczynnik nachylenia tej prostej wynosi

(8)

Za pomocą skali kątowej umieszczonej na obudowie lampy można zmierzyć kąt α odpowiadający szerokości kątowej otrzymanych na ekranie okręgów. Ponieważ oś skali kątowej przechodzi przez środek lampy to pomiędzy kątami α i Θ istnieje zależność:

(9)

2.Tabele z wartościami wielkości mierzonych i wyliczonych.

Zmierzone wartości kątów α dla odpowiadających im napięć U_A: (oryginalną kartkę z wynikami dołączamy do sprawozdania)

L.p.	UA [kV]	αa1 [°]	αb1 [°]	αa2 [°]	αb2 [°]
1	4,0	11	11	18	18
2	4,5	10	10	19	19
3	5,0	10	10	17	17
4	5,5	9	9,5	16	17
5	6,0	8,5	10	15,5	16,5
6	6,5	8	9	15	16
7	7,0	8	8,5	14	15
8	7,5	7,5	8	14	15
9	8,0	7	8	13,5	15
10	8,5	7	8	13	14,5
11	9,0	7	8	13	14

Wyznaczone wartości dla:
, kątów Θ oraz sinusów tych kątów:

L.p.	[V^-1/2]	ၑေaၛႰၝ	ၑေbၛႰၝ		sin	ၑဲb ၛႰၝ	ၑဲb ၛႰၝ		sin
1	0,5	2,75	2,75	2,75	0,04798	4,5	4,5	4,5	0,07846
2	0,4714	2,5	2,5	2,5	0,04362	4,75	4,75	4,75	0,08281
3	0,44721	2,5	2,5	2,5	0,04362	4,25	4,25	4,25	0,07411
4	0,4264	2,25	2,375	2,3125	0,04035	4	4,25	4,125	0,07193
5	0,40825	2,125	2,5	2,3125	0,04035	3,875	4,125	4	0,06976
6	0,39223	2	2,25	2,125	0,03708	3,75	4	3,875	0,06758
7	0,37796	2	2,125	2,0625	0,03599	3,5	3,75	3,625	0,06323
8	0,36515	1,875	2	1,9375	0,03381	3,5	3,75	3,625	0,06323
9	0,35355	1,75	2	1,875	0,03272	3,375	3,75	3,5625	0,06214
10	0,343	1,75	2	1,875	0,03272	3,25	3,625	3,4375	0,05996
11	0,33333	1,75	2	1,875	0,03272	3,25	3,5	3,375	0,05887

3. Wykresy.

Współczynniki nachylenia prostej oraz ich błędy liczymy korzystając z metody najmniejszych kwadratów. Prosta ma wzór:

Korzystamy z następujących wzorów:

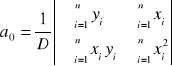
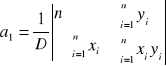
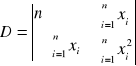
Błąd współczynnika kierunkowego a₁ wyliczamy ze wzoru:

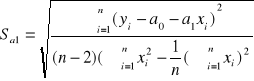
Wykres zależności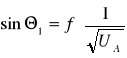
.

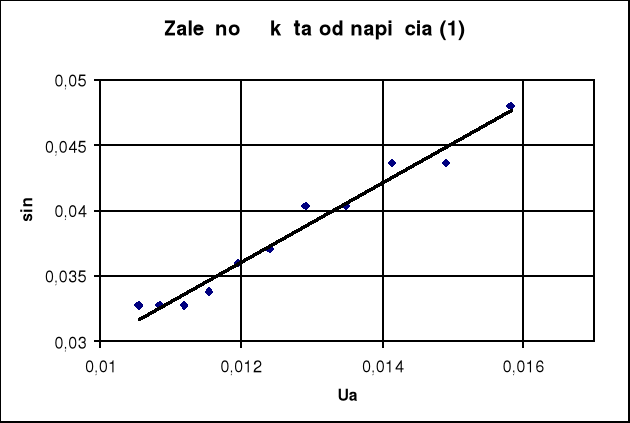
Współczynnik nachylenia prostej oraz błąd bezwzględny wynoszą odpowiednio:

. Wykres zależności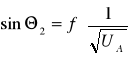
.

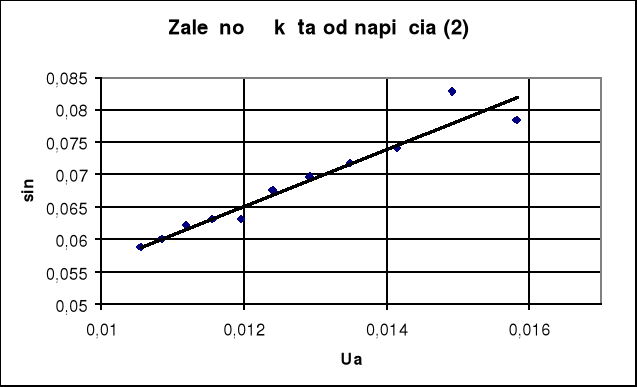
Współczynnik nachylenia prostej z powyższego rysunku, obliczony metodą najmniejszych kwadratów, oraz błąd bezwzględny dla współczynnika nachylenia wynoszą odpowiednio:

4.Wyznaczenie długości między płaszczyznowych.

Wyniki otrzymanych ze wzoru (8) długości między płaszczyznowych wynoszą:

Rachunek jednostek:

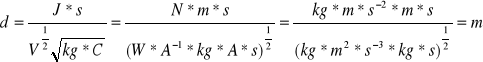
Błędy dla powyższych wartości, policzone metodą różniczki zupełnej, to:

5.Wynik końcowy i wnioski.

W ćwiczeniu wyznaczyliśmy dwie wartości odległości między płaszczyznowych dla grafitu: d₁ = 203,1 pm oraz d₂ = 140,7 pm. Porównując te wartości z wielkościami umieszczonymi na rysunku w instrukcji gdzie podane są wartości d₁ = 142 pm, d₂ = 123 pm uzyskujemy rozbieżności. Głównym czynnikiem powodującym to jest na pewno niepoprawny odczyt kątów, gdyż okręgi nie miały ostrych krawędzi. Regulacja napięcia ogniskującego nie zawsze była skuteczna, bowiem przy mały napięciu okręgi ulegały zanikowi.

Błąd względny jest dosyć duży w pierwszym przypadku ok.40% natomiast w drugim wynosi on ok.14%.

---