Marcelina Arabucka Konrad Dróżka Rafał Witkowski
110332 110368 110489
Wydział: Fizyka Techniczna, Informatyka i Matematyka Stosowana
Kierunek: Informatyka
Semestr: V
Rok Akademicki: 2003/2004
Laboratorium Fizyki
Ćwiczenie nr 417
Dyfrakcja i interferencja światła
Ocena:
Dyfrakcja i interferencja światła.
1.Opis metody pomiaru.
Z falowej natury światła wynika możliwość dyfrakcji i interferencji. Zgodnie z zasadą Huyghensa każdy punkt, do którego dochodzi fala, staje się źródłem nowej fali kulistej. Zasada ta tłumaczy zjawisko dyfrakcji, czyli ugięcia światła przy przechodzeniu przez otwory oraz interferencji - nakładania się fal.
W doświadczeniu badaliśmy natężenie prądu w fotodiodzie, na którą padała wiązka lasera po przejściu przez siatkę dyfrakcyjną oraz przez układ dwóch szczelin.
Pomiar rozkładu natężenia w obrazie dyfrakcyjnym jest realizowany za pomocą specjalnego układu doświadczalnego, w którego skład wchodzi:
laser He-Ne o długości fali λ=632,8 nm
układ zwierciadeł
ekran z umieszczonym w środku detektorem (fototranzystor) w osłonie o niewielkiej aparaturze kątowej
ramię napędzane mechanizmem śrubowym służące do ustawiania kąta, pod którym wiązka światła uległa dyfrakcji
Układ pomiarowy pozwala mierzyć względne natężenie światła w różnych punktach obrazu dyfrakcyjnego. Zawierający przesłonę stolik można obracać tak, by na fototranzystor padało światło pod różnym kątem biegnące z układu laser-przesłona. Dzięki temu można wyznaczyć natężenie światła w funkcji kąta θ, pod jakim badany promień opuszcza przesłonę. Tak uzyskane wyniki należy skonfrontować z teoretycznie wyznaczonymi zależnościami:
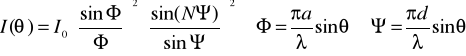
, (1)
gdzie:
![]()
- natężenie oświetlenia w punkcie ekranu położonym na osi układu źródło światła - układ szczelin - ekran.
![]()
- kąt, pod którym obserwujemy układ szczelin z określonego miejsca ekranu
a - szerokość szczeliny
d - odległość między osiami szczelin
λ - długość fali padającej na układ szczelin
N - ilość szczelin
W doświadczeniu mieliśmy do dyspozycji dwa elementy dyfrakcyjne:
siatka dyfrakcyjna (150 dpi)
podwójną szczelinę
2.Tabele z wynikami oraz wykresy.
Tabele z wielkościami mierzonymi załączamy do sprawozdania.
Przedstawione poniżej wykresy przedstawiają prąd fototranzystora w funkcji kąta obrotu, został on obliczony na podstawie ilości impulsów z czujnika umieszczonego na mechanizmie obracającym układ (skok 0.2 mrad). Pokazujemy dla każdego przypadku dwa wykresy: jeden obrazuje uzyskane przez nas dane, natomiast drugi przedstawia dane teoretyczne wyliczone ze wzoru (1). Wartości dla wyników obliczonych są normalizowane dla uzyskania możliwie wysokiego współczynnika korelacji.
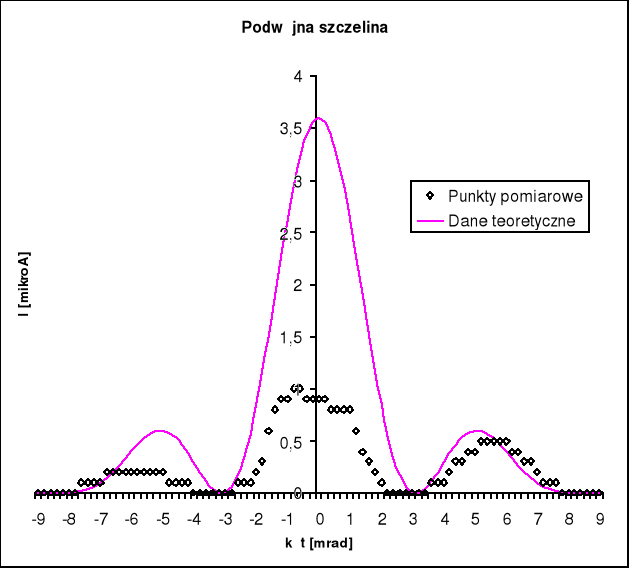
Dla podwójnej szczeliny otrzymaliśmy takie współczynniki:
d = 1.0*10-4 m
a = 0,9*10-4 m
R = 0,69 (współczynnik korelacji)
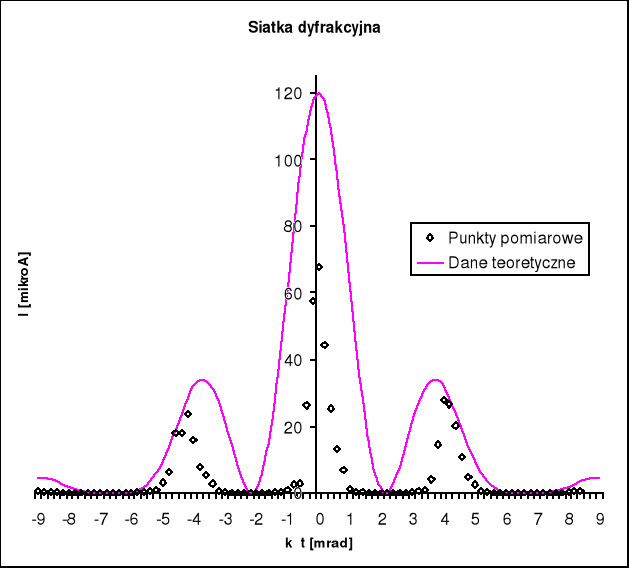
Dla siatki dyfrakcyjnej otrzymaliśmy takie współczynniki:
d = 1.0*10-4 m
a = 0,7*10-4 m
R = 0,89 (współczynnik korelacji)
Wartość współczynnika korelacji wyznaczaliśmy korzystając z wbudowanej w program MS EXCEL funkcji.
4.Wnioski i dyskusja czynników powodujących błędy.
Doświadczenie to dało nam tylko wyniki poglądowe, gdyż, aby rezultat był dokładny należałoby spełnić wiele elementów wpływających na dokładność oraz na zabezpieczenie bardzo delikatnej aparatury, oto kilka przyczyn czynników negatywnie wpływających na wyniki:
doświadczenie to powinno być przeprowadzane w pomieszczenie zapewniającym minimalny wpływ oświetlenia zewnętrznego na obraz dyfrakcji, nasza aparatura była wystawiona na działanie światła słonecznego, światła sztucznego pochodzącego z oświetlenia sali oraz modyfikacje tych źródeł poprzez ruch studentów wokół.
nasz mikroamperomierz nie zawsze wskazywał jednoznacznie pomiar prądu, często bywało tak, że musieliśmy wybrać wartość, wokół której oscylował.
pewne zużycie aparatury (zabrudzenia na zestawie zwierciadeł itp.) powodowały, że obraz, który obserwowaliśmy był częściowo rozmyty.
luzy w układzie pozycjonującym stolik powodowały, że można było poruszyć cały układ.
Jednakże pomimo wielu czynników powodujących błędy, doświadczenie w ogólnym stopniu potwierdziło założenia teoretyczne. Współczynniki korelacji wyników uzyskanych z wyliczonymi są wystarczające (siatka - R = 0,89 szczeliny - R = 0,69)
Wyszukiwarka
Podobne podstrony:
Doświadczenie 523, MIBM WIP PW, fizyka 2, laborki fiza(2), 37-Dyfrakcja elektronów i światła na siec
Ćw 523, MIBM WIP PW, fizyka 2, laborki fiza(2), 37-Dyfrakcja elektronów i światła na sieci krystalic
30, MIBM WIP PW, fizyka 2, laborki fiza(2), 37-Dyfrakcja elektronów i światła na sieci krystalicznej
523 zabol, MIBM WIP PW, fizyka 2, laborki fiza(2), 37-Dyfrakcja elektronów i światła na sieci krysta
Odpowiedzi do laborki 523, MIBM WIP PW, fizyka 2, laborki fiza(2), 37-Dyfrakcja elektronów i światła
Doświadczenie 412, MIBM WIP PW, fizyka 2, laborki fiza(2), 25-Interferencja światła, pierścienie New
C 4, MIBM WIP PW, fizyka 2, laborki fiza(2), 31-Ruch elektronu w polu magnetycznym i elektrycznym. W
C -4 -, MIBM WIP PW, fizyka 2, laborki fiza(2), 31-Ruch elektronu w polu magnetycznym i elektrycznym
A-2p, MIBM WIP PW, fizyka 2, laborki fiza(2), 31-Ruch elektronu w polu magnetycznym i elektrycznym.
C 4 , MIBM WIP PW, fizyka 2, laborki fiza(2), 31-Ruch elektronu w polu magnetycznym i elektrycznym.
Cwiczenie 31, MIBM WIP PW, fizyka 2, laborki fiza(2), 31-Ruch elektronu w polu magnetycznym i elektr
Sprawozdanie nr 31, MIBM WIP PW, fizyka 2, laborki fiza(2), 31-Ruch elektronu w polu magnetycznym i
ADAAM22, MIBM WIP PW, fizyka 2, laborki fiza(2), 31-Ruch elektronu w polu magnetycznym i elektryczny
SPR B 6, MIBM WIP PW, fizyka 2, laborki fiza(2), 31-Ruch elektronu w polu magnetycznym i elektryczny
A-22WLAD, MIBM WIP PW, fizyka 2, laborki fiza(2), 31-Ruch elektronu w polu magnetycznym i elektryczn
więcej podobnych podstron