POLITECHNIKA ŚLĄSKA W GLIWICACH

Wydział: MECHANICZNY - TECHNOLOGICZNY

Kierunek: AUTOMATYKA I ROBOTYKA

Grupa: V

sekcja: 2

LABORATORIUM Z MECHANIKI OGÓLNEJ

Macierzowa analiza sił w prętach kratownicy płaskiej

Opracował:

MARIUSZ FORNAL

CZĘŚĆ TEORETYCZNA

Celem ćwiczenia jest zapoznanie się z zastosowaniem rachunku macierzowego do określania sił w prętach płaskiej kratownicy statycznie wyznaczalnej.

Kratownice statycznie wyznaczalną nazywamy tak wtedy gdy liczba niewiadomych sił w prętach oraz reakcji podporowych jest równa liczbie równań równowagi. Rozważania do kratownic płaskich spełniających założenia technicznej kratownic, tzn. odpowiednio podpartych (statycznie zewnętrznie wyznaczalnych) geometrycznie niezmiennych zbudowanych z prętów przegubowych i obciążonych w węzłach. W takim przypadku siły w prętach tworzy w każdym z węzłów kratownicy zbieżny układ sił. Dla kratownicy posiadającej m węzłów oraz n prętów możemy napisać 2m równań odpowiadających rzutom sił na osie układu współrzędnych:

a₁₁xS₁ +a_12xS₂+ a_13xS₃ +... a_nxS_n + P_ix = 0

a_11yS₁ +a_12yS₂+ a_13yS₃ + ... a_nyS_n + P_iy = 0

I = 1 …, m, j = 1 …, n,

a_i1xS₁ +a_i2xS₂+ a_i3xS₃ + ... a_inxS_n + P_ix = 0

a_i1yS₁ +a_i2yS₂+ a_i3yS₃ + ... a_inxS_n + P_iy = 0

gdzie:

S - siła wewnętrzna w pręcie o numerze j = 1 …, n,

a_ijx, a_ijy - współczynniki w równaniu równowagi dla węzła i = 0 … m odpowiednio z rzutowanym na osie x i y układu współrzędnych stojące przy sile o numerze j

P_ix, P_iy - rzuty sił zewnętrznych (uwzględniając reakcje więzów) na osie x i y układu współrzędnych przyłożonych w węźle i.

Współczynniki a_ijx, a_ijy - mogą być równe zero lub być różne od zera w zależności od tego, czy dany pręt występuje w rozpatrywanym węźle, czy też nie występuje. Układ równań równowagi możemy zapisać zatem w postaci macierzowej:

P = - A⋅S

gdzie:

P - macierz kolumnowa składowych sił zewnętrznych przyłożonych w węzłach zawierające niewiadome podporowe

A - macierz współczynników równań równowagi węzłów

S - macierz kolumnowa sił wewnętrznych

Istota macierzowej metody wyznaczania sił w prętach kratownicy polega więc na automatycznym generowaniu równań równowagi wszystkich węzłów kratownic I zapisaniu ich w postaci macierzowej. Równania te umożliwiają wyznaczanie sił we wszystkich n prętach oraz wyznaczanie 3 niewiadomych reakcji podporowych. Kluczem do tej metody jest macierz A, której struktura zależy od postaci konstrukcyjnej analizowanej kratownicy.

Budowa macierzy połączeń

Macierz połączeń zawiera konfigurację kratownicy, tzn. Zapisana w niej informacja o połączeniach prętów w poszczególnych węzłach. Obliczenia rozpoczynamy od ponumerowania w dowolnej kolejności węzłów I prętów w kratownicy. Przyjmujemy, że początkiem pręta jest węzeł o niższym numerze. Następnie budujemy macierz połączeń:

K =
i = 1 …, m j = 1 …, n

gdzie:

n - liczba węzłów

m - liczby prętów

i - numer węzła

j - numer pręta

Wiersze macierzy A odpowiadają węzłom, a kolumny prętom. W każdej kolumnie znajdują się tylko dwa niezerowe elementy:

„1” - w wierszu o numerze równym numerowi węzła, który jest początkiem pręta

„1” - wierszu odpowiadającym końcowi pręta

Budowa macierzy współrzędnych węzłów

Odbieramy dowolny prostokąt układ współrzędnych. Dla uproszczenia zapisu osie układu oznaczamy jako 1 i 2 w miejsce x i y. Macierz współrzędnych węzłów ma następującą postać:

X =
; i = 1..., m; j = 1..., n

Wiersze macierzy odpowiadają poszczególnym węzłom kratownicy, natomiast kolumny współrzędnym węzłów względem osi 1 i 2.

Budowa macierz cosinusów kierunkowych

W macierzy tej zapisane są cosinusy kierunkowe poszczególnych prętów kratownicy, a co za tym idzie, poszczególnych sił wewnętrznych. Zbudowanie tej macierzy wymaga określenia składowych długości prętów w przyjętym układzie współrzędnych oraz wyznaczenie ich całkowitej długości. Na tej podstawie możemy określić dopiero cosinusy nachylenia poszczególnych prętów kratownicy do osi układu współrzędnych. Macierz składowych długości prętów:

D
i = 1, 2 j = 1, 2 ... m

Obliczamy z równania:

D = - K^TX

Długości prętów są równe:

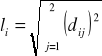
a, ich cosinusy kierunkowe:

c_ij = cosα_ij =

Macierz cosinusów kierunkowych C ma następującą postać:

Wiersze macierzy odpowiadają odpowiednim prętom kratownicy, natomiast kolumny cosinusów kątów nachylenia prętów do osi 1 i 2 układu współrzędnych.

Budowa macierzy sił zewnętrznych

Zakładamy, że w węzłach kratownicy przyłożone są siły zewnętrzne, których składowe są elementami macierzy F.

Między macierzami sił zewnętrznych P i wewnętrznych S zachodzi związek a równowagi węzłów:

P = -A⋅S

Budowa macierzy współczynników równań równowagi węzłów

Macierz A powstaje z macierzy K przez podstawienie w miejsce elementów:

„1” - odpowiednich wierszy macierzy cosinusów kierunkowych z macierzy C, odpowiadających poszczególnym prętom kratownicy

„-1” - jw., ale ze znakiem przeciwnym

„0” - dwuelementowego wektora zerowego

Wyznaczanie sił wewnętrznych wymaga wyeliminowania z macierzy A wierszy, a z macierzy kolumnowej P elementów odpowiadających warunkom podparcia. Po rozwiązaniu takiego uproszczonego układu równań wyznaczamy siły wewnętrzne w prętach kratownicy. Wartość dodania siły oznacza, że pręt jest rozciągany, a ujemna, że ściskany. Znając wartość tych sił i korzystając z odrzuconych równań zawierających składowe reakcji możemy wyznaczyć reakcje w podporach.

CZĘŚĆ PRAKTYCZNA

Ćwiczenie rozpoczynamy od narysowania schematu kratownicy płaskiej, ustalenia numeracji węzłów i prętów, miejsc podparcia przez podporę stałą i przesuwną.

Warunek statycznej wyznaczalności kratownicy:

p = 2w - 3

11 = 11

Kratownicy jest statycznie wyznaczalna

Budowa macierzy połączeń:

K=

Budowa macierzy współrzędnych węzłów:

X =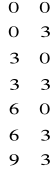

Po wprowadzeniu do komputera wszystkich danych otrzymaliśmy następujące wyniki:

D =

Wektor długości prętów:

L = [3; 3; 3; 3; 3; 3; 3; 3;

4.2426; 4.2426; 4.2426]

Macierz cosinusów w prętach:

C =

Siły występujące w prętach:

s₁ = 0

s₂ = -3.333

s₃ = -3.333

s₄ = 0

s₅ = 6.667

s₆ = -6.667

s₇ = 3.333

s₈ = 3.333

s₉ = 4.714

s₁₀ = -9.428

s₁₁ = 4.714

Jak zostało wspomniane wcześniej ujemne wartości sił oznaczają, że dany pręt jest ściskany.

Reakcje w podporach - podpora stała:

R_ax = 0.00

R_ay = 3.333

R_A = 3.333

• podpora przesuwna:

R_B = -6.667

Kąt pomiędzy R_B i osią αOY = 0

WNIOSKI:

Kratownice znajdują wielkie zastosowanie w wielu konstrukcjach ze względu na swą lekkość i prostotę wykonania.

Skorzystanie z programu komputerowego umożliwia bardzo dokładne obliczenie takich wartości jak:

- sił działający w prętach kratownicy

- sił w podporach, z dokładnym odwzorowaniem graficznym

- długości prętów

2

---