UKŁADY RÓWNAŃ I NIERÓWNOŚCI LINIOWYCH

Postać ogólna:

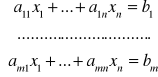
Postać macierzowa:

AX=B

Jednorodny układ równań, gdy b₁=b₂=...=b_m=0

Niejednorodny układ równań, gdy co najmniej jedna z liczb b₁,...,b_m jest różna od zera i wówczas:

.

Rozwiązanie u.r. - taki układ liczb x₁,...,x_n, które spełniają każde z równań układu.

• Układ sprzeczny

• Układ równań niezależnych

• Układ równań zależnych

Układ Cramera równań niejednorodnych

1. m=n

2. rząd r(A)=n

I sposób rozwiązania

Układ Cramera ma dokładnie jedno rozwiązanie postaci:

W - wyznacznik macierzy A,

W_k - wyznacznik utworzony z W przez zastąpienie k-tej kolumny , kolumną wyrazów b₁,...,b_m.

II sposób rozwiązania

AX=B

A^-1⋅AX=A^-1⋅B

IX=A^-1⋅B

X=A^-1⋅B

Przykład 1

Rozwiązać układ równań:

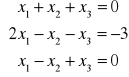
1. m=n=3

2. r(A)=3

Rozwiązanie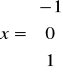

Twierdzenie Kroneckera-Capelliego

Na to aby układ równań nie był sprzeczny, potrzeba i wystarcza, aby r(A)=r(U), gdzie:

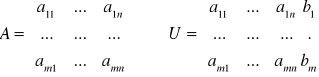
Przykład 2

Rozwiązać układ równań:

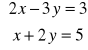
Operacje elementarne

Definicja

Dwa niesprzeczne układy równań liniowych są równoważne, wtedy i tylko wtedy gdy dowolne rozwiązanie jednego z nich jest również rozwiązaniem układu drugiego.

Definicja

Operacją elementarną na układzie jest każde przekształcenie układu równań AX=B w układ równoważny CX=D.

Układ CX=D → postać bazowa układu AX=B

Rodzaje operacji elementarnych:

1. Mnożenie dowolnego równania układu przez liczbę.

2. Dodawanie do dowolnego równania układu liniowej kombinacji innych równań układu.

3. Przestawienie dwóch dowolnych równań układu.

4. Pominięcie dowolnego, tożsamościowego równania układu.

UKŁADY NIERÓWNOŚCI LINIOWYCH

Postać ogólna:

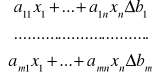
Symbol Δ oznacza: <, ≤, >, ≥.

Postać macierzowa:

AX Δ B

Rozwiązaniem układu równań nazywamy układ n liczb spełniających wszystkie nierówności układu.

Układ nierówności jest sprzeczny, jeżeli nie ma rozwiązania.

Przykład 5

Znaleźć zbiór rozwiązań nierówności:

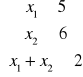
Przykład 6

Na fermie hodowlanej bydło karmi się świeżym sianem i paszą. Kilogram siana zawiera 40 g białka, 2 g wapna, 2 g fosforu i kosztuje 1,2 zł. Kilogram paszy zawiera 10 g białka, 3 g wapna, 1 g fosforu i kosztuje 0,8 zł. Określ dietę bydła w taki sposób, aby spożywało dziennie nie mniej niż 1 kg białka, 120 g wapna, 80 g fosforu i aby dieta była najtańsza z możliwych.

Przykład 7

Przedsiębiorstwo przemysłu metalowego produkuje dwa wyroby A i B, do których produkcji zużywa stal (kg) i pracę ludzką (roboczogodziny). Normy zużycia tych czynników produkcji oraz ich zasoby znajdujące się w posiadaniu przedsiębiorstwa przedstawia tablica:

Czynnik produkcji	Normy zużycia		Zasób czynnika
		A		B
Stal	40	16	640
Praca	10	2	140

Zysk osiągnięty z jednostki wyrobu A wynosi 9 jednostek pieniężnych, a zysk z wyrobu B 3 jednostki pieniężne. Określ optymalny plan produkcji przedsiębiorstwa, przyjmując jako kryterium optymalności zysk oraz ustal zużycie czynników produkcji i wykorzystanie zasobów.

Układy równań ...

1

2

---