Wykład 7 4.04.01.
Kinematyka płynów
Kinematyka płynów :
geometryczny opisem ruchu płynów, bez wnikania w pole sił powodujących przepływ,
wykorzystanie zasady analizy matematycznej, co wymaga przyjęcia założenia że płyn jest ośrodkiem ciągłym pod względem masy i odkształceń postaciowych jak i objętościowych,
masa i odkształcenia traktowane są jako ciągłe funkcje czasu,
założenie ciągłości masy ruchy wszystkich elementów płynu są od siebie zależne,
założenie ciągłości odkształceń elementów płynu powstanie obok pola prędkości ruchu postępowego, pola prędkości obrotowych i pola prędkości odkształceń.
Zadania kinematyki :
określenie pola prędkości v,
określenie pola przyspieszeń a,
dla dowolnego elementu w dowolnym czasie.
Znajomość pola prędkości i przyspieszeń => wyznaczenie pola ciśnień p i gęstości.
Parametry ruchu płynów :
prędkość,
przyspieszenie,
ciśnienie.
Klasyfikacja przepływów :
Przepływ :
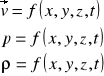
nieustalony (niestacjonarny) - parametry przepływu zależą od czasu i współrzędnych położenia,
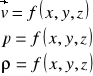
ustalony (stacjonarny) - parametry przepływu nie zależą od czasu lecz jedynie od położenia,
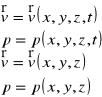
Przepływ trójwymiarowy :
nieustalony,
ustalony,
Przepływ dwuwymiarowy :
płaski - między dwiema równoległymi płaszczyznami, do których wektory prędkości są równoległe,
osiowosymetryczny - /v= v(r,z,t)/ wszystkie elementy płynu leżące na tym samym okręgu poruszają się z taką samą prędkością (np. przepływy w rurociągu, dyfuzory, dysze o przekroju kołowym, osiowy przekrój brył obrotowych).
Przepływ jednowymiarowy : parametry ruchu zależą od jednej współrzędnej /położenia/ - stosowany w obliczeniach hydraulicznych.
Analityczny opis przepływów :
metoda Lagrange'a - analiza wędrowna,
metoda Eulera - analiza lokalna.
Metoda Lagrange'a :
rozpatrujemy ruch elementów płynu wzdłuż ich toru,
elementy płynu charakteryzuje się za pomocą współrzędnych jakie posiadł w chwili t=t0.
Jest to metoda teoretyczna, gdyż ciężko jest śledzić konkretny element płynu.
Opisanie za pomocą równoważnego układu równań analitycznych :
Jeżeli t jest zmienną, to równania te stanowią równanie toru elementu płynu, który w chwili t=t0 przechodził przez punkt P0(a,b,c).
Jeżeli t jest stałą a współrzędne są zmiennymi to równania opisują przestrzenny rozkład elementów płynu w danej chwili t.
Wyróżniony element płynu
przebędzie drogę :
z prędkością :
wektorowe pole prędkości :
wektorowe pole przyspieszeń :
gdzie :
Metoda Eulera :
polega na badaniu zmian, jakim w czasie przepływu podlega prędkość elementu płynu, przepływający przez wybrany w obszarze poruszającego się płynu punkt,
opis parametrów zgodny ze sposobem prowadzenia bezpośrednich pomiarów,
pole prędkości :
czyli :
współrzędne Eulera :
wektor przyspieszeń pochodna zupełna wektora prędkości pochodna substancjalna :
- zmiana wektora prędkości wiąże się ze zmianą położenia dx, a zmiana położenia następuje podczas zmiany czasu dt.
pochodna pochodna
lokalna unoszenia
Pochodną substancjalną wyznacza się analogicznie dla pozostałych parametrów przepływu, zarówno dla wielkości wektorowych jak i skalarnych.
Tor i linia prądu :
Tor - droga jaką zakreśla element płynu w ruchu.
W metodzie Lagrange'a tor opisują równania 1-3 po wyeliminowaniu czasu.
W metodzie Eulera tor opisują równania różniczkowe trajektorii :
Linia prądu - jest to linia do której w danej chwili w każdym jej punkcie wektory prędkości elementu płynu, leżących na tej linii są styczne.
linie prądu nie mogą się krzyżować,
wyrażone dla dwóch różnych chwil na ogół się nie pokrywają.
Różniczkowe równania linii prądu.
Warunek styczności :
K - kontur - powierzchnia zawarta w obszarze linii prądu ale nie będąca linią prądu, to zbiór linii prądu tworzących powierzchnię, a poprowadzone przez każdy punkt konturu nazywamy rurką prądu, płyn wewnątrz to struga. Jeżeli ogranicza dowolną skończoną powierzchnię to rurkę prądu uogólniamy do powierzchni prądu. Strumień - płyn zawarty wewnątrz powierzchni prądu.
Przykład :
Dla przepływu płaskiego nieustalonego opisanego funkcjami vx=x+t, vy=y+t, określić :
linię prądu przechodzącą w t=0 przez punkt A(1,1),
tor tego elementu płynu, który w chwili t=0 znajdował się w punkcie A
Równanie linii prądu :
całkując :
dla :
zatem równanie linii prądu przechodzącego w chwili t=0 przez punkt A to :
x = y
Mechanika Płynów - Wykład 7
- 2 -
![]()
![]()
![]()
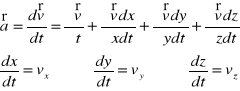
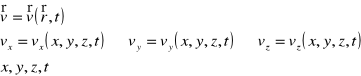
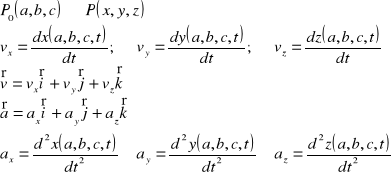
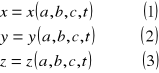
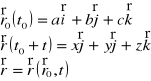
z
P0(t0)
r0
r P(t0+t)
k c z
i j a x y
b
x y
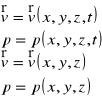
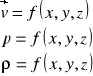
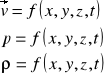
z
v
ds
K
k
i j y
x
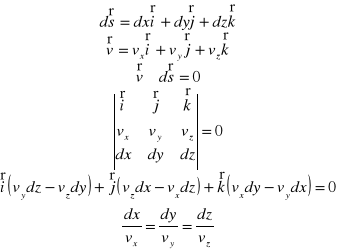
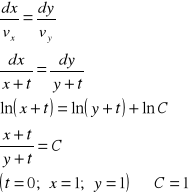
Wyszukiwarka
Podobne podstrony:
Koral 13, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Koral 14, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Koral 17, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Koral 11, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Koral 19, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Koral 15, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Koral 12, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Koral 10, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Newton jest jak Herkules z bajki, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
PLYNY4~1, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Podstawowe charakterystyki temperatury powietrza, Księgozbiór, Studia, Mechanika Płynów i Dynamika G
ruch laminarny2, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
POLITE~2, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
więcej podobnych podstron