Marek Kopyto
Nr indeksu : 94597
Wprowadzenie do systemów telekomunikacyjnych
Seminarium rok 2000/2001
Zadanie 1/7
1) Treść zadania:
Znaleźć transformaty Fouriera, wykorzystując jej własności, następujących funkcji:
a) f{t}
A
-2 -1 1 2
t
A/2
rys.1
b) g(t)
A
t
-2 0 1
rys.2
c)
h(t)
A
cos t
- π/2 π/2
rys.3
2) Wprowadzenie teoretyczne:
Ciągła transformata Fouriera jest przekształceniem całkowym opisanym wzorem:
![]()
gdzie: f(t) - sygnał, którego transformatę wyznaczamy
ω - pulsacja sygnału
Własności ciągłej transformaty Fouriera:
liniowość
F{a*f(t) + b*h(t)}= a*F{f(t)} + b*F{h(t)}
transformata pochodnej funkcji:
![]()
)
przesunięcie w czasie:
F{f(t-to) = e-jωto *F{f(t)}
splot funkcji:
![]()
3) Rozwiązanie:
W celu wyznaczenia transformat podanych wyżej przebiegów skorzystam z własności liniowości oraz transformaty pochodnej funkcji
a) Różniczkując sygnał podany na rys.1 otrzymuję następujący przebieg
A f `(t)
-2 -1,5 0 1,5 2 t
-A
Sygnałowi przedstawionemu na rysunku odpowiada transformata F{jω}*jω, gdzie F{jω} transformata sygnału f(t).
Różniczkując drugi raz otrzymujemy
2Aδ(t +1,5 ) f`(t) 2Aδ(t - 1,5 )
2A
-2 -1,5 0 1,5 2
t
-A
-Aδ(t +2 ) -Aδ(t - 2)
-2A -2Aδ(t)
Z kolei temu sygnałowi odpowiada transformata -ω2 F(jω).
Czyli:
![]()
Korzystając również z faktu, że:
F{δ(t)}=1 oraz z własności o przesunięciu w czasie, możemy napisać :
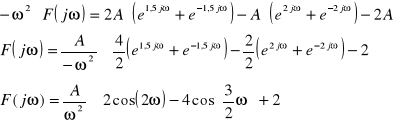
b) Podobnie postępując jak w przykładzie a) z sygnałem przedstawionym na rys. 2 otrzymujemy:
g `(t)
A/2
-2 0 1 t
-A
Sygnałowi temu odpowiada transformata jωF{g(t)) gdzie g(t) sygnał przedstawiony na rys.2.
Różniczkując po raz drugi otrzymujemy:
g ``(t)
Aδ(t - 1)
0,5Aδ(t + 2)
-2 0 1 t
-1,5 Aδ(t)
Z kolei temu sygnałowi odpowiada transformata -ω2 F(jω).
Czyli:
![]()
Korzystając również z faktu, że:
F{δ(t)}=1 oraz z własności o przesunięciu w czasie, możemy napisać :
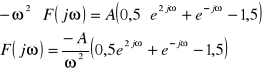
c) Różniczkując sygnał przedstawiony na rys.3 otrzymujemy:
h`(t)
A
-Asint
π/2
-π/2 0 t
-A
Sygnałowi temu odpowiada transformata jωF{h(t)) gdzie h(t) sygnał przedstawiony na rys.3.
Różniczkując po raz drugi otrzymujemy:
g``(t)
A Aδ(t + π/2 ) Aδ(t - π/2 )
-π/2 π/2 t
-Acost
-A
Sygnał ten możemy zapisać:
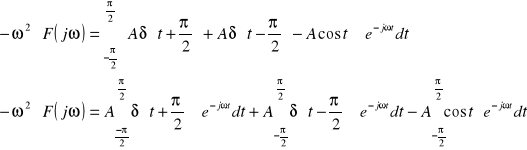
Ponieważ:
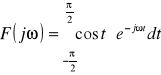
to:
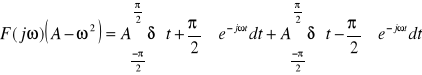
Korzystając również z faktu, że:
F{δ(t)}=1 oraz z własności o przesunięciu w czasie, transformacie pochodnej funkcji oraz własności liniowości możemy napisać :
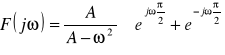
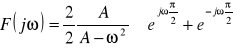
Ponieważ:
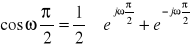
to ![]()
4)Wnioski:
Ciągła transformata Fouriera jest typem analizy widmowej.
Stosując różniczkowanie oraz korzystając z innych podstawowych własności tej transformacji można dosyć szybko i skutecznie określić widmo amplitudowe oraz fazowe badanego sygnału. Przy czym widmo amplitudowe jest modułem z transformaty Fouriera, a widmo fazowe argumentem tej transformaty.
3
Wyszukiwarka
Podobne podstrony:
pomoc2cd(1), SPRAWOZDANIA czyjeś
Budowa kontenera C, SPRAWOZDANIA czyjeś
Zalety systemów SDH, SPRAWOZDANIA czyjeś
Hartowanie i odpuszczanie, SPRAWOZDANIA czyjeś
z3 06, SPRAWOZDANIA czyjeś
Zabezpieczenie transformatora za pomocą zespołu automatyki(1), SPRAWOZDANIA czyjeś
w4m, SPRAWOZDANIA czyjeś
Z5 10, SPRAWOZDANIA czyjeś
pomoc, SPRAWOZDANIA czyjeś
siwex, SPRAWOZDANIA czyjeś
MetodyNumeryczne, SPRAWOZDANIA czyjeś
pomoc2, SPRAWOZDANIA czyjeś
labelektr14, SPRAWOZDANIA czyjeś
Budowa kontenera VC, SPRAWOZDANIA czyjeś
z4 06, SPRAWOZDANIA czyjeś
Kształtowanie widma, SPRAWOZDANIA czyjeś
Z2 08, SPRAWOZDANIA czyjeś
z4 02, SPRAWOZDANIA czyjeś
więcej podobnych podstron