2 Promieniowanie Róntgena. Określanie położenia defektów w ciałach stałych

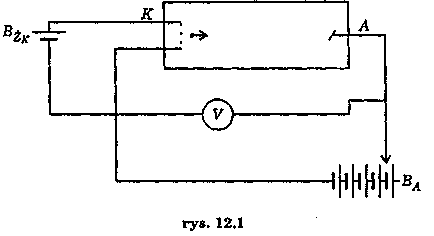
Promieniowanie rentgenowskie wytwarza się w tzw. lampach rentgenowskich, których schemat jest przedstawiony na rysunku 12.1.

Nazwanie przez Roentgena odkrytych przez siebie promieni promieniami X, pochodzi stąd, iż nie potrafił on określić czynnika, który powoduje ich powstawanie. Roentgen ustali} następujące właściwości odkrytych promieni:

- promienie rozchodzą się po liniach prostych,

— nie niosą ze sobą ładunku.

HAGA i WIND wykazali, że promienie te mają cechy ruchu falowego, nato­miast BARKLA stwierdził, że są to fale poprzeczne. THOMSON uważał, że są promieniowaniem elektromagnetycznym o dokładnie takiej samej naturze co światło widzialne, tylko o znacznie krótszych długościach fali. Uzasadnił to następująco: promienie rentgenowskie muszą być falą elektromagnetyczną, po­nieważ powstają w miejscu, gdzie elektrony uderzają o ścianki lampy katodo­wej, doznając przy tym bardzo dużego przyspieszenia hamującego.

W lampie rentgenowskiej katoda charakteryzuje się dużą zdolnością termoemisji. Gęstość tego prądu jest bardzo duża i określona wzorem Ri-chardsona.

(12.1)

gdzie:

W — praca wyjścia, k — stała Boltzmanna, T - temperatura.

Pod wpływem napięcia anodowego powstaje pomiędzy anodą i katodą

pole elektryczne, które działa na elektrony siłą F=eE, pod której wpływem doznają one przyspieszenia:

(12.2)

Inaczej mówiąc pole elektryczne powoduje wzrost energii kinetycznej elek­tronów, zgodnie z wyrażeniem:

(12.3)

Przy anodzie uzyskują one bardzo dużą prędkość, określoną wyrażeniem:

(12.4)

Gdy napięcie zasilające lampę U_a = 30000 V, prędkość elektronów docie­rających do anody wynosi 1/3 c. Napięcie, jakie stosuje się w lampach rent­genowskich, wynosi od 20 kV do 250 kV. Elektrony o tak dużej energii po dojściu do anody podlegają dwom procesom:

− rozpraszaniu na materiale anody,

− zderzeniom z elektronami atomów anody.

Rozpraszanie elektronów zachodzi wskutek oddziaływania kulombow-skiego przy zderzeniach z jądrami atomów anody. W jednym zderzeniu tego rodzaju padający elektron doznaje dużych przyspieszeń skierowanych przeciw­nie do kierunku ruchu i może ulec rozproszeniu pod dużym kątem. Zarówno fizyka klasyczna, jak i kwantowa przewidują w takim przypadku emisję pro­mieniowania elektromagnetycznego przez rozpraszane elektrony. W teorii kla­sycznej małe ilości promieniowania są emitowane jak to wynika z równań Maxwella, przez cały czas, jeżeli naładowana cząstka doznaje przyspieszenia. Wypromieniowywanie energii przez cząstkę naładowaną ładunkiem n e, która doznaje przyspieszenia a, będzie zachodziło z szybkością:

(12.5)

gdzie:

c - prędkość światła.

Gdy taka cząstka jest rozpraszana przez jądro, wówczas działają na nią siły Coulomba proporcjonalne do

n Z e².

Jeżeli masa jej wynosi m, to przyspieszenie, jakiego doznaje, jest proporc­jonalne do nZe²/m. Wobec tego szybkość wypromieniowywania energii wynosi

(12.6)

Czynnik m w mianowniku wskazuje, że emisja promieniowania elektromag­netycznego jest odwrotnie proporcjonalna do masy cząstki naładowanej, nato­miast czynnik Z² (liczba atomowa materiału anody) informuje, że anody wyko­nane z materiałów o większym Z są bardziej wydajne.

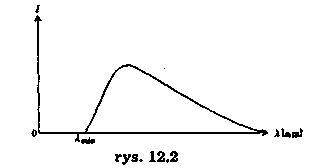
Ponieważ elektrony, docierające do anody ulegają rozproszeniu pod róż­nymi kątami, doznają różnego oddziaływania z jądrami atomów anody, więc emitowana energia ma widmo ciągłe (rys. 12.2).

Powstałe na tej drodze promieniowanie nazywa się promieniowaniem hamo­wania. Cechą tego promieniowania jest to, że rozkład widmowy nie zależy od materiału, z jakiego jest wykonana anoda lampy, a jedynie od wartości napię­cia anodowego. Na rysunku 12.3 pokazano jak wygląda według fotonowej teorii promieniowania elementarny proces, odpowiedzialny za powstawanie promieniowania o widmie ciągłym.'

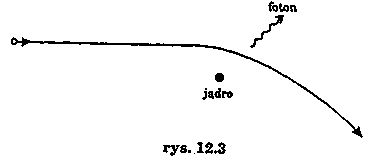
Elektron o początkowej energii kinetycznej E_o w wyniku oddziaływania z cięż­kim jądrem atomu anody doznaje hamowania i energia, którą wówczas traci, pojawia się w formie kwantów-fotonów promieniowania rentgenowskiego. Oznaczając energie kinetyczną elektronu po zderzeniu jako E, otrzymuje się następujący wzór na energię powstającego fotonu:

(12.7)

W wyniku zderzeń elektrony wiązki padającej mogą tracić różne ilości energii i w typowym przypadku pojedynczy elektron zostaje spowolniony, aż do za­trzymania dopiero w rezultacie wielu zderzeń z jądrami atomów anody. Wobec tego promieniowanie rentgenowskie wytworzone przez wiele elektronów bę­dzie miało Widmo ciągłe, takie jak na rysunku 12.2. Inaczej mówiąc, powstaje wiele fotonów, których długości fal są zawarte w przedziale od λ _min do λ= ∞, co odpowiada występowaniu różnych wartości strat energii w zderzeniach. Foton o najmniejszej długości fali będzie emitowany wtedy, gdy elektron straci całą swoją energię kinetyczną w jednym zderzeniu hamującym jego ruch. W ta­kim przypadku E = 0, a więc E_o = hc/λ_min. Korzystając ze wzoru (12.3), można napisać, że:

(12.8)

stąd wyrażenie na krótkofalową granicę promieniowania ciągłego jest nastę­pujące:

(12.9)

Najmniejsza długość fali w ciągłym promieniowaniu rentgenowskim od­powiada zamianie całej energii kinetycznej elektronów na promieniowanie. Ze wzoru (12.9) wynika, że jeżeli h= 0, to i λ_min=0, tak jak przewiduje teoria klasyczna. Świadczy to o tym, że wystosowanie w widmie ciągłym pewnej minimalnej długości fali jest zjawiskiem kwantowym. Promieniowanie hamo­wania powstaje nie tylko w lampach rentgenowskich, ale zawsze wtedy, gdy szybkie elektrony zderzają się z materią. Na przykład w promieniowaniu kos­micznym promieniowanie hamowania jest generowane w obszarze tzw. pasów van Allena otyczających Ziemię. Powstają one także przy zatrzymywaniu elek­tronów wychodzących z akceleratorów lub wysyłanych przez jądra promienio­twórcze.

W drugim przypadku elektrony o bardzo dużej energii wnikają w głąb atomów anody i w wyniku kulombowskiego oddziaływania może dojść do zderzeń niesprężystych z elektronami związanymi (na głębszych powłokach) atomów anody. Elektrony atomowe w tym zderzeniu mogą uzyskać energię większą od energii oddziływania z jądrem i opuścić macierzysty atom. W tym przypadku zachodzi tzw. głęboka jonizacja atomów. Na miejsce po takim elek­tronie przechodzi elektron z wyższego poziomu, wypromieniowując — zgodnie z drugim postulatem Bobra — kwant energii. W zależności od głębokości jonizacji (orbity, z której zostaje uwolniony elektron), jednemu zderzeniu może odpowiadać kilka kwantów energii. Np. jeżeli anoda jest wykonana z atomów, w których elektrony walencyjne znajdują się na orbicie O i zostanie uwolniony

elektron z orbity K, to zostaną wyemitowane cztery kwanty energii (hν_LK, hν_ML. hν_NM i hν_ON). W ten sposób powstaje liniowe widmo rentgenowskie, zwane charakterystycznym, które ujawnia się na tle widma ciągłego w postaci linii o bardzo dużym natężeniu (rys. 12.4).

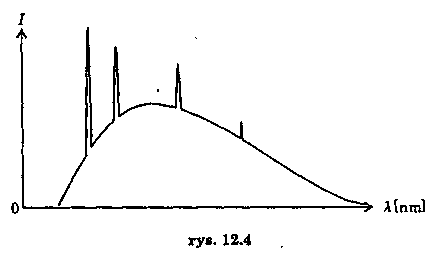
Widmo to nazywa się charakterystycznym, ponieważ zależy od materiału, z ja­kiego jest wykonana anoda lampy.

Cechą rentgenowskich widm liniowych jest regularność zmian częstotliwo­ści i długości fali linii od pierwiastka do pierwiastka. Przyczyną tej regularności jest zależność charakterystyk widm rentgenowskich od energii wiązania elek­tronów w powłokach wewnętrznych. Ta regularność została po raz pierwszy zaobserwowana przez MOSELEYA. Zależność liczby falowej w funkcji liczby atomowej pierwiastka, dla charakterystycznych serii K_α różnych pierwiastków, nosi nazwę prawa Moseleya.

Promieniowanie rentgenowskie

— wykazuje dużą zdolność jonizującą,

— jest bardzo przenikliwe,

— wywołuje zjawisko fotoelektryczne u wszystkich ciał,

— działa szkodliwie na organizmy żywe.

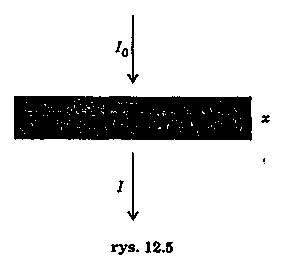
Promieniowanie rentgenowskie o natężeniu /_o padając na dowolne ciało ulega pochłanianiu i rozproszeniu. Natężenie promieniowania rentgenowskie­go o natężeniu /_o po przejściu przez ciała o grubości x (rys. 12.5) maleje wg. wzoru:

(12.10)

Współczynnik μ nazywa się współczynnikiem pochłaniania. W przypadku pro­mieniowania rentgenowskiego wyróżnia się współczynnik pochłaniania maso­wy μ_m atomowy μ_a. Masowy współczynnik definiuje się jako:

(12.11)

gdzie:

a - wartość stała zależna od liczby Ayogadro N₀ i masy atomowej Ą

p - gęstość bezwzględna ciała pochłaniającego.

Atomowy współczynnik pochłaniania jest określony następująco:

(12.12)

Pochłanianie promieniowania rentgenowskiego jest właściwością atomową, nie zaś cząsteczkową materii. Atomowy współczynnik μ_a nie zależy od rodzaju związku, w którego skład wchodzi dany atom. Rozpraszaniem promieniowania rentgenowskiego zajmował się BRAGG, który otrzymał następujące wyrażenie na długość fali rozproszonej:

(12.13)

gdzie:

m - krotność długości fali rozpraszanej,

d — stała sieci krystalicznej ciała rozpraszającego,

Φ— kąt odbłysku promienia od płaszczyzny węzłowej.

---