Tchórzewski Seweryn

Wodarski Krzysztof

Podstawy Projektowania Inżynierskiego

Przewodnik po ćwiczeniach

Motto:

Myślenie Projektowe:

Tak długo udoskonalać pomysł,

Aż uzyska się zamierzony efekt

Zabrze 2000

Druk: Profil-Druk; tel. [phone]

Ul. Dolnej Wsi 2, Gliwice

Skład: YETI Media

Spis ćwiczeń

Lp.	Temat	Data	Podpis	Strona
Metody heurystyczne
1	Burza mózgów			8
2	Superpozycja			12
3	Analiza połączeń			16
4	Morfologia			20
5	Algorytmizacja zadań			32
Optymalizacja w projektowaniu
6	Analiza matematyczna			45
7	Systematyczne przeszukiwanie			53
8	Programowanie dynamiczne			60
9	Programowanie sieciowe			71
Projektowanie a ekonomiczna efektywność inwestycji
10	Rachunek aktualizacji			87
11	Próg rentowności			100
12	Okres zwrotu nakładów, wartość kapitałowa			109
Ocena końcowa:

Metody Heurystyczne

Wprowadzenie do ćwiczeń od 1 do 4

Celem ćwiczeń od 1 do 4 jest przedstawienie ogólnych heurystycznych metod wspomagających proces poszukiwania możliwych rozwiązań danego zadania w projektowaniu technicznym. Należy podkreślić, że przedstawione metody znajdują także zastosowanie w innych rodzajach projektowania, np. dla rozwiązywania problemów organizacyjnych, reklamowych i innych. Przed przystąpieniem do koncypowania, czyli do poszukiwania zbioru rozwiązań, należy sformułować zadanie projektowe. Zadanie projektowe jest często dane w postaci problemu projektowego. Dla porządku należy przybliżyć oba te pojęcia [5],[16],[17]:

problem - to początkowa postać sformułowania potrzeby, która ma zostać zaspokojona w procesie projektowania, zaś zadanie, to konkretny opis tego, co ma zostać rozwiązane w danym procesie projektowania. Można przyjąć, że zadanie jest sformułowane za pomocą:

• opisu wejść i wyjść projektowanego obiektu,

• systemu wartości potrzebnych do oceny jego jakości,

• zbioru wymagań i ograniczeń.

Formułowanie zadania projektowego jest pierwszym i ogromnie ważnym działaniem w procesie projektowania. Jest bowiem oczywiste, że taki problem będzie rozwiązany, jaki został postawiony. A zatem jakość rozwiązania zależy od jakości sformułowanego zadania projektowego.

Formułowanie zadania projektowego koncentruje się na następujących celach:

• określeniu istoty potrzeby, jaka ma zostać zaspokojona przez wytwór projektowania (funkcje obiektu), czyli określenie celu projektowania,

• uogólnieniu i konkretyzacji potrzeby, w porównaniu ze sformułowaniem danym na początku,

• poszerzeniem obszaru poszukiwań,

• eliminacją wymagań pozornych,

• transformacją zadania do takiej postaci, w której łatwiej jest rozwiązywalne lub transformacja do postaci bardziej adekwatnej do potrzeby.

Proces formułowania zadania projektowego jest heurystycznym działaniem, które dotychczas nie znalazło metod wspomagających. Można podać jedynie kilka zasad ułatwiających ten proces:

1. zadanie powinno być sformułowane jak najogólniej,

2. sformułowanie powinno być sformułowanie możliwie konkretnie,

3. sformułowanie nie powinno implikować żadnego rozwiązania,

4. zadanie powinno być sformułowane przez podanie funkcji, jaką obiekt ma pełnić, a nie za pomocą jego nazwy,

5. wygodne może okazać się określenie dwóch stanów, tzn. przed i po zaspokojeniu potrzeby.

Znajdowanie rozwiązań projektowych, dla postawionego problemu i zadania projektowego może być wspomagane wieloma metodami heurystycznymi. Niniejszy skrypt przedstawia wybrane metody heurystyczne, wspomagające proces poszukiwania możliwych rozwiązań danego zadania w projektowaniu technicznym.

Ogólnym celem metod heurystycznych jest wspomaganie intelektualnego twórczego wysiłku projektanta, a nie wyeliminowanie człowieka z procesu twórczego i automatyzacja tego procesu. To wspomaganie osiąga się przez spowodowanie odpowiedniej postawy twórczej, w szczególności przez:

• pokonanie psychicznych i organizacyjnych barier w procesie twórczym,

• stymulowanie i wykorzystanie podświadomej pracy mózgu,

• umożliwienie wglądu w proces twórczy, jego rejestracja i kontrola,

• oddzielenie procesu generowania pomysłów i ich oceny,

• umożliwienie współpracy w grupie,

• umożliwienie efektywnej pracy twórczej osobom o mniejszej wyobraźni, fantazji, pomysłowości, zdolności kojarzenia i itp.

Ćwiczenie nr 1

Burza mózgów. Metoda 635

Cel laboratorium:

Zastosowanie metody burzy mózgów w procesie projektowym. Zastosowanie metody 635 (jako odmiany metody burzy mózgów) w procesie projektowym. Rozwiązywania problemu w grupie. Znajdowania dużej liczby rozwiązań projektowych.

Burza mózgów

Istota metody

Burza mózgów - sprowadza się do znalezienia w stosunkowo krótkim czasie, przez zespół kilku lub kilkunasto osobowy, rozwiązań dla postawionego problemu. Uczestnicy sesji burzy mózgów formułują możliwie długą listę wariantów (pomysłów) rozwiązania z wyłączeniem krytyki hamującej twórczą inwencję.

Grupę organizuje się doraźnie. Oprócz specjalistów z danej dziedziny mogą być laicy - ludzie z „otwartą głową”. Do 6 osób, 40-60 minut, mentor grupy.

Zasady sesji realizacji:

1. Pod żadnym pozorem nie jest dozwolona krytyka podawanych pomysłów.

2. Prowadzący sesję może i powinien sam zgłaszać pomysły oraz zachęcać uczestników do wykorzystywania wcześniej zgłoszonych pomysłów, np. przez ich modyfikację albo łączenie w nowe całości.

3. Efektem sesji powinna być duża liczba pomysłów, natomiast ich jakość nie jest w czasie sesji w ogóle analizowana.

4. Jeśli prowadzący sesję zauważa, że strumień zgłaszanych pomysłów maleje, może zastosować inne znane techniki stymulacji: np. analogi synektyczne, biosocjację, itp.

Przebieg ćwiczenia

Sesja powinna mieć swobodną i nieoficjalną atmosferę. Wśród uczestników nie może osoby o przytłaczającym autorytecie. Należy starać się o nastrój przyjemności i zabawy. Sekretarz (lub magnetofon) rejestruje na bieżąco zgłaszane pomysły. Tym lepiej, im pomysłów jest więcej i im są dziwniejsze i bardziej ekstrawagandzkie. Każda idea jest pożądana, ponieważ stymuluje innych uczestników, a potem projektanta. Otrzymany zbiór pomysłów traktuje się jako „surowy” materiał stymulujący projektanta do rozszerzania jego horyzontów i zbudowania pewnej przestrzeni rozwiązań. Zbiór ten jest po sesji porządkowany i krytycznie analizowany (np. za pomocą metod klasyfikacji, morfologii, drzewa rozwiązań).

Sesja może przebiegać w sposób spontaniczny, niekierowany, lub może być przeprowadzona przez przewodniczącego, w pewnych kolejnych etapach, np.:

1. stawianie i określenie zadania,

2. generowanie pomysłów, ulepszanie pomysłów,

3. porządkowanie i wartościowanie (wstępne) rozwiązań.

Metoda „635”

Metoda 635 jest odmianą burzy mózgów. Każdy z uczestników ćwiczenia powinien wygenerować trzy rozwiązania dla zadanego problemu. Rozwiązania te muszą być zapisane na kartkach. Następnie rozwiązania te są przekazywane kolejno innym uczestnikom sesji dla ich uzupełnienia, wzbogacenia lub modyfikacji. Nazwa metody pochodzi stąd, że przy 6 uczestnikach, każda kartka z 3 pomysłami jest uzupełniana przez 5 pozostałych uczestników.

Ćwiczenie

1. Każdy uczestnik musi wygenerować trzy rozwiązania zadanego problemu. Pomysły uczestników muszą zostać zapisane w formularzu (5-10 minut).

2. Po tym czasie uczestnicy zespołu wymieniają się formularzami,

3. Uczestnicy sesji starają się rozwinąć i zmodyfikować otrzymane pomysły,

4. Wymiana formularzy trwa tak długo, aż kartki przejdą przez ręce wszystkich członków zespołu (około 20 minut).

Propozycje problemów do rozwiązania:

1. urządzenie do odśnieżania ulic,

2. zabezpieczenie garażu przed włamywaczami,

3. urządzenie (lub sposób) do kontroli uiszczenia opłaty za przejazd w autobusach,

4. zabezpieczenia samochodu przed złodziejami,

5. ograniczenie ilości śmieci,

6. transport osobowy w mieście,

7. przechowywanie informacji,

8. opakowania na żywność,

9. sposób kontroli wykonywania czynności zawodowych przez pracowników,

10. sposób zagospodarowania odpadów, np. starych opon itp.

Zadanie do wykonania

Znajdowanie rozwiązań metodą 635

Problem:.................................................................................................................................................

.................................................................................................................................................................

Propozycje rozwiązań problemu

Rozwiązanie 1 :......................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Uwagi :...................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Rozwiązanie 2 :......................................................................................................................................

.................................................................................................................................................................

................................................................................................................................................................

Uwagi :...................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Rozwiązanie 3 :......................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Uwagi :...................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Ćwiczenie nr 2

Superpozycja

Cel laboratorium:

Zastosowanie metody superpozycji w procesie projektowym. Rozwiązywania problemu w grupie. Wykorzystanie metody analogii dla znajdowania rozwiązań projektowych.

Istota metody.

Metoda superpozycji jest metodą stymulacji myślenia twórczego, wymuszającą kojarzenie idei, pomysłów, metod itp. po to, aby w ten sposób zwiększyć prawdopodobieństwo znalezienia nowej idei pomysłu, rozwiązania, metody itp. Punktem startowym tej metody jest problem do rozwiązania lub konkretna konstrukcja (czy metoda) do ulepszenia. Pierwszym krokiem jest wybranie na chybił trafił kilku obiektów, można do tego użyć np. encyklopedii lub słownika, dowolnie wybierając hasła, albo zaproponować dowolne elementy spośród widzianych w najbliższym otoczeniu. Następnie należy wymienić kolejno różne cechy tych obiektów, (dotyczące budowy, właściwości użytkowych, wyglądu, skojarzeń nimi wywołanych) zestawiając je z badanym problemem, próbując znaleźć nowe skojarzenia, ukazujące badany problem w nowym świetle.

Przykład

Przedmiotem projektu jest lekka przenośna ścianka działowa używana do doraźnego dzielenia pomieszczeń na mniejsze wnętrza. Celem jest określenie materiału, konstrukcji i sposobu montażu ścianki.

Obiekty pomocnicze to: notes, żaluzja, papierosy, szklanka, wiatr, lampa kreślarska.

Opis obiektów:

Notes: papierowy, prostopadłościan, czarny w plastikowej folii, kieszonkowy, wiele warstw papieru.

Rozwiązania: ścianka z papieru w ramkach (jak w Japonii), ścianka typu „plaster miodu”, rozwijana z folii plastikowej.

Żaluzja: podnoszona na sznurkach, z listewek, zawieszona na prętach, składana.

Rozwiązania: można w całości przejąć ideę konstrukcyjną żaluzji.

Papierosy: okrągłe, niebezpieczne dla zdrowia, tytoń w rurce.

Rozwiązania: drewniane lub papierowe (plastikowe) elementy wypełniane materiałem izolacyjnym.

Szklanka: szklana, okrągła, przeźroczysta.

Rozwiązania; brak

Wiatr: ruch powietrza, zimno.

Rozwiązania: ścianka z elementów pneumatycznych lub mocowana na przyssawki.

Lampa kreślarska: światło, ciepło, mocowana imadełkiem do deski, na przegubach.

Rozwiązania: mocowana przez rozpór do podłogi i sufitu, składana przegubowo.

Zadanie do wykonania

Przykładowe problemy do rozwiązania:

1. Zabezpieczenie garażu przed złodziejami.

2. Zabezpieczenie roślin przed szkodnikami.

3. Zabezpieczenie wejścia do domu.

4. Zabezpieczenie samochodu przed kradzieżą.

5. Dystrybucja towarów.

6. Komunikacja między ludźmi - przepływ informacji.

7. Oświetlenie pomieszczenia.

Zadanie:

należy znaleźć nowe rozwiązanie (materiał, konstrukcja, sposób montażu itp.) dla:

.................................................................................................................................................................

Obiekty pomocnicze:

1. ....................................................................................

2. ....................................................................................

3. ....................................................................................

4. ....................................................................................

5. ....................................................................................

ad 1. .......................................................................................................................................................

Cechy obiektu: .......................................................................................................................................

.................................................................................................................................................................

Rozwiązanie: ..........................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

ad 2. .......................................................................................................................................................

Cechy obiektu: .......................................................................................................................................

.................................................................................................................................................................

Rozwiązanie: ..........................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

ad 3. .......................................................................................................................................................

Cechy obiektu: .......................................................................................................................................

.................................................................................................................................................................

Rozwiązanie:...........................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

ad 4. .......................................................................................................................................................

Cechy obiektu: .......................................................................................................................................

.................................................................................................................................................................

Rozwiązanie: ..........................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

ad 5. .......................................................................................................................................................

Cechy obiektu: .......................................................................................................................................

.................................................................................................................................................................

Rozwiązanie: ..........................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Ćwiczenie nr 3

Poszukiwanie nowych połączeń i nowych zależności

Istota tej metody to strukturalizacja zadania, tzn. podział zadania na elementy i określenie relacji między tymi elementami.

W zależności od rodzaju zadania (czy to problem, czy zadanie projektowe, czy zadanie typu ulepszania istniejącego obiektu) strukturę taką tworzy się „od nowa” lub stara się wykryć obiektywnie istniejącą strukturę i ją zmienić. Należy podkreślić, że podział zadania jest czynnością bardzo heurystyczną, tzn. w tym samym obiekcie można określić kilka różnych struktur, zależnie od przyjętego kryterium podziału.

W metodzie tej uzyskuje się wynik wstępny, „surowy”, który podlega dalszej ocenie. Zależnie od merytorycznej treści problemu projektant ocenia ten wynik, wprowadzając ewentualne dalsze wymagania (lub ograniczenia) i sprawdza otrzymany wynik ze względu na inne wymagania, których nie dało się sformalizować (np. wymagania estetyczne).

Jeśli otrzymane rozwiązanie nie może być z pewnych przyczyn zaakceptowane i nie możemy go poprawić, odpowiednio korygujemy założenia początkowe.

Inną klasą zadań w których metoda może zostać zastosowana jest układanie planów lub harmonogramów złożonych procesów, np. proces technologiczny montażu przyrządu produkowanego w wielkich seriach (np. zegarek, aparat fotograficzny), sterowanie ruchem wagonów, organizacja stanowisk w rozdzielni przesyłek na poczcie lub w banku.

Czynności realizowane w metodzie:

1. Dany problem (albo obiekt) dzieli się na części: definiuje się elementy i definiuje się relacje pomiędzy nimi.

2. Zestawia się kolejno elementy każdy z każdym i badamy jakie relacje zachodzą między nimi (lub jakie powinny zachodzić) , używając katalogu relacji (np. relacje funkcjonalne, typologiczne, relacje kolejności itp.)

3. Jeśli relacji nie ma - wprowadza się je i analizuje, co to może dać?

4. Jeśli relacje są - usuwa się i analizuje skutek, ewentualnie zmienia się rodzaj relacji.

Zadania do wykonania

Ćwiczenie pokazuje iteracyjny charakter procesu projektowego, tzn. wielokrotne analizowanie i doskonalenie zadania projektowego. Co istotne, powyższa metoda umożliwia rozwiązanie zadań przez ich strukturalizację, tzn. podział zadania na elementy i określenie relacji między tymi elementami.

Przebieg ćwiczenia:

1. Wyróżnienie poszczególnych elementów w obiekcie (minimum 6-7).

2. Tworzenie macierzy relacji pomiędzy elementami.

3. Przedstawienie macierzy relacji w postaci grafu połączeń.

4. Przekształcenie grafu połączeń w szkic rozwiązania lub obiektu.

Wybór obiektu do analizy spośród następujących propozycji:

• Hurtownia

• Firma transportowa

• Firma komputerowa

• Firma projektowa

• Hurtownia materiałów budowlanych

• Ośrodek szkoleniowy dla menedżerów

• Ośrodek odnowy biologicznej

• Salon kosmetyczny

• Restauracja szybkiej obsługi

Zadanie:

należy znaleźć rozmieszczenie pomieszczeń dla wybranego przykładu - .............................................

Wyróżnienie elementów (pomieszczeń)

Lp.	Nazwa pomieszczenia	Oznaczenie
1
2
3
4
5
6
7
8
9

Macierz relacji pomiędzy elementami (pomieszczeniami)

Oznacze.									Liczba punktów
	-
		-
			-
				-
					-
						-
							-
								-

Graf połączeń pomiędzy elementami

Przekształcenie grafu połączeń I

Przekształcenie grafu połączeń II

Projekt obiektu (rozmieszczenia elementów - pomieszczeń)

Ćwiczenie nr 4

Morfologia

Cel laboratorium:

Zastosowanie metody morfologicznej w procesie projektowym. Znalezienie nowych rozwiązań dla problemu, który już miał wcześniej rozwiązanie, ale uznaje się je za niezadowalające. Poszerzenie obszaru poszukiwań i wzbogacenie rozwiązań dopuszczalnych. Znalezienie pewnej systematyki zbioru rozwiązań dopuszczalnych, tzw. morfologii.

Szczegółowe cele metody:

1. stworzenie warunków obligujących twórcę do pełnego rozpoznania wymagań i ograniczeń i możliwie kompletnego sformułowania zadania,

2. zapobieżenie jednostronności i tendencyjności prowadzenia poszukiwań,

3. stworzenie warunków umożliwiających znalezienie nowych rozwiązań.

Istotą metody jest:

1. podział zadania (problemu) na podzadania (podproblemy), o mniejszym stopniu złożoności (wielowymiarowości), na niższym poziomie w hierarchii ogólności,

2. znajdowanie zbioru rozwiązań dla każdego z podzadań,

3. myślowe kombinatoryczne składanie (agregacja) tych podrozwiązań i w ten sposób uzyskiwanie zbioru rozwiązań całego problemu.

Procedura metody morfologicznej składa się z trzech etapów:

Po pierwsze - sformułowanie zadania - chodzi tu o zdefiniowanie zadania na podstawie danego problemu. Ten etap występuje w każdej metodzie. Służy do rewizji poprawności sformułowania problemu i przetransformowania go do nowej postaci tak, jak go rozumiemy i jak uważamy za słuszne ze względu na zaistniałą potrzebę. Nowe sformułowanie powinno być ogólne (lecz nie ogólnikowe), konkretne i pełne oraz adekwatne do rzeczywistej potrzeby.

Po drugie - wybór dziedziny rozwiązania i zakreślenie granic poszukiwanych rozwiązań - istniejące w każdym indywidualnym przypadku ograniczenia powodują, że arbitralnie określa się dziedzinę poszukiwań, a także wyznacza (choćby w sposób rozmyty) zakresy wartości poszczególnych zbiorów.

Po trzecie - strukturalizacja zadania - określenie jego morfologii jest działaniem heurystycznym i nie może być sformalizowane. Należy tu podzielić całe zadanie na istotne i niezależne podzadania.

Przykład

Aby metoda okazała się skuteczna, podział zadania musi być taki, aby poszczególne podproblemy były jednocześnie niezależne ale związane. O niezależności podproblemów mówi się wtedy, kiedy żadne z podrozwiązań dla jednego z podproblemu nie implikuje żadnego z podrozwiązań drugiego podproblemu.

Jeżeli zadaniem jest znalezienie możliwych konstrukcji pojazdu drogowego, mając w pamięci istniejące konstrukcje, np. samochodu, możemy zaproponować następujące morfologie:

P₁ - rozwiązanie podwozia,

P₂ - rozwiązanie nadwozia,

P₃ - rozwiązanie silnika,

P₄ - rozwiązanie układu kierowniczego, itd.

Możemy również zaproponować inną morfologię dla pojazdu:

P₁ - wnętrze pojazdu (różne warianty rozwiązania wnętrza,

P₂ - kształt i wygląd zewnętrzny,

P₃ - umiejscowienie silnika oraz pozostałych mechanizmów.

Pierwsza z morfologii przydatna byłaby dla konstruktora, druga zaś dla projektanta form oraz stylisty.

Przykład - dla dobrego podziału

Zadaniem jest dobór materiału do wykonania stołu. Podzieliliśmy go na dwa podzadania: P₁ - dobór materiału blatu, P₂ - dobór materiału nóg. Określamy następujące zbiory rozwiązań:

A₁ = {drewno, szkło, sklejka, marmur, tworzywo sztuczne, itd.},

A₂ = {drewno, metalowe pręty lub rurki, tworzywo sztuczne itd.}.

Przyjęty podział P = {P_1,P₂} jest niezależny (dobry), ponieważ każda kombinacja podrozwiązań jest fizycznie możliwa.

Przykład - dla złego podziału

Należy znaleźć koncepcję masowego transporty węgla z Górnego Śląska do Świnoujścia. Zadanie można podzielić na dwa podzadania:

P₁ - sposób transportu (droga), P₂ - środek transportu. Zaproponowano następujące rozwiązania częściowe:

A₁ = {szosa, kolej, transport wodny},

A₂ = {ciężarówki, wagony, barki}.

W tym przypadku przyjęcie a₁¹ implikuje a₂¹_, a przyjęcie a₁² implikuje a₂² itd., zatem zaproponowany podział <P₁ ,P₂> (czyli morfologia) jest nieodpowiedni, bo podrozwiązania są od siebie zależne.

Sposoby znajdowania morfologii.

Metoda pytań heurystycznych.

W zależności od tego, jakie aspekty problemy przyjmiemy za kryterium jego podziału powstają różne morfologie. Pomocne w zaproponowaniu morfologii może być jedno z następujących pytań:

• czym obiekt (czy rozwiązanie) ma być ?

• jakie części ma mieć ?

• jakie mam mieć właściwości ?

• jakie ma wykonywać funkcje ?

• w jaki sposób ma realizować swoje przeznaczenia ?

Przykład

Dla samochodu osobowego można zaproponować następujące morfologie:

P = {P₁, P₂, P₃, ...., P_m}

Wynikające z postawienia pytań:

czym obiekt (czy rozwiązanie) ma być ?

P_I = {środek transportowy, magazyn, mieszkanie campingowe, duma rodziny, itd.},

jakie części ma mieć ?

P_II ={dach, drzwi, silnik, oświetlenie, zawieszenie, itd.},

jakie ma wykonywać funkcje ?, w jaki sposób ma realizować swoje przeznaczenia?

P_III = {szybkość, zwrotność, estetyka, komfort, osłona przed warunkami zewnętrznymi, itd.}.

W celu lepszego zrozumienia można jeszcze zaproponować przykłady różnych morfologii dla mieszkania:

czym obiekt (czy rozwiązanie) ma być ?

P_I = {schronienie przed warunkami zewnętrznymi (klimatycznymi), schronienie przed innymi ludźmi (mój dom moim zamkiem [My Home Is My Castle]), magazyn rzeczy, miejsce wypoczynku, sny, rozrywki, itd.},

jakie części ma mieć ?

P_II ={kuchnia, łazienka, spiżarka, pokój I, pokój II, itd.},

jakie mam mieć właściwości ?

P_III = {zapewniać bezpieczeństwo, zabezpieczać odpowiedni standard - komfort (woda, ogrzewanie, prąd, ...), itd.}.

Metoda klasyfikacji.

Innym sposobem zbudowania pełnej morfologii może być metoda klasyfikacji, której celem jest stworzenie systematyki (uporządkowania według pewnej klasyfikacji) danego zbioru elementów. Ten zbiór może być rezultatem np. sesji burzy mózgów. Metoda jest realizowana w następujących krokach:

1. Generujemy zbiór „p” elementów (do dwudziestu) wchodzących w skład rozwiązania problemu P.

2. Zapoznajemy się ze zbiorem elementów.

3. Sortujemy elementy w różny sposób (zwykle na 3 do 6 grup), aż dojdziemy do zadowalającego nas układu. Taka klasyfikacja powinna zapewniać spełnienie następujących wymagań:

• idea klasyfikacji (kryterium podziałów) odpowiada naszej potrzebie,

• wszystkie elementy zostały sklasyfikowane,

• istnieje co najwyżej kilka elementów, które równie dobrze mogą być przydzielone do różnych grup,

• liczba grup jest pod naszą kontrolą,

• klasyfikacja zapewnia dobry punkt wyjścia do dalszych działań.

4. Określamy wyraźnie, jakie jest kryterium podziału.

5. Tworzymy brakujące grup tak, aby zbiór nazw grup był naszym zdaniem zbiorem zupełnym.

Przykład

Jak ochronić warsztat samochodowy przed pożarem ?

1. W wyniku burzy mózgów uzyskano następujące pomysły:

1. piorunochron,

2. beczka z wodą i skrzynia z piaskiem,

3. niepalne materiały budowlane,

4. „Precz z zapałkami”,

5. załoga warsztatu jest jednocześnie strażą pożarną,

6. automatyczne gaśnice,

7. cały budynek nakryć kocem gaśniczym.

2. Wstępnie klasyfikujemy według następujących grup:

• Grupa I - 1, 4;

• Grupa II - 3;

• Grupa III - 2,5,6,7.

3. Ujawniamy podział:

• Grupa I i II - niedopuszczenie do powstania pożaru,

• Grupa III - zmniejszenie skutków pożaru.

4. Możemy więc wykryć oraz uzupełnić brakujące grupy i zaproponować następujący podział:

• Grupa I - likwidacja źródeł ognia: iskier, płomienia, itd.,

• Grupa II - likwidacja materiałów palnych,

• Grupa III - obniżenie temperatury otoczenia,

• Grupa IV - szybkie gaszenie,

• Grupa V - zmniejszenie skutków pożaru: fizycznych (lokalizacja maszyn i urządzeń) oraz ekonomicznych (ubezpieczenie).

Podsumowanie:

Należy podkreślić, że metoda morfologiczna stanowi podstawową metodę poszukiwania rozwiązań zadań inżynierskich (choć często inżynier nie wie o metodzie, postępując zupełnie intuicyjnie) i dlatego warto poznać jej zasadę i właściwości.

Zaletą metody jest, że złożony wielowymiarowy problem zamieniony zostaje na szereg prostszych problemów, przy czym podział ten może być hierarchicznie kontynuowany, aż dojdzie się do tak niskiego poziomu ogólności pod-pod-zadań , że znalezienie dla nich rozwiązań nie jest trudne, a umożliwia to:

1. podział zadania (problemu) na podzadania (podproblemy), o mniejszym stopniu złożoności (wielowymiarowości), na niższym poziomie w hierarchii ogólności,

2. znajdowanie zbioru rozwiązań całego problemu,

3. myślowe kombinatoryczne składanie (agregacja) tych podrozwiązań i w ten sposób uzyskiwanie zbioru rozwiązań całego problemu.

Wadą metody jest, że dane jedno zadanie można dzielić różnie, zależnie od kryterium - a nie każdy podział jest przydatny, przy czym brak jest reguł podziału. Niedogodnością metody jest również to, że twórca musi wyobrazić sobie a priori rozwiązanie już w momencie startu po to, aby mógł je podzielić, albo przynajmniej wyrobić sobie jakiś pogląd choćby na strukturę zadania i strukturę rozwiązania.

Dodatkowo, pełne rozpoznanie morfologii problemu umożliwia przejście od projektowania koncepcyjnego do fazy projektowania technicznego (właściwego).

Zadania do wykonania

należy znaleźć nowe rozwiązanie dla:

.................................................................................................................................................................

.................................................................................................................................................................

Pytania heurystyczne:

1. Czym obiekt (rozwiązanie) ma być ?

2. Jakie ma mieć części ?

3. Jakie ma mieć własności i właściwości ?

4. Jakie ma wykonywać funkcje ?

5. W jaki sposób może realizować swoje przeznaczenie ?

Ad 1. ......................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Ad 2. ......................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Ad 3. ......................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Ad 4. ......................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Ad 5. ......................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Metoda klasyfikacji

Elementy morfologiczne:

1. .....................................................................	2. .....................................................................
3. .....................................................................	4. .....................................................................
5. .....................................................................	6. .....................................................................
7. .....................................................................	8. .....................................................................
9. .....................................................................	10. ...................................................................

Sortujemy elementy w odpowiednie grupy.

a) ............................................................................................................................................................

b) ............................................................................................................................................................

c) ............................................................................................................................................................

d) ............................................................................................................................................................

e) ............................................................................................................................................................

Uwagi:

Kryterium podziału (sposób sortowania) powinno odpowiadać określonej potrzebie.

Wszystkie elementy powinny być sklasyfikowane (przyporządkowane).

Może istnieć kilka elementów, które równie dobrze mogą być przydzielone do różnych grup

Określamy przyjęty podział grup oraz proponujemy brakujące grupy.

a) ............................................................................................................................................................

b) ............................................................................................................................................................

c) ............................................................................................................................................................

d) ............................................................................................................................................................

e) ............................................................................................................................................................

Algorytmy

Ćwiczenie nr 5

Algorytmizacja zadań

Cel laboratorium:

Zapoznanie z zasadami algorytmizacji zadań. Zastosowanie algorytmizacji w procesie projektowym.

Definicja algorytmu

Najczęściej stosowanych definicje pojęcia algorytm są następujące:

• (matem.) - dokładna recepta określająca proces obliczeniowy, który prowadzi od pewnych danych początkowych do żądanego rezultatu,

• zamknięty układ zależności logicznych, matematycznych lub obydwu razem, ustalający dokładny przepis jakiegoś działania, mówiąc inaczej uporządkowany zbiór operacji, taki, że po ich wykonaniu otrzymuje się rozwiązanie dowolnego zadania z określonej klasy zadań,

• przepis umożliwiający osiągnięcie danego celu (np. przepis kucharski podający opis czynności oraz składniki potrzebne do otrzymania żądanej potrawy, instrukcja obsługi jakiegoś urządzenia technicznego, wyznaczanie pierwiastków trójmianu kwadratowego - opisane językiem naturalnym: lista czynności przeznaczonych do wykonania na określonych obiektach, której wykonanie jest uwieńczone wynikiem.

Nieco inaczej brzmi definicja algorytmu podana przez Roberta Kowalskiego, jednego z współtwórców teorii programowania w logice [14]:

algorytm = logika + sterowanie

Przy czym przez logikę rozumie się tu związki logiczne zachodzące pomiędzy poszczególnymi obiektami występującymi w programie, przez sterowanie natomiast — proces wnioskowania na podstawie tych związków. Należy w tym miejscu dodać, że przyjmuje się, iż na program składają się dwa elementy: algorytmy i struktury danych.

Opisując algorytm należy wziąć pod uwagę, iż charakteryzuje się następującymi właściwościami:

1. ogólność - pozwala na rozwiązywanie określonej klasy zadań, a nie pojedynczego przypadku (rozwiązywanie równań różniczkowych 2 rzędu, a nie konkretnego równania),

2. skończoność - otrzymujemy rozwiązania po wykonaniu skończonej liczbie kroków (operacji),

3. określoność - wszystkie wykonywane operacje są jednoznaczne,

4. efektywność - czas potrzebny na wykonanie algorytmu ulega skróceniu w przypadku dużej powtarzalności procesu,

W przypadku gdy:

• dane trzeba przetwarzać masowo,

• przetwarzanie bez komputera trwałoby bardzo długo,

• wykonywanie zadań powtarza się.

wskazane jest skorzystanie z komputera. Algorytm umożliwia wówczas sprawne opracowanie programu realizującego opisane nim zadanie, a co za tym idzie skrócenie czasu realizacji całego procesu.

Algorytm może być opracowany w różnej formie:

1. Algorytm ogólny, który podaje kolejne etapy działania w ogólnym ujęciu - język formalny (język naturalny lub notacja).

2. Algorytm logiczny, który powstaje przez uzupełnienie algorytmu ogólnego zdarzeniami logicznymi.

3. Algorytm logiczno - matematyczny, który jest rozwinięciem algorytmu ogólnego lub algorytmu logicznego o model matematyczny rozwiązywanego problemu (zazwyczaj jest on podstawą do opracowania programu obliczeniowego).

4. Schemat blokowy będący graficzną prezentacją algorytmu, w postaci bloków operacyjnych lub linii ilustrujących przepływ sterowania

Najczęstszym zastosowaniem algorytmu jest tworzenie wszelkiego rodzaju instrukcji użytkowania lub obsługi urządzeń. Równie istotnym zastosowaniem algorytmu jest przygotowanie, jako schematy blokowe, do tworzenia oprogramowania komputerowego. Poza tym algorytmy mogą być używane do rozwiązywania - przez uporządkowany, logiczny zapis etapów i warunków - różnych problemów decyzyjnych.

Układanie algorytmu następuje zazwyczaj na drodze od ogółu do szczegółu i przechodzi trzy etapy:

1. Powstaje ogólny algorytm lub schemat ideowy - słowny zapis procesu.

2. Powstaje algorytm logiczny - jako rozwinięcie algorytmu ogólnego poprzez oprzyrządowanie funkcjami decyzyjnymi.

3. Powstaje algorytm logiczno - matematyczny, który umożliwia już wykonywanie obliczeń, a tym samym programowanie.

Zasady stosowane przy tworzeniu algorytmów, w szczególności schematu blokowego procesu:

1. Tworzenie algorytmu polega na takim rozłożeniu zadanego problemu na elementy, że każdy czynnik mający wpływ na rozwiązanie zostanie wyodrębniony jako osobne pytanie, na które można odpowiedzieć TAK lub NIE.

2. Logiczną współzależność układa się w ciąg stanowiący zamkniętą całość. Nazywa się go właśnie algorytmem, przy czym strzałki na jego schemacie wskazują drogę działania.

3. Algorytm można ułożyć wyłącznie wtedy, gdy w wyniku analizy procesu decyzyjnego wyodrębni się kompletny łańcuch pytań prowadzących do precyzyjnie określonych wyników.

Wskazówki techniczne przydatne przy tworzeniu algorytmu:

1. Unikać zbędnego przecinania się linii.

2. Ogólny kierunek śledzenia algorytmu powinien być z góry w dół.

3. Rozbudowa algorytmu w poziomie powinna odbywać się od strony lewej do prawej.

4. Pytania i instrukcje powinny być w osobnych kratkach.

5. Linie łączące kratki kończyć strzałkami. Stanowią one znaki potwierdzające kierunek śledzenia kroków w algorytmie.

6. Ustalić kratki jednolite dla całego algorytmu (oznaczenia stosowane w algorytmach - rys. 1)

Rys. 1. Oznaczenia stosowane w algorytmach wg PN-72/E-01226 „Przetwarzanie danych. Symbole graficzne”.

Przykłady podstawowych operacji w algorytmach przedstawiono na rysunku 2 (decyzja) oraz rysunku 3 (pętla). Z kolei przykład algorytmu dla zadania matematycznego - obliczenie pierwiastków równania kwadratowego przedstawiono na rysunku 4.

Przykład

Podajmy jeszcze jako prosty przykład algorytm obliczania pierwiastków równania kwadratowego. Równanie kwadratowe ax² + bx + c = 0 jest określone, jeśli dane są wartości współczynników a, b, oraz c (w szczególności jeżeli a ≠ 0). Rozwiązanie zadania sprowadza się wówczas do wyznaczenia pierwiastków powyższego równania (algorytm ogólny), które w zależności od (elementy logiczne) dają dwa, jedno lub brak rozwiązań w zakresie rzeczywistym (elementy matematyczne).

Na rysunku rys. 4 przedstawiono schemat blokowy ilustrujący algorytm rozwiązywania równania kwadratowego.

Rys. 4. Algorytm obliczania pierwiastków równania kwadratowego

Zadania do wykonania

należy znaleźć algorytm dla następującego problemu:

.................................................................................................................................................................

.................................................................................................................................................................

Algorytm ogólny:

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Algorytm Logiczny:

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Schemat blokowy:

Optymalizacja

a

Projektowanie

Wprowadzenie do ćwiczeń od 6 do 9

Z zagadnieniem optymalizacji mamy do czynienia, gdy stajemy wobec problemu, który może dać wiele rozwiązań (minimum dwa). Poszukujemy wówczas, takich wartości parametrów bądź czynników projektowych, które zapewniają uzyskanie minimalnej lub maksymalnej wartości wybranej cechy rozwiązania projektowego, przy równoczesnym spełnieniu wszystkich warunków ograniczających nałożonych na rozwiązanie projektowe.

Celem ćwiczenia jest przypomnienie podstawowych wiadomości z zakresu rozwiązywania problemów optymalizacyjnych. W szczególności omówione zostaną następujące zagadnienia: wskazanie funkcji celu dla analizowanego zadania, budowa modelu optymalizacyjnego, zdefiniowanie ograniczeń wpływających na uzyskanie rozwiązania oraz weryfikacja otrzymanego wyniku.

Podstawowe pojęcia i definicje

• optymalizacja - działalność której celem jest uzyskanie najlepszego rezultatu w danych warunkach i przy określonych kryteriach oceny; najlepszy rezultat będziemy nazywali optymalnym,

• funkcja celu - ściśle określony punkt widzenia problemu, inaczej mówiąc jest to kryterium w oparciu o które dokonujemy optymalizacji,

• zmienne decyzyjne - wielkości, o których możemy decydować,

• ograniczenia - ustalenie zakresu zmienności optymalizowanych parametrów,

• model optymalizacyjny - reprezentacja badanego procesu w postaci sformalizowanej - matematycznej, graficznej.

Przykłady

Projektujemy stację pompowania wody. Do dyspozycji mamy oferty kilku różnych producentów. Naszym zadaniem jest przeanalizowanie parametrów technicznych oraz ekonomicznych które umożliwiły by najlepszą pracę układu pod względem wydajności, kosztu pracy, itd.

Innym przykładem może tutaj być problem doboru silnika do projektowanego samochodu. Do dyspozycji mamy dwie alternatywy: pierwszą jest skonstruowanie silnika dokładnie pod nasze wymagania, w drugiej zaś zakładamy, iż nie będziemy konstruować nowego napędu, a jedynie skorzystamy z istniejących rozwiązań własnych lub też oferty różnych producentów. W obu przypadkach musimy jednak wziąć pod uwagę czynniki takie jak: gabaryty silnika, potrzebną moc, możliwość współpracy z projektowanymi elementami wyposażenia pojazdu, koszt zakupu (produkcji) i instalacji, itd. Przeanalizowanie tych czynników może w efekcie końcowym dać nam zbiór rozwiązań, bądź też jedno końcowe rozwiązanie zaspokajające naszą potrzebę.

Przebieg analizy optymalizacyjnej:

Należy zauważyć, iż proces optymalizacji jest silnie sformalizowany oraz powtarzalny. Umożliwia to, dla konkretnych problemów, budowanie modeli optymalizacyjnych na komputerach, a co za tym idzie obniża koszty całego przedsięwzięcia oraz ułatwia przeanalizowanie wielu wariantów w krótkim okresie czasu. Sam proces optymalizacji przebiega zwykle według następującego schematu:

1. Sformułowanie zadania optymalizacyjnego. To pierwszy etap procesu. Jest jego najważniejszą częścią, gdyż od przyjętych na tym etapie założeń dotyczących opisu problemu, zależy realizacja całego procesu. Określamy tutaj jaki parametr jest w naszym przypadku funkcją celu, to jest tą wielkością względem której dokonujemy analizy.

2. Budowa modelu matematycznego. Od poprawności zbudowanego na tym etapie modelu zależy, czy uzyskane wyniki będą poprawne. Istotne jest tutaj zachowanie proporcji pomiędzy dokładnością odwzorowania zjawiska, a szeroko rozumianymi kosztami jego budowy. Dokonujemy tutaj również określenia jakie czynniki w jaki sposób ograniczają model, powodując zawężenie obszaru poszukiwania rozwiązania optymalnego.

3. Wybór metody matematycznej rozwiązania modelu. Kolejna część procesu, polegająca na wskazaniu metody, która pozwoli na rozwiązanie problemu. Należy podjąć decyzję, czy skorzystamy z istniejących już rozwiązań, czy też należy opracować zupełnie nową metodę (metodami rozwiązywania problemów optymalizacyjnych zajmują się badania operacyjne).

4. Rozwiązanie modelu. Najbardziej oczywista część procesu optymalizacji. Polega na tradycyjnym (papier i długopis) lub też wspomaganym komputerowo (obecnie coraz powszechniejszym) rozwiązaniu zadania.

5. Weryfikacja uzyskanego rozwiązania. Badamy, czy wskazane w trakcie analizy operacyjnej rozwiązanie jest poprawne z formalnego punktu widzenia. Ponadto należy rozważyć, czy nie jest niezbędne poszerzenie zbioru dopuszczalnych rozwiązań o wartości w zakresie <+ε,-ε> lub <+x %, -x %>.

Ćwiczenie nr 6

Analiza matematyczna

Cel ćwiczenia

Przedstawienie związku pomiędzy optymalizacją a projektowaniem, a także przypomnienie podstawowych wiadomości z zakresu badań operacyjnych, to jest: poszukiwania funkcji celu dla analizowanego zadania, rozwiązania w oparciu o przyjęte ograniczenia, konstruowania modelu optymalizacyjnego.

Przykład

Określić wymiary puszki na olej o pojemności 1 litra, tak by ilość zużytego materiału była najmniejsza. Możemy wykonać puszkę w formie walca.

Sformułowanie zadania optymalizacyjnego.

Funkcją celu dla naszego zadania jest powierzchnia puszki na olej, przy czym będziemy dążyć do uzyskania odpowiedzi na pytanie: przy jakich parametrach możemy uzyskać minimalną powierzchnię tej puszki ?

Zmienne decyzyjne naszego zadania to: wymiary puszki r - promień podstawy i h - wysokość walca.

Budowa modelu matematycznego.

Modelem optymalizacyjnym naszego zadania jest równanie opisujące powierzchnię walca:

F=2πr(r+h) (6.1).

Znając objętość walca V = πr²h oraz podstawiając za V objętość zbiornika wynoszącą 1 litr mamy:

1=πr²h (6.2),

oraz:

(6.3).

Podstawiając z kolei (6.3) do wzoru na powierzchnię walca (6.1) otrzymujemy ten wzór w postaci:

F=2πr
(6.4),

co daje następnie:

F=2πr ²
(6.5).

Ostatecznie formuła określająca wielkość powierzchni puszki w zależności od promienia podstawy przyjmuje postać:

F = 2Πr² +
(6.6).

Wybór metody rozwiązania modelu.

Najprostszym sposobem znalezienia optymalnej wielkości puszki, w naszym przypadku, jest wskazanie w oparciu o analizę matematyczną - analizę pochodnej funkcji - ekstremum funkcji (6.6). Mamy więc:

F' = 4Πr -
(6.7)

Chcąc zbadać czy dana funkcja posiada ekstremum (minimum lub maksimum) analizujemy pierwszą pochodną naszej funkcji (przyrównujemy ją do zera). Ma ona następującą postać:

0 = 4Πr -
(6.8)

Otrzymujemy wówczas:

(6.9)

Analizując otoczenie miejsca zerowego pochodnej otrzymujemy:

F (r)	F (r)	F (r)
F' ⇒ ↓	F'=0	F' ⇒ ↑

Oznacza to, iż w „r” funkcja posiada ekstremum - minimum, będące poszukiwaną wielkością.

Podstawiając „r” do wzoru na wysokość puszki - „h” (6.3) otrzymujemy:

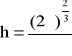
(6.10)

a więc wymiary puszki o minimalnej powierzchni wynoszą:

(6.11)

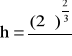
(12)

natomiast powierzchnia puszki wynosi:

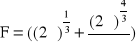
(6.13)

co jest szukaną minimalną powierzchnią puszki.

Weryfikacja uzyskanego rozwiązania.

Weryfikowanie uzyskanych rezultatów jest niezbędnym składnikiem procesu optymalizacyjnego. Otóż okazuje się, iż niektóre rozwiązania otrzymane w wyniku procesu nie spełniają naszych oczekiwań, np. w przypadku gdyby analizowana przez nas wcześniej funkcja w ekstremum nie posiadała minimum a maksimum. Wówczas wartościami spełniającymi nasze kryterium (minimalizacja powierzchni puszki) byłyby krańce analizowane przedziału zmienności funkcji.

W naszym przypadku weryfikacja zadania polega na wykonaniu wykresu ilustrującego przebieg funkcji, co zostało przedstawione poniżej, co ilustruje poniższy rysunek:

Rys. 5. Przebieg funkcji F(r) dla rozpatrywanego przypadku

Rys. 6. Przebieg funkcji F(r) w przypadku gdy r_extr ≠ r_opt

W przypadku gdyby wykres przybrał postać jak przedstawiono na rysunku 2 wówczas oznaczałoby to, iż szukane poszukiwane rozwiązanie znajdowało by się na krańcach przedziału.

Zadania do wykonania

Zadanie 1

Określić wymiary puszki na olej o pojemności 1 litra, tak by ilość zużytego materiału była najmniejsza. Puszka jest prostopadłościanem o podstawie kwadratu. Analizowana puszka jest alternatywą dla rozpatrywanej wcześniej puszki o kształcie walca - należy stwierdzić, które z rozwiązań jest dla nas korzystniejsze.

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

Zadanie 2

Poniższe zadanie jest rozwinięciem wcześniej omawianych problemów.

Przedsiębiorstwo „Opakowania na życzenie” otrzymało zamówienie na 50 000 opakowań o pojemności 1 litr. Odbiorcy jest obojętne jakiego kształtu są opakowania (walec czy prostopadłościan), natomiast zażyczył sobie, aby całość zamówionego towaru dostarczyć do jego siedziby. Firma podjęła się realizacji zamówienia i wynajęła ciężarówkę mogącą przewozić 8 kontenerów o wymiarach 1,25 x 0,9 x 1,1 m.(a x b x h) i zgodziła się na opłatę w wysokości 3,15 zł/km. Odległość od producenta opakowań do odbiorcy wynosi 370 km. Wskazać które z rozwiązań - walec czy prostopadłościan, jest dla producenta korzystniejsze (koszt materiału wynosi 8.30 zł/m²). Należy również wziąć pod uwagę, iż puszki w kształcie walca mogą zostać załadowane do kontenera na trzy sposoby:

1. denko puszki jest równoległe do dna kontenera,

2. denko puszki jest równoległe do ścianki kontenera o podstawie „a”,

3. denko puszki jest równoległe do ścianki kontenera o podstawie „b”.

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

Ćwiczenie nr 7

Systematyczne przeszukiwanie

Cel laboratorium:

Optymalizacja problemu projektowego metodą systematycznego przeszukiwania. Utrwalenie wiadomości z zakresu poszukiwania funkcji celu dla analizowanego zadania oraz rozwiązania w oparciu o przyjęte ograniczenia.

Wprowadzenie

Problemem z którym często może mieć do czynienia osoba rozwiązująca zadania projektowe jest lokalizacja obiektu(ów) w ustalonym otoczeniu (środowisku) np. lokalizacja hurtowni przy drodze, lokalizacja szybów kopalni, położenie obiektów w istniejącej hali, itp. Pomocą w rozwiązaniu tego zadania jest zbudowanie modelu - modelu alokacyjnego - który pomaga podejmować decyzje co do podziału i rozmieszczenia określonych środków pomiędzy różne cele, tak aby zoptymalizować dany system. Sprowadza się do przeanalizowania środowiska w którym ma być zlokalizowany obiekt i wyznaczenia miejsc, które spełniają nasze przyjęte założenia, czemu z powodzeniem służą metody programowania liniowego, nieliniowego, w liczbach całkowitych czy też metoda programowania dynamicznego (najbardziej znane modele alokacyjne to model transportowy, model przydziałów czy też model komiwojażera).

Poniższe ćwiczenie przybliża powyższe zagadnienie, wskazując sposób rozwiązania problemu alokacyjnego metodą systematycznego przeszukiwania zbioru, dla prostego problemu alokacji obiektu (ów) w ograniczonej przestrzeni istniejącego obiektu.

Przykład

Wskazać miejsce lokalizacji magazynu materiałów oraz półproduktów w hali produkcyjnej z działającą linią technologiczną składającą się z pięciu stanowisk o zróżnicowanej wielkości.

Aby rozwiązać powyższe zadanie należy po pierwsze sformułować jaki problem projektowy mamy rozwiązać. W naszym przypadku jest nim lokalizacja magazynu materiałów oraz półproduktów w istniejącym środowisku - hali z funkcjonującym ciągiem technologicznym.

Kolejny krok to zdefiniowanie funkcji celu. Funkcją celu w naszym przypadku jest taka lokalizacja magazynu, aby suma dróg z magazynu do punktów odbioru materiałów i półproduktów była najmniejsza.

Realizacja zadania wymaga przyjęcia następujących ograniczeń:

1. Trasa dostarczania materiałów może być prowadzona jedynie liniami prostymi przecinającymi się pod kątem prostym,

2. Trasa dostarczania materiałów nie może być zbieżna z trasą ciągu technologicznego (rys. 7),

3. Trasa dostarczania materiałów może przecinać się z trasą ciągu technologicznego jedynie pod kątem prostym,

4. Wokół magazynu powinna być wolna "strefa transportowa",

5. Wydawanie materiałów z magazynu odbywa się w jednym z jego rogów,

6. Magazyn może przylegać swoją ścianą bądź ścianami do murów magazynu.

Ze względu na opisane wyżej ograniczenia rozwiązanie problemu optymalizacyjnego sprowadza się do:

1. Wyznaczenie lokalizacji magazynu - określenia miejsc, w których magazyn jest możliwy do umiejscowienia - miejsca A, B, C.

2. Określenia odległości pomiędzy punktem wydawania materiałów, a punktami odbioru materiałów w poszczególnych stanowiskach. Droga transportu może być linią prostą, skośną lub łamaną.

3. Wpisania odległości do tablicy.

4. Obliczenia sumy dróg dla poszczególnych lokalizacji (tablica - ostatnia kolumna).

5. Wskazanie lokalizacji magazynu poprzez wskazanie rejonu o najmniejszej odległości pomiędzy magazynem a punktami odbioru.

Rys 7. Przykład lokalizacji magazynu w hali produkcyjnej

Zadanie do wykonania

Zadanie 1

Proponowane miejsca lokalizacji magazynu:

1)....................................................................................
2)....................................................................................
3)....................................................................................
4)....................................................................................

Funkcja celu: ..........................................................................................................................................

Ograniczenia modelu: ...............................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................

Model optymalizacyjny:............................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................

Długości dróg magazyn - punkty odbioru materiałów na stanowiskach

Lokalizacja Magazynu	Pkt. A	Pkt. B	Pkt. C	Pkt. D	Pkt. E	Pkt. F	Pkt. G	Pkt. H	Suma
1
2
3
4
5
6
7

Rozwiązanie

Lokalizacją o najniższej sumie dróg jest lokalizacja nr ............, o łącznej długości dróg wynoszącej ....................... jednostek

Zadanie 2

Do rozwiązania jest następujące rozwinięcie poprzedniego problemu: czy powinniśmy zbudować jeden magazyn o powierzchni 24 m2, czy też dwa lub trzy mniejsze ? Okres funkcjonowania magazynu(ów) wynosi 5 lat. Koszt budowy magazynu wynosi 200 zł/m2 oraz dodatkowo 800 zł za każdy magazyn. koszt użytkowania magazynu(ów) wynosi 2 zł/m2/mies., koszt transportu materiałów do punktów odbioru: 2 gr/m, dostawa materiałów 2/zmianę (2 zmiany robocze na dniówkę).

Rozwiązanie zadania 2 jest zbliżone do zadania 1. W pierwszej części dokonujemy lokalizacji magazynów o różnych powierzchniach w planie hali produkcyjnej, a następnie określamy długości dróg z magazynów do punktów odbioru. kolejnym krokiem jest określenie funkcji celu, budowa modelu optymalizacyjnego oraz rozwiązanie go.

Funkcją celu umożliwiającą rozwiązanie problemu jest minimalizacja kosztów funkcjonowania układu: magazyn(y) - transport części.

min - K(budowa - kb, utrzymanie - ku, transport -kt)

Zmiennymi decyzyjnymi są:

1. Ilość oraz powierzchnia magazynów,

2. Długość dróg transportu.

Model matematyczny naszego zadania jest następujący:

K = kb + ku + kt

gdzie:

koszt budowy: kb = (koszt stały budowy magazynu (800 zł) * ilość budowanych magazynów) + koszt powierzchni magazynu (24 m2 * 200 zł/m2)

koszt użytkowania: ku = ilość czasu przez jaką będą użytkowane magazyny (5 lat * 12 miesięcy) * koszt utrzymania 1 m2 magazynu ( 2 zł/m2)

koszt transportu: kt = suma dróg w danym wariancie * koszt transportu na odcinku drogi (2 gr/m) * ilość kursów na zmianę (2 kursy) * liczba zmian w dniu (2 zmiany) * liczba dni roboczych w roku (250 dni) * liczba lat (5 lat)

Wariant	Koszt budowy Kb	Koszt utrzymana Ku	Koszt transportu Kt	Suma kosztu ΣK
1 magazyn - a
- b
- c
2 magazyn - a
- b
- c
3 magazyn - a
- b
- c

Rozwiązanie.

Rozwiązaniem o najniższym koszcie funkcjonowania układu magazyn(y) punkty odbioru jest wariant .......... w którym przyjęto, iż zostaną zbudowane ........ magazyny

Ćwiczenie nr 8

Programowanie dynamiczne

Cel laboratorium:

Optymalizacja problemu projektowego metodą programowania dynamicznego. Utrwalenie wiadomości z zakresu poszukiwania funkcji celu dla analizowanego zadania oraz rozwiązania w oparciu o przyjęte ograniczenia.

Wprowadzenie

Programowanie dynamiczne jest jedną z technik matematycznych, którą można zastosować do rozwiązywania takich problemów, jak: zagadnienia dyliżansu, zagadnienia finansowania inwestycji, optymalizacja zapasów, alokacja zasobów, czy wymiana majątku trwałego. Warto przy tym podkreślić, że programowanie dynamiczne należy traktować bardziej jako sposób podejścia do rozwiązywania problemu niż jako pojedynczy uniwersalny algorytm. W dalszej części ograniczono się do bliższego scharakteryzowania zagadnienia finansowania inwestycji oraz zagadnienia wyboru trasy.

Zagadnienie finansowania przedsięwzięcia inwestycyjnego można scharakteryzować jako problem alokacji określonego zasobu środków (w tym przypadku wyrażonego w jednostkach pieniężnych) pomiędzy poszczególne zadania (programy inwestycyjne), tak aby osiągnąć maksymalny efekt. Przyjmuje się przy tym następujące założenia:

1. Efekt zastosowania każdego z programów inwestycyjnych nie zależy od tego, czy zostały zastosowane równocześnie inne programy inwestycyjne.

2. Zwrot nakładów inwestycyjnych jest mierzony w tych samych jednostkach.

3. Nakłady inwestycyjne są liczbami całkowitymi.

4. Funkcje określające związki między nakładami inwestycyjnymi a wysokością zwrotu nakładów są niemalejące.

Nieco inny problem niesie ze sobą tzw. zagadnienie dyliżansu, polegające na poszukiwaniu optymalnej drogi w sieci. Nazwa zagadnienia pochodzi od pewnego kupca amerykańskiego, który transportował towary ze Wschodniego Wybrzeża USA na Wybrzeże Zachodnie, używając w tym celu różnych połączeń realizowanych za pomocą dyliżansu. Oczywiście, chodziło o dobór takich połączeń, aby transport odbywał się w miarę bezpiecznie, a miarą bezpieczeństwa na danej linii były stawki pobierane przez towarzystwo ubezpieczeniowe. Rozwiązanie problemu wymagało podzielenia całej trasy na etapy, a w każdym z etapów określenia miast etapowych oraz wszystkich możliwych połączeń pomiędzy nimi.

Łatwo można sobie wyobrazić inne możliwości zastosowania tak sformułowanego zagadnienia do szerokiej klasy problemów poszukiwania najkrótszej lub najdłuższej drogi w sieci (internet - wybór trasy, rozdział środków inwestycyjnych, rozdział zadań produkcyjnych).

Oba wcześniej wymienione zagadnienia można rozwiązać stosując podejście charakterystyczne dla programowania dynamicznego. Polega ono na podziale zagadnienia pierwotnego na podproblemy lub etapy, a następnie na ich sekwencyjnym rozwiązywaniu, aż do znalezienia rozwiązania optymalnego. Stosuje się przy tym, niezależnie od algorytmu, zasadę optymalności Bellmana, w myśl której optymalne rozwiązanie zagadnień zakresu programowania dynamicznego ma tę własność, że optymalne rozwiązanie dla k-tego etapu jest jednocześnie rozwiązaniem optymalnym dla etapów k+1,..., N. Tak więc optymalne rozwiązanie dla etapu pierwszego stanowi optymalne rozwiązanie dla całego problemu.

W związku z powyższą zasadą problem z zakresu programowania dynamicznego rozwiązuje się rozpoczynając od poszukiwania rozwiązania dla ostatniego etapu (N), a następnie cofając się poszukuje się rozwiązania dla etapu N-1. Uzyskane w ten sposób rozwiązanie dla etapów N-1 oraz N jest optymalne bez względu na to, w jaki sposób osiągnięto etap N-1. Powtarzając w powyższy sposób etap po etapie, dochodzimy do rozwiązania optymalnego dla pierwszego etapu, a więc i dla całego problemu.

Powyższa zasada zostanie zilustrowana na przykładzie zagadnienia alokacji środków inwestycyjnych.

Przykład

Przedsiębiorca Jerzy Płatek, posiadający kredyt inwestycyjny w wysokości 6 mln zł oraz halę produkcyjną w Krakowie, postanowił zainstalować nowoczesne linie piekarnicze: francuską (F), szwedzką (S) oraz polską (P). Dobowe zdolności produkcyjne linii (w tonach wyprodukowanego pieczywa), w zależności od wysokości nakładów inwestycyjnych przeznaczonych na zainstalowanie linii produkcyjnej danego typu, przedstawiono w tablicy 1.

Tablica 1

Nakłady (w mln zł)			0		1		2		3		4		5		6
Zdolności produkcyjne linii (w t/d)	F		0		6		12		12		12		15		20
		S		0		5		8		11		14		17		18
		P		0		4		15		15		15		15		16

Analiza rynku wykazała, że każda z linii produkcyjnych pozwala uzyskiwać jednakowe zyski w przeliczeniu na 1 t pieczywa. Jerzy Płatek musi więc w tym przypadku podjąć decyzję dotyczącą podziału kredytu pomiędzy poszczególne programy inwestycyjne, tak aby piekarnia osiągnęła maksymalną, dobową zdolność produkcyjną.

UWAGA: Następuje tutaj pierwszy element analizy optymalizacyjnej - wskazana zostaje funkcja celu oraz ograniczenia.

Funkcją celu jest więc taki rozdział środków inwestycyjnych, aby efekt w postaci wielkości produkcji był maksymalny:

ΣZ_p(N_i) ⇒ max, (8.1)

gdzie: Z_p - zdolności produkcyjne,

N_i - nakłady inwestycyjne.

Model matematyczny problemu sprowadza się zatem do prostej sumy zdolności produkcyjnych z trzech linii w zależności od posiadanych środków inwestycyjnych i przyjmuje postać:

Z_p = Z_p1(N₁) + Z_p2(N₂) + Z_p3(N₃) (8.2)

Rozwiązanie

Powyższy problem, należący do kategorii programowania dynamicznego, można rozwiązać za pomocą procedury opisanej w kilku etapach.

Krok 1

Załóżmy, że jedynym możliwym rozwiązaniem jest zakupienie polskiej linii produkcyjnej i zadajmy sobie pytanie dotyczące uzyskanej w ten sposób dobowej zdolności produkcyjnej w zależności od zainwestowanej kwoty. Wyniki pokazano w tablicy 2.

Tablica 2

Nakłady [mln zł]	0	1	2	3	4	5	6
Zdolności produkcyjne linii P [t]	0	4	15	15	15	15	16

W tym przypadku jedynym sensownym rozwiązaniem jest zainwestowanie 6 mln zł w polską linię produkcyjną w celu osiągnięcia zdolności produkcyjnej 16 t pieczywa na dobę. Rezultat ten zapiszemy następująco:

P(6) = 16

co oznacza, że 6 mln zł zainwestowane w polską linię produkcyjną zapewnia produkcję 16 t pieczywa na dobę. (Ponieważ niezależnie od poziomu produkcji mamy jednakowy zysk jednostkowy, więc maksymalizacja produkcji dawać nam będzie maksymalizację zysku).

Krok 2

Załóżmy, że dostępne są dwa typy linii produkcyjnych: P oraz S i zadajmy sobie następujące pytanie: jak należy podzielić kredyt inwestycyjny pomiędzy te dwa programy, aby uzyskać maksymalną dobową zdolność produkcyjną?

W tym przypadku możliwe jest siedem wariantów podziału 6 mln zł kredytu, które dają następujące dobowe zdolności produkcyjne:

P(6) + S(0) = 16 + 0 = 16,

P(5) + S(1) = 15 + 5 = 20,

P(4) + S(2) = 15 + 8 = 23,

P(3) + S(3) = 15 + 11 = 26,

P(2) + S(4) = 15 + 14 = 29,

P(1) + S(5) = 4 + 17 = 21,

P(0) + S(6) = 0 + 18 = 18.

W powyższej sytuacji należy więc zainwestować 2 mln zł w polska linię oraz 4 mln zł w szwedzką linię, osiągając w ten sposób 29 t pieczywa na dobę.

Krok 3

Spróbujmy obecnie znaleźć optymalny podział kredytu pomiędzy linię P oraz S przy malejącej kwocie nakładów inwestycyjnych:

A) 5 mln zł na linie P oraz S

P(5) + S(0) = 15 + 0 = 15,

P(4) + S(1) = 15 + 5 = 20,

P(3) + S(2) = 15 + 8 = 23,

P(2) + S(3) = 15 + 11 = 26,

P(1) + S(4) = 4 + 14 = 18,

P(0) + S(5) = 0 + 17 = 17.

W przypadku dysponowania kwotą 5 mln zł na linie P oraz S należy zainwestować 2 mln zł w linię P oraz 3 mln zł w linię S i osiągnąć 26 t pieczywa na dobę. Rezultat zapiszemy w następujący sposób:

P(2) + S(3) = 26.

B) 4 mln zł na linie P oraz S

P(4) + S(0) = 15 + 0 = 15,

P(3) + S(1) = 15 + 5 = 20,

P(2) + S(2) = 15 + 8 = 23,

P(1) + S(3) = 4 + 11 = 15,

P(0) + S(4) = 0 + 14 = 14.

W przypadku dysponowania kwotą 4 mln zł należy zainwestować po 2 mln zł w linie P oraz S:

P(2) + S(2) = 23.

C) 3 mln zł na linie P oraz S

P(3) + S(0) = 15 + 0 = 15,

P(2) + S(1) = 15 + 5 = 20,

P(1) + S(2) = 4 + 8 = 12,

P(0) + S(3) = 0 + 11 = 11.

W tym przypadku należy zainwestować 2 mln zł w linię P i 1 mln zł w linię S:

P(2) + S(1) = 20.

D) 2 mln zł na linie P oraz S

P(2) + S(0) = 15 + 0 = 15,

P(1) + S(1) = 4 + 5 = 9,

P(0) + S(2) = 0 + 8 = 8.

W tym przypadku należy zainwestować 2 mln zł w linię polską (P):

P(2) + S(0) = 15.

E) 1 mln zł na linie P oraz S

P(1) + S(0) = 4 + 0 = 4,

P(0) + S(1) = 0 + 5 = 5.

W tym przypadku należy zainwestować 1 mln zł w linię szwedzką (S):

P(0) + S(1) = 5.

A zatem w kroku 3 określiliśmy optymalne kombinacje nakładów na linie P oraz S.

6 mln zł P(2) + S(4) = 29.

A) 5 mln zł P(2) + S(3) = 26.

B) 4 mln zł P(2) + S(2) = 23.

C) 3 mln zł P(2) + S(1) = 20.

D) 2 mln zł P(2) + S(0) = 15.

E) 1 mln zł P(0) + S(1) = 5.

Krok 4

Konsekwentnie, w kroku 4 wystarczy rozpatrzyć wszystkie kombinacje podziału 6 mln zł kredytu pomiędzy linię F oraz linię P + S. Zdolności produkcyjne w zależności od nakładów kredytowych przedstawiono w tablicy 3.

Tablica 3

Krok	0	1	2	3	4	5	6
F (z tablicy 1)	0	6	12	12	12	15	20
P + S (z kroków 2 i 3)	0	5	15	20	23	26	29

Jak łatwo można zauważyć, możliwych jest siedem wariantów podziału 6 mln zł kredytu pomiędzy linię F oraz linię P + S, dających następujące zdolności produkcyjne:

F(6) + (S + P)(0) = 20 + 0 = 20,

F(5) + (S + P)(1) = 15 + 5 = 20,

F(4) + (S + P)(2) = 12 + 15 = 27,

F(3) + (S + P)(3) = 12 + 20 = 32,

F(2) + (S + P)(4) = 12 + 23 = 35,

F(1) + (S + P)(5) = 6 + 26 = 32,

F(0) + (S + P)(6) = 0 + 29 = 29.

Tak więc maksymalną zdolność produkcyjną piekarni można uzyskać inwestując 2 mln zł w linię francuską F oraz 4 mln zł w linię S i P. Aby uzyskać rozwiązanie ostateczne, wystarczy odszukać w kroku 3 optymalny sposób podziału tych 4 mln zł pomiędzy linie S oraz P. W rezultacie otrzymujemy rozwiązanie: 2 mln zł na linię F, 2 mln zł na linię P oraz 2 mln zł na linię S, co zapewnia 35 t pieczywa na dobę.

Zadanie do wykonania

Firma „DOSKONAŁE OPROGRAMOWANIE Z REDMOND” zamierza zainwestować 8000 USD. Oszacowano, iż analizowana inwestycja może przynieść zwrot w wysokości:

G₁ = x + 500,

G₂ = 1000 * 80
,

G₃ = 0,015 *
;

przy czym wynik końcowy jest kombinacją trzech wariantów, a „x” oznacza nakłady inwestycyjne (w uproszczeniu podane z dokładnością do 1000 USD)

Wybrać optymalny wariant realizacji inwestycji, tak aby nakłady przyniosły maksymalną korzyść.

Rozwiązanie zadania:

1. Uzyskane efekty

	0	1000	2000	3000	4000	5000	6000	7000	8000
G1
G2
G3

2. Analiza optymalizacyjna:

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

................................................................................................................................................................

Ćwiczenie nr 9:

Programowanie sieciowe

Cel laboratorium:

Optymalizacja problemu projektowego metodą sieciową CPM - COST. Utrwalenie wiadomości z zakresu poszukiwania funkcji celu dla analizowanego zadania oraz rozwiązania w oparciu o przyjęte ograniczenia.

Wprowadzenie

W trakcie procesu projektowania często mamy do czynienia z sytuacją, gdy konieczna jest jednoczesna realizacja wielu czynności. Ich zgranie, w sposób umożliwiający najefektywniejsze wykorzystanie posiadanych zasobów, jest często problemem od rozwiązania którego zależy wykonanie całości zadania. Analiza siatek czynności (CPM - Critical Patch Method) jest jedną z metod umożliwiających przede wszystkim ustalenie powiązań pomiędzy poszczególnymi czynnościami analizowanego procesu, badanie czynności występujących na drodze krytycznej, wykazywanie zapasu czasów itd., zaś metoda CPM-COST umożliwia dodatkowo badanie na powiązanie analizy czasowej danego zadania z jej aspektami ekonomicznymi.

Optymalizacja przedsięwzięcia metodą CPM składa się z kilku etapów i polega na:

1. wyodrębnieniu i zestawieniu wchodzących w jego skład czynności (zadań cząstkowych),

2. ocenie parametrów poszczególnych czynności i zdarzeń (czasu, nakładów, zasobów),

3. konstrukcji sieci zależności technologicznych,

4. wyznaczeniu podstawowych charakterystyk sieci, dotyczących zarówno poszczególnych czynności i zdarzeń, jak też całego projektu,

5. wyznaczeniu tzw. ścieżki krytycznej.

Przy czym:

• pod pojęciem przedsięwzięcia rozumiemy zorganizowane działanie zmierzające do osiągnięcia wyznaczonego celu, zawarte w skończonym przedziale czasu oraz realizowane przez skończoną wielkość zasobów (środki finansowe, zasoby ludzkie, środki techniczne),

• 
  pod pojęciem zdarzenia rozumiemy moment rozpoczęcia lub też zakończenia czynności (przedstawiany zwykle w postaci koła lub innej figury geometrycznej),

• 
  czynnością nazywać będziemy dowolną wyodrębnioną część przedsięwzięcia, która charakteryzuje się czasem trwania oraz zużywaniem środków, a przedstawiana jest w postaci wektora,

• czynnością pozorną nazwiemy taką czynność której czas realizacji oraz wykorzystanie środków jest zerowe, a czynność ta służy jedynie do przedstawienia zależności pomiędzy następowaniem czynności,

• drogą albo ścieżką w sieci nazywamy ciąg czynności oraz zdarzeń umożliwiający przejście od początku do końca sieci. W przypadku drogi o najdłuższym czasie przejścia mówimy o drodze krytycznej, a jej zapas czasu wynosi zero.

Wyznaczenie drogi krytycznej umożliwia kontrolę całego procesu, a co za tym idzie kontrolę dotrzymania terminu końcowego.

Przykład

Realizujemy proces projektowania budynku mieszkalnego obejmującego następujące czynności składające się na całe przedsięwzięcie:

Tablica 4

Czynność	Czynności poprzedzające	Czas nominalny realizacji czynności tn	Czas graniczny realizacji czynności tgr	Koszt nominalny realizacji czynności Kn	Koszt graniczny realizacji czynności Kgr
A	-	20	15	3500	6000
B	-	10	5	1000	1500
C	A	5	3	2000	2500
D	A	6	3	2000	3000
E	B	14	9	7000	10000
F	C, D	3	3	1000	1000

przy czym:

• pod pojęciem normalnego czasu trwania - t_n - czynności rozumiemy czas któremu odpowiadają najniższe koszty wykonania K_n,

• czas graniczny - t_g -, to najkrótszy możliwy ze względów technicznych i technologicznych czas wykonania czynności przy koszcie granicznym K_g

Model sieciowy takiego przedsięwzięcia wygląda jak przedstawiono na rysunku poniżej. Tworzenie takiego modelu podlega następującym regułom:

Rys 8. Model sieciowy przedsięwzięcia

1. istnieje dokładnie jeden wierzchołek (zdarzenie) początkowy i jeden wierzchołek końcowy (postulat ten można spełnić wprowadzając czynności pozorne),

2. wierzchołki wektorów są uporządkowane , tzn. każdy poprzednik ma mieć numer mniejszy lub wcześniejszą literę od następnika (co uniemożliwia wprowadzenie ścieżek cyklicznych lub pętli),

3. dwa zdarzenia są połączone tylko jedną czynnością; jeżeli kilka czynności poprzedza jedno zdarzenie, wówczas należy wprowadzić czynności pozorne,

4. każda czynność może być zrealizowana tylko jeden raz z prawdopodobieństwem równym jeden podczas wykonywania przedsięwzięcia.

Jego uzupełnieniem jest opis ilościowy przedsięwzięcia charakteryzujący czasy trwania poszczególnych czynności. W charakterystykach tych opisuje się następujące wielkości:

i - numer kolejnego zadania,

t - najwcześniejszy możliwy moment zaistnienia zdarzenia,

T - najpóźniejszy dopuszczalny moment zaistnienia zdarzenia,

L - zapas czasu.

Przedstawiane zwykle w postaci:

Analizę rozpoczynamy od określenia najwcześniejszego możliwego momentu zaistnienia zdarzenia t_i (wypełniamy lewą ćwiartkę). Przyjmujemy, iż najwcześniejszy moment rozpoczęcia zdarzenia 1 jest równy zero (t_i = 0).Z kolei najwcześniejszy moment zaistnienia następnego zdarzenia „j” jest równy sumie najwcześniejszego zdarzenia oraz czasu trwania czynności prowadzącej od zdarzenia „i” do zdarzenia „j”. A więc w naszym przypadku:

t₂ = t₁ +t_a = 0 + 20 = 20;

t₃ = t₁ +t_b = 0 + 10 = 10.

Ponieważ realizacja niektórych zadań wymaga wykonania wcześniej kilku równolegle realizowanych czynności, dlatego najwcześniejszym możliwym momentem zaistnienia zdarzenia t_n jest taka wielkość która spełnia następującą zależność:

(9.1)

czyli:

t₅ = max{20+5; 20+6} = 26.

Wyznaczamy w ten sposób wszystkie najwcześniejsze momenty zaistnienia zdarzeń t_i. Umożliwia to stwierdzenie, iż najwcześniejszym możliwy czas realizacji całego przedsięwzięcia wynosi 29 jednostek czasu.

Wyznaczamy teraz najpóźniejszy dopuszczalny moment zaistnienia zdarzeń. Zaczynając od ostatniego zdarzenia i poruszając się w kierunku przeciwnym do zwrotu strzałek. Przyjmujemy, iż najpóźniejszy dopuszczalny termin zaistnienia zdarzenia końcowego jest równy najwcześniejszemu możliwemu terminowi jego zaistnienia, tj. T_n = t_n. Wielkość tą wpisujemy w prawej ćwiartce symbolu ostatniego zdarzenia. Możemy teraz określić najpóźniejsze dopuszczalne terminy realizacji pozostałych zdarzeń poprzez odjęcie od najpóźniejszego dopuszczalnego terminu zdarzenia następnego (j) czasu trwania czynności i-j. W przypadku, gdy do zdarzenia dochodzą co najmniej dwie czynności wybieramy dla nich wielkość najmniejszą.

(9.2)

Na przykład:

t₅ = min{3+5; 3+6} = 8

Mając wyznaczone najpóźniejsze dopuszczalne oraz najwcześniejsze możliwe terminy zaistnienia poszczególnych zdarzeń (T ora t) określamy zapas czasu jakim dysponujemy dla poszczególnych zdarzeń:

L_j = T _j - t _j. (9.3)

W przypadku, gdy zapas czasu dla czynności jest równy zeru (L_j = 0), wówczas mamy do czynienia z czynnością krytyczną. Wyznaczenie wszystkich zdarzeń krytycznych umożliwia z kolei znalezienie ścieżki krytycznej, co daje mam możliwość planowania, koordynacji oraz kierowania całym procesem w taki sposób, aby nie nastąpiło opóźnienie w realizacji całego zadania.

Równie istotnym co ilościowe, jest ekonomiczne ujęcie metody CPM. Jego realizacja umożliwia kompresję sieci, a co za tym idzie skrócenie okresu realizacji przedsięwzięcia, co ma duże znaczenie dla ewentualnego inwestora. Należy przy tym wziąć pod uwagę, iż skrócenia czasu realizacji należy dokonać w taki sposób, aby koszty tego procesu były najniższe. Oznacza to, iż w pierwszym rzędzie przyspieszać należy te czynności w których koszt przyspieszenia ich realizacji będzie najniższy (oczywistym wydaje się przyjęcie założenia, iż przyspieszenie czynności wiąże się ze wzrostem kosztu jej realizacji).

Zakładając, iż przyrost kosztów realizacji zadania jest liniowy (w zależności od czasu realizacji zadania) możemy wyznaczyć średni gradient kosztu S:

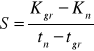
(9.4)

Współczynnik ten określa przyrost kosztów wykonania zadania wynikający z skrócenia czasu wykonania zadania o jednostkę czasu, przy czym:

• t_n - normalny czas trwania czynności, a rozumiemy przez to, czas któremu odpowiadają najniższe koszty wykonania K_n,

• t_gr - czas graniczny - najkrótszy możliwy ze względów technicznych i technologicznych czas wykonania czynności przy koszcie granicznym K_gr.

W naszym przypadku dla poszczególnych czynności współczynnik gradientu S wynosi odpowiednio:

S(a) = S(b) = S(c) = S(d) = S(e) =

500 100 250 333 500

Sam proces kompresji polega na [3]:

1. Wyznaczeniu ścieżki krytycznej.

2. Wyznaczeniu gradientu kosztów S dla czynności leżących na ścieżce krytycznej.

3. Wyeliminowaniu tych czynności dla których S=0.

4. Skróceniu czasu realizacji czynności dla czynności o S = min (<0).

5. Skróceniu czasu realizacji czynności dla kolejnych czynności (wraz z wzrostem wartości gradientu S).

Uwagi:

• skracanie czasu realizacji czynności ograniczone jest czasem granicznym t_gr danej czynności,

• może pojawić się nowa ścieżka krytyczna (w przypadku jeżeli na dotychczasowej drodze krytycznej skrócimy realizację procesu o wielkość równą co najmniej zapasowi czasu jaki mamy do dyspozycji w innych procesach składających się na całe zadanie).

Jeżeli wystąpią dwie lub więcej ścieżek krytycznych, wówczas skracanie czasu na wszystkich tych ścieżkach jest dokonywane o tą samą wielkość czasu. Gdy wszystkie czynności leżące na którejkolwiek drodze krytycznej osiągną czas graniczny wówczas uzyskujemy najkrótszy czas realizacji zadania. Całkowite koszty przyspieszenia realizacji zadania są sumą wszystkich kosztów skrócenia czasu realizacji czynności.

Poniżej przedstawiono wykres sieciowy zadania dla początkowych oraz skompresowanych czasów realizacji poszczególnych zadań (rys. 9 oraz rys. 10).

Rys 9. Wykres sieciowy zadania - wyznaczenie drogi krytycznej

Rys 10. Wykres sieciowy zadania dla skompresowanego czasu realizacji zadania.

Zadania do wykonania

Zadanie 1

Wyznaczyć drogę krytyczną dla procesu przedstawionego w tablicy poniżej, a następnie dokonać skrócenia czasu realizacji zadań. Narysować schemat sieciowy drogi krytycznej oraz schemat sieciowy dla skompresowanego czasu realizacji zadania.

Czynność	Czynności poprzedzające	tn	tgr	Kn	Kgr	S
A	-	7	4	200	300
B	-	3	2	500	800
C	-	6	2	400	800
D	A, B	9	5	1500	2500
E	A, B	8	6	800	900
F	D	5	4	500	700
G	E, C	5	5	200	200

Zadanie 2

Wyznaczyć drogę krytyczną dla procesu przedstawionego w tablicy poniżej, a następnie dokonać skrócenia czasu realizacji zadań. Narysować schemat sieciowy drogi krytycznej oraz schemat sieciowy dla skompresowanego czasu realizacji zadania.

Czynność	Czynności poprzedzające	tn	tgr	Kn	Kgr	S
A	-	3	1	800	2000
B	-	8	4	1800	3000
C	A	6	5	1100	1200
D	B	3	2	600	800
E	B	2	1	400	500
F	C, D	9	7	2200	2600
G	E	3	3	900	900

Ekonomiczna Efektywność Inwestycji a Projektowanie

Wprowadzenie do ćwiczeń od 10 do 12

Analiza projektu jest procesem, z którym spotykamy się:

• w momencie uruchomienia projektu (faza przedinwestycyjna), aby pogłębiać jego analizę i znaleźć rozwiązanie,

• okresowo, w trakcie realizacji projektu, kiedy zmiany w otaczającym środowisku i poziomie wiedzy, lub stwierdzenie poważnych rozbieżności w stosunku do tego co było przewidziane, prowadzą do zrewidowania wcześniejszej analizy.

Analizy projektu dokonywane są głównie w kategoriach ekonomicznych i poprzez rachunek jego rentowności. Dotyczyć to będzie porównania kosztów realizacji projektu i kosztów jego eksploatacji (dla całego okresu życia przyjętego jako realistyczny) z korzyściami uzyskanymi dzięki jego realizacji. Sprawia to oczywiście niekiedy pewne problemy, na przykład w sytuacji gdy musimy określić wartość niezanieczyszczania środowiska naturalnego lub poziom satysfakcji z rozwiązań administracyjnych.

Z punktu widzenia przedsiębiorcy kryterium decyzji inwestycyjnej jest zwrot zainwestowanego kapitału czyli zysk.

Tak więc analiza rentowności inwestycji opiera się przede wszystkim na określeniu stosunku między wielkością zysku i zainwestowanego kapitału. Zysk stanowi najbardziej syntetyczne podsumowanie działalności z ekonomicznego punktu widzenia, a jednocześnie kryje w sobie zachęty do dynamizowania produkcji, przyspieszenia sprzedaży poprzez skracanie cykli i do poprawy wyników ekonomicznych różnymi sposobami, w tym zwłaszcza przez racjonalne gospodarowanie.

Przy sporządzaniu rachunku należy zwrócić uwagę na porównywalność poszczególnych jego elementów, a także różnych wariantów danego projektu inwestycyjnego w zakresie:

• wzajemnej zależności nakładów i efektów;

• wpływu rozwiązań lokalizacyjnych;

• rozłożenia nakładów i efektów w czasie.

Dla sprawdzenia tego rodzaju wariantów do porównywalności, należy w rachunku uwzględnić nakłady na inwestycje towarzyszące. Konieczność uwzględnienia w rachunku zasady porównywalności wariantów z punktu widzenia rozłożenia nakładów i efektów w czasie wynika z faktu, że warianty mogą różnić się:

• długością okresu związanego z przygotowaniem i realizacją badanej inwestycji (w szczególności długością okresu budowy);

• długością okresu eksploatacji;

• rozkładem nakładów i efektów w obu tych okresach.

Jeżeli zasada poszukiwania rozwiązań alternatywnych nie jest przestrzegana w procesie opracowania projektu przedsięwzięcia inwestycyjnego, dokonany wybór może okazać się bardzo kosztowny, jeżeli - z powodów niedostatecznych prac przygotowawczych - wybrany projekt trzeba będzie odrzucić na rzecz jakiegoś rozwiązania alternatywnego.

Istnieje wiele różnorodnych kryteriów oceny rentowności projektów. Do najważniejszych z nich należą:

• okres zwrotu nakładów kapitałowych;

• wartość zaktualizowana netto NPV;

• wskaźnik wartości zaktualizowanej netto;

• wewnętrzna stopa zwrotu;

• próg rentowności inwestycji.

Przedmiotem niniejszego przewodnika nie jest ich szczegółowe i dokładne omówienie. W dalszej części przewodnika podano jedynie ogólne zasady i podstawowe wzory obliczeń wartości tych wskaźników. Niemniej jednak ważnym do odnotowania jest, że:

1. Kryteria rentowności stanowią jedynie narzędzie pomocnicze w podejmowaniu decyzji. Byłoby wielką pomyłką przydzielanie im magicznej władzy akceptacji lub odrzucenia jakiegoś projektu tylko z powodu jego pozycji w stosunku do takiego to a takiego kryterium. W rzeczywistości uzyskane rezultaty są różne w zależności od przyjętego kryterium, a obliczenia są wykonywane na bazie wielu hipotez mniej lub bardziej niepewnych (ceny surowców, ceny wyrobów finalnych, stopa dyskontowa itd...);

2. Każde kryterium ma swoje precyzyjne znaczenie wypływające ze sposobu jego wyliczenia. W zależności od rodzaju projektu, takie lub inne kryterium będzie miało większy lub mniejszy ciężar gatunkowy: w projekcie o dużym ryzyku przestarzałości kryterium okresu zwrotu nakładów kapitałowych będzie bardziej znaczące od wewnętrznej stopy zwrotu.

3. Badania czułości kryteriów rentowności na zmiany wartości hipotez bazowych są zasadniczymi dla wykrycia, które hipotezy są podstawowymi (najbardziej wpływowymi) i począwszy od jakich wartości tych hipotez rentowność projektu może być wątpliwa. Badania te, na bazie prawdopodobieństwa osiągnięcia tych wartości - kluczowych, pomagają w podjęciu decyzji o realizacji projektu.

Ćwiczenie nr 10:

Rachunek aktualizacji

Wprowadzenie

Oceniając efektywność inwestycji, dokonujemy porównań między bieżącymi nakładami inwestycyjnymi, a przyszłymi dochodami z inwestycji. Zbilansowanie i porównanie wydatków i efektów wymaga przeliczenia ich wartości na określony, dowolnie wybrany moment czasowy. Rolę narzędzia sprowadzającego nakłady i efekty w rachunku inwestycji do porównywalności czasowej pełni metoda rachunku aktualizacji. Metoda ta opiera się na analizie rachunku oprocentowania i dyskonta, za pomocą którego dokonuje się bezpośredniego powiązania wartości z czasem. U podstaw metody rachunku aktualizacji leży założenie, że wartość wydatków lub wpływów jest funkcją czasu o charakterze wykładniczym. Wielkość zmiany wartości wydatków lub wpływów w czasie, jest stymulowana przyjęciem określonej wielkości stopy procentowej. Zmiana wartości kapitału w czasie może być dokonywana w dyskretnych przedziałach czasu lub ciągle w czasie. W praktyce rachunku ekonomicznej efektywności inwestycji stosuje się rachunek aktualizacji w odmianie dyskretnej.

Podstawowe założenia dla rachunku aktualizacji w odmianie dyskretnej są następujące:

1. dyskretnym przedziałem czasu jest jeden rok.

2. stopa procentowa wynosi r procent w skali roku.

3. kwoty podlegające oprocentowaniu (wpływy lub wydatki) kumulowane są na końcu każdego roku.

4. odsetki są dopisywane do wartości wyjściowej na końcach dyskretnych przedziałów czasu.

Rachunek oprocentowania i rachunek dyskonta

Rachunek oprocentowania jest jedną z podstawowych metod służących analizie ekonomicznej efektywności projektu. Umożliwia ona porównanie różnych rozwiązań możliwych do realizacji w ramach jednego projektu. Wprowadzenie porównawczej metody wynika z faktu, iż oceniane warianty rozwiązań mogą się różnić długością okresu realizacji i eksploatacji oraz rozkładem nakładów i efektów.

Dyskontowanie jest odwrotnością oprocentowania i wyznacza aktualną wartość kapitału, która wystąpi w przyszłości.

W rachunku aktualizacji stosowane są następujące oznaczenia:

k_o - wartość początkowa kapitału zainwestowanego na oprocentowanie,

r - stopa procentowa,

O - kwota odsetek,

t - czas oprocentowania,

T -  ilość dni w roku (banki przyjmują najczęściej 365 dni),

k_n - wartość przyszła kapitału zainwestowanego na oprocentowanie,

Oprocentowanie proste

Kwota odsetek przy oprocentowaniu prostym zależy od wartości początkowej kapitału k_o, stopy procentowej r oraz czasu oprocentowania T według poniższego wzoru:

(10.1)

Przykład:

Przedsiębiorca ulokował w banku 5 maja 10 000 zł na okres 1 roku. Warunki lokaty określają, że w przypadku wcześniejszego podjęcia kwoty, zamiast stopy procentowej 15%, klientowi przysługuje roczna stopa procentowa 9%. Przedsiębiorca zmuszony był pobrać ulokowaną w banku kwotę 30 grudnia tego samego roku, wobec tego otrzymał odsetki w kwocie:

zł

Oprocentowanie proste w okresie rocznym

Oprocentowanie proste stosowane jest w praktyce w okresie krótszym niż rok, co nie oznacza, ze nie można go stosować dla okresów rocznych. W przypadku rocznego naliczania oprocentowania, przyrost kapitału początkowego k_o w kolejnych latach określimy następująco:

po pierwszym roku
(10.2)

po drugim roku
(10.3)

po n - tym roku
(10.4)

Przykład:

Ulokowana w banku kwota 10 000 zł na oprocentowanie roczne w wysokości 15% bez możliwości kapitalizacji odsetek, po pięciu latach wyniesie:

zł

Oprocentowanie składane

Rachunek oprocentowania składanego polega na tym, że kwota odsetek w każdym okresie obliczeniowym powiększa podstawę naliczania odsetek dla okresu następnego. Dla rocznego okresu oprocentowania rachunek ten przedstawia się następująco:

po pierwszym roku
(10.5)

po drugim roku
(10.6)

po n - tym roku
(10.7)

Wyrażenie (1+r)ⁿ = b_n nazywamy współczynnikiem oprocentowania (załącznik 1). Korzystając z współczynnika b_n można obliczyć wartość końcową k_n przy pomocy wzoru:  

(10.8)

Przykład:

Kwota 10 000 zł ulokowana w banku, przy oprocentowaniu rocznym w wysokości 15% i kapitalizacji rocznej odsetek, po pięciu latach wyniesie:

zł

Wzór na oprocentowanie składane można wykorzystać nie tylko do wyznaczenia wartości k_n, ale także w przypadkach, gdy chcemy uzyskać informacje dotyczące:

• kwoty k_o, jaką należy zdeponować w banku aby po okresie n lat oraz przy oprocentowaniu rocznym r uzyskać kwotę k_n,

• okresu czasu, na jaki należy zdeponować w banku kwotę k_o, przy oprocentowaniu rocznym r, aby kapitał początkowy k_o powiększył się do kwoty k_n,

• wysokości oprocentowania r , na jaką należy złożyć kapitał k_o, tak aby po n latach wzrósł do wartości k_n.

Kapitał początkowy

Zakładamy, że po n latach od aktualnej chwili musimy dysponować kwotą k_n. Wiedząc, że oprocentowanie roczne w wybranym banku wynosi r, chcemy wiedzieć jaką kwotę k₀ musimy ulokować w banku, aby spełnić powyższe oczekiwanie. Wykorzystujemy w tym celu następujący wzór:

(10.9)

Przykład:

Jaką kwotę musimy ulokować w banku, przy oprocentowaniu rocznym w wysokości 15%, jeżeli za pięć lat chcemy dysponować kwotą 10 000 zł?

zł

Stopa procentowa

Aby obliczyć wysokość stopy procentowej, przy założonej kwocie k₀ oraz k_n i okresie oczekiwania n należy skorzystać ze wzoru:

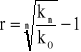
(10.10)

Przykład:

Jaka powinna być wielkość stopy oprocentowania, aby po wpłaceniu 50 000 zł, po pięciu latach uzyskać kwotę 120 000 zł ?

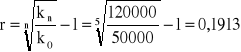
czyli 19,13%

Oprocentowanie składane z kapitalizacją odsetek w ciągu roku

Kapitalizacja odsetek, czyli dopisywanie odsetek do podstawy oprocentowania w rachunku oprocentowania składanego może być dokonywane nie tylko na koniec roku, ale również m. razy w ciągu roku. W takim przypadku stopę procentową dla każdego okresu kapitalizacji odsetek w ciągu roku możemy wyznaczyć według wzoru:

(10.11)

Kapitał początkowy k_o wyniesie:

po pierwszym okresie pierwszego roku:

(10.12)

po drugim okresie pierwszego roku:

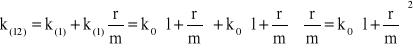
(10.13)

po m - tym okresie, czyli na koniec pierwszego roku:

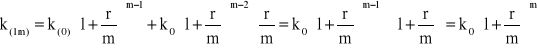
(10.14)

W następnych latach kapitalizacja odsetek również będzie dokonywana m razy w ciągu roku. Pod koniec kolejnego roku kapitał początkowy wzrośnie do kwoty:

po drugim roku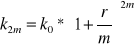
(10.15)

po n - tym roku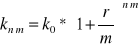
(10.16)

Przykład:

Bank oferuje oprocentowanie roczne 13% oraz kwartalną kapitalizację odsetek czyli m = 4. Zdeponowany w tym banku kapitał 10 000 zł po okresie dwóch lat wyniesie:

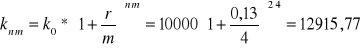
zł

Efektywna stopa procentowa

Efektywna stopa procentowa wynika z m.- krotnej kapitalizacji odsetek w ciągu roku, zaś jej wartość możemy wyznaczyć z wzoru:

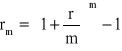
(10.17)

Przykład:

Oferowana przez bank efektywna stopa procentowa, przy nominalnej stopie procentowej r = 12%, oraz miesięcznej kapitalizacji odsetek w ciągu roku wyniesie:

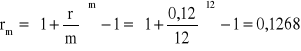
zł,

czyli 12,68%

Dyskontowanie proste

Jeżeli k_n jest kapitałem, którym będziemy dysponować w przyszłości, to jego aktualną wartość obliczymy korzystając ze wzoru:

(10.18)

Przykład:

Ile wyniesie aktualna wartość 15 000 zł, po okresie trzech lat przy nominalnej stopie procentowej 20%?

zł

Dyskontowanie składane

Aktualną wartość kapitału obliczymy ze wzoru:

(10.19)

Współczynnik
(10.20) nazywany jest współczynnikiem dyskontującym. W obliczeniach praktycznych podany jest w postaci tablicy (załącznik 2).

Przykład:

Za dwa lata wartość nieruchomości wzrośnie do 2 000 000 zł. Aktualną wartość nieruchomości, przy rocznej stopie procentowej 15% wyznaczymy w następujący sposób:

zł

Wartość kapitału zdyskontowaną na aktualny moment czasowy z kapitalizacją odsetek w ciągu n lat i m. okresów w ciągu roku wyznaczymy ze wzoru:

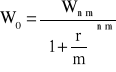
(10.21)

Współczynnikiem dyskontującym w tym przypadku jest wyrażenie;

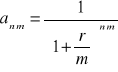
(10.22)

Przykład:

Jaką wielkość kapitału należy zdeponować w banku, który oferuje oprocentowanie 18% oraz comiesięczną kapitalizację odsetek, aby po dwóch latach otrzymać kwotę 70 000 zł?

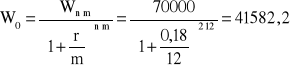
zł

Zadania do wykonania

Zadanie 1

Oblicz poniższe wartości używając równań, a następnie rozwiąż zadania przy pomocy tablic, aby sprawdzić poprawność odpowiedzi.

1. Podaj wartość przyszłą 5000 zł kapitalizowanych przez rok na 6%.

2. Podaj wartość przyszłą 5000 zł kapitalizowanych przez 10 lat na 12%.

3. Podaj wartość obecną 5000 zł należnych za rok przy 6% stopie dyskontowej.

4. Podaj wartość obecną 5000 zł należnych za 10 lat przy 12% stopie dyskontowej.

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Zadanie 2

Oblicz sumę, do której urośnie 5000 zł w każdej z następujących sytuacji:

1. 12% odsetek kapitalizowanych półrocznie przez 5 lat,

2. 12% odsetek kapitalizowanych kwartalnie przez 5 lat,

3. 12% odsetek kapitalizowanych miesięcznie przez 5 lat.

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Zadanie 3

Oblicz wartość obecną 5000 zł należnych w przyszłości w następujących sytuacjach:

1. Stopa nominalna 12%, kapitalizacja półroczna, dyskontowanie 5 lat wstecz,

2. Stopa nominalna 12%, kapitalizacja kwartalna, dyskontowanie 5 lat wstecz,

3. Stopa nominalna 12%, kapitalizacja miesięczna, dyskontowanie 5 lat wstecz.

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Zadanie 4

Która kwota jest warta więcej przy oprocentowaniu wynoszącym 14%:

1. 10 000 zł dzisiaj,

2. 20 000 zł należnych za 6 lat.

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Zadanie 5

Podaj z przybliżeniem do 1 roku, jak długo trzeba czekać na podwojenie sumy 200 zł, jeżeli jest ona złożona na rachunku przy następujących stopach procentowych:

a) 7%, b) 10% c) 18%

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Zadanie 6

Bank A płaci 7% odsetek kapitalizowanych rocznie na rachunkach terminowych. Bank B płaci 6% odsetek kapitalizowanych kwartalnie.

1. Opierając swój wybór na efektywnych stopach procentowych, w którym banku wolałbyś złożyć swoje pieniądze?

2. Czy fakt, że być może będziesz chciał wycofać pieniądze w ciągu roku, a nie po jego upływie, będzie miał wpływ na wybór banku? Załóż, że fundusze muszą być zdeponowane na rachunku przez cały okres kapitalizacji, abyś otrzymał odsetki.

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Zadanie 7

Firma Atlantic zainwestowała 4 mln dol. w celu wykarczowania działki i zasadzenia na niej młodych drzew. Drzewa wyrosną za 10 lat i wówczas firma spodziewa się sprzedać ten las za 8 mln dol. Jaka jest oczekiwana stopa dochodu firmy?

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Zadanie 8

Przedsiębiorca pewnej firmy obliczył, że po uruchomieniu nowej linii produkcyjnej osiągnie po drugim roku produkcji przychód ze sprzedaży w ilości 10 000 zł. Ile wynosi aktualna wartość przewidywanego przychodu przy nominalnej stopie procentowej 15%?

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

.................................................................................................................................................................

Ćwiczenie nr 11:

Próg rentowności

Analiza progu rentowności stanowi niezwykle pomocny instrument zarządzania przedsiębiorstwem w gospodarce rynkowej. Obejmuje ona badanie tzw. punktu wyrównania (break even point -BEP), w którym realizowane przychody ze sprzedaży dokładnie pokrywają poniesione koszty. Przedsiębiorstwo nie osiąga wówczas zysku, ale też nie ponosi straty. Rentow­ność sprzedaży jest równa zero, co oznacza, że firma osiągnęła próg rentow­ności.

Metoda analizy progu rentowności opiera się na podziale ogółu kosztów na stałe i zmienne. Stwarza to pewne ograniczenie wykorzystania jej w przed­siębiorstwach prowadzących rachunek kosztów oparty na innych zasadach. Pomimo to, jest ona coraz powszechniej stosowana.

Próg rentowności może być wyrażony ilościowo lub wartościowo. Może on ponadto informować, jaką część zdolności produkcyjnej (lub przewidywa­nego popytu) trzeba wykorzystać, aby ponoszone koszty zrównoważyć przy­chodami ze sprzedaży. Do wyznaczenia progu rentowności możemy zastosować odpowiednie równania matematyczne lub posłużyć się metodą graficzną. W obu przypadkach przyjmujemy następujące założenia upraszczające:

• wartość produkcji w badanym okresie jest równa wartości sprzedaży,

• koszty produkcji są funkcją wielkości produkcji,

• stałe koszty produkcji są jednakowe dla każdej wielkości produkcji,

• jednostkowe koszty zmienne są stałe i wskutek tego całkowite koszty zmienne produkcji zmieniają się proporcjonalnie do wielkości produkcji,

• jednostkowe ceny sprzedaży poszczególnych wyrobów nie ulegają zmianie z upływem czasu i nie zmieniają się również wraz ze zmianą skali produkcji w całym badanym okresie; wartość sprzedaży jest więc funkcją liniową jednostkowej ceny sprzedaży i ilości sprzedanych wyrobów,

• poziom jednostkowych kosztów zmiennych i stałych kosztów produkcji pozostaje niezmieniony w całym badanym okresie.

Próg rentowności przy produkcji jedno asortymentowej

Na poziom tego progu rentowności wpływają wówczas następujące czynniki: wielkość produkcji (sprzedaży), cena wyrobu, jednostkowe koszty zmienne, stałe koszty produkcji.

Znając ich wielkość tych czynników, możemy obliczyć:

• wartość sprzedaży według równania:

S = P * c (11.1)

gdzie:

S - wartość sprzedaży,

P - ilość sprzedanych wyrobów,

c -jednostkowa cena sprzedaży,

• poziom kosztów całkowitych według równania:

Kc = Ks + P * kz (11.2)

gdzie:

Kc - całkowite koszty produkcji,

Ks - stałe koszty produkcji,

kz - jednostkowe koszty zmienne,

- pozostałe oznaczenia jak we wzorze (11.1).

Próg rentowności znajduje się w punkcie, w którym wartość sprzedaży jest równa poziomowi kosztów całkowitych, a więc:

S = Kc, ⇒ P * c = Ks + P * kz (11.4)

Gdzie wszystkie oznaczenia jak we wzorach powyżej. Przekształcając powyższe równanie obliczymy próg rentowności w wy­rażeniu:

• ilościowym:

(11.5)

gdzie:

BEP - próg rentowności w wyrażeniu ilościowym,

• wartościowym:

(11.6)

gdzie:

BEP'­ - próg rentowności w wyrażeniu wartościowym,

• jako stopień wykorzystania zdolności produkcyjnej (lub stopień zaspoko­jenia przewidywanego popytu):

(11.7)

gdzie:

BEP" - próg rentowności (procentowy),

P_m - maksymalna ilość sprzedanych wyrobów określona na podstawie zdolności produkcyjnej lub prognozy popytu,

Na podstawie równań wartości sprzedaży oraz kosztów całkowitych możliwe jest również graficzne wyznaczenie progu rentowności (rys. 11).

Schemat ten obrazuje ilościowy i wartościowy próg rentowności. Pozwala on również ocenić, jaką część zdolności produkcyjnej należy wykorzystać dla osiągnięcia progu rentowności. Porównanie krzywej wartości sprzedaży i kosz­tów całkowitych umożliwia ponadto ustalenie przewidywanego poziomu zysku, w zależności od zrealizowanej wielkości sprzedaży. Przy pełnym wykorzystaniu zdolności produkcyjnej zysk ten wyniesie:

Z_m = P_m. * c - (Ks + P_m. * kz) (11.8)

gdzie:

Z_m - poziom zysku przy pełnym wykorzystaniu zdolności produkcyjnej (lub pełnym zaspokojeniu przewidywanego popytu),

- pozostałe oznaczenia, jak we wzorach (11.1), (11.2) i (11.7).

Sposób obliczania progu rentowności przy produkcji jednoasortymentowej zilustrujemy przykładem.

Rys. 11. Graficzne wyznaczenie progu rentowności

Przykład

Przedsiębiorstwo produkuje jeden wyrób. Koszty jednostkowe zmienne tego wyrobu wynoszą 440 tys. zł/szt. Przewiduje się, że przy cenie 580 tys. zł/szt. efektywny popyt wyniesie 24000 szt. W ciągu roku. Stałe koszty funkcjonowania przedsiębiorstwa kształtują się na poziomie 1 330 mln zł rocznie.

Próg rentowności przedsiębiorstwa obliczony na podstawie równań (11.5), (11.6) i (11.7) wynosi:

BEP' = 9500x580 = 5510000 tys. zł

Obliczenie progu rentowności przedsiębiorstwa stwarza szerokie możliwości dalszej analizy. Obejmuje ona przede wszystkim ocenę kształtowania się rentowności w przypadku zmian poszczególnych czynników wpływających na jej poziom. Szczególne znaczenie ma przy tym zbadanie:

• jaki ewentualny spadek popytu na produkowane wyroby może doprowadzić do całkowitej utraty rentowności przez przedsiębiorstwo,

• jakie są możliwości zwiększenia zysku przedsiębiorstwa poprzez kształtowanie czynników określających jego poziom.

Przedsiębiorstwo funkcjonujące w gospodarce rynkowej narażone jest stale na niebezpieczeństwo spadku sprzedaży wyrobów na skutek zmian warunków rynkowych. Stąd celowe jest ustalenie tzw. wskaźnika bezpieczeńs­twa, obrazującego wrażliwość przedsiębiorstwa na spadek popytu zgłaszanego przez rynek na jego wyroby. Wskaźnik ten obliczymy na podstawie równania:

(11.9)

gdzie:

W_b - wskaźnik bezpieczeństwa,

- pozostałe oznaczenia jak we wzorze (11.7).

Jeżeli do osiągnięcia progu rentowności konieczne jest zaspokojenie pełnego popytu, to W_b = O (zero). Oznacza to, że już w chwili obecnej przedsiębior­stwo nie osiąga zysku. Każdy spadek popytu na produkowane wyroby przyniesie więc stratę. Z kolei im wyższy wskaźnik bezpieczeństwa (W_b → 1), tym większy spadek popytu może ono przetrwać nie ponosząc strat. Przyk­ładowo W_b = 0,5 oznacza, że nawet spadek popytu o 50% nie spowoduje straty, chociaż zredukuje zysk przedsiębiorstwa do zera.

Ważną informacją dla bieżącego zarządzania przedsiębiorstwem jest również zbadanie potencjalnych możliwości podniesienia jego rentowności. Możliwości te tkwią zarówno po stronie przychodów ze sprzedaży, jak i po stronie kosztów.

Na podstawie danych przykładu 1 zbadamy, czy podniesienie ceny do poziomu 620 tys. zł/szt. będzie dla przedsiębiorstwa opłacalne, jeżeli przyniesie spadek popytu do poziomu 20000 szt. rocznie. Przy pełnym zaspokojeniu tego popytu przedsiębiorstwo osiągnie zysk:

Z'_m = 2 0000 * 620­ - (1 330 000 + 20000 * 440) = 2 270 000 tys. zł.

W sytuacji wyjściowej zysk realizowany przy sprzedaży 24 000 szt. Wyrobów wynosił 2 030 mln zł, był więc niższy o 240 mln zł w stosunku do zysku osiągniętego po zmianie ceny, co uzasadnia jej podwyższenie.

Możliwości podniesienia rentowności przedsiębiorstwa tkwią również w dążeniu do obniżenia zarówno stałych, jak i zmiennych elementów kosztów. W każdym przypadku prowadzi to do zwiększania poziomu realizowanego zysku.

Obniżenie poziomu kosztów nie tylko zwiększa rentowność przedsiębior­stwa, lecz przyczynia się również, poprzez zmniejszenie progu rentowności, do rozszerzenia marginesu bezpieczeństwa. Wzrost kosztów wywoła natomiast przeciwne skutki. Wskazuje to na potrzebę stałej kontroli poziomu kosztów i szukania możliwości ich obniżenia.

Zadania do wykonania

Wyznaczyć wielkość progu rentowności produkcji dla poniższych danych

Sprzedaż w kraju - 1 800 000 szt/rok,

Sprzedaż na eksport - 750 000 szt/rok,

Zdolności produkcyjne - 2 850 000 szt/rok.

Cena zbytu:

Wariant 1	Jednostka	A	B	C	D	E
Cena zbytu na kraj	zł/szt	221,07	226,29	231,90	230,03	210,26
Cena zbytu na eksport	zł/szt	152,07	153,29	154,90	156,03	157,26

Wariant 2	Jednostka	A	B	C	D	E
Cena zbytu na kraj	zł/szt	211,07	215,29	233,90	245,03	190,26
Cena zbytu na eksport	zł/szt	155,10	155,68	157,30	158,35	159,58

Wariant 3	Jednostka	A	B	C	D	E
Cena zbytu na kraj	zł/szt	195,07	202,29	205,90	210,03	215,26
Cena zbytu na eksport	zł/szt	148,63	148,40	150,02	151,20	152,60

Koszt sprzedaży: [mln. zł]

Wyszczególnienie	Udział kosztu stałego w koszcie ogółem	A	B	C	D	E
Amortyzacja	100%	28,655	27,743	42,004	39,155	34,640
Zużycie materiałów	30%	84,252	84,252	84,914	85,241	83,679
Energia	0%	34,945	34,420	33,531	33,260	33,260
Usługi	80%	76,749	75,662	75,124	74,147	70,815
Wynagrodzenia z narzutami	90%	229,272	220,102	213,319	206,228	195,748
Opłaty oraz podatki	35%	20,639	21,111	21,997	22,065	23,095
Ubezpieczenia	100%	15,091	13,929	14,181	13,067	12,072
Pozostałe koszty	80%	30,959	31,293	30,616	29,826	29,070
Razem		520,562	508,512	515,686	502,989	482,379

Wyznaczenie progu rentowności dla produkcji jednolitej metodą analityczną:

Wyznaczenie progu rentowności dla produkcji jednolitej metodą graficzną:

P(0) = P(zp) =

Kc(0) = Kc(zp) =

Ćwiczenie nr 12:

Okres zwrotu nakładów, wartość kapitałowa

OKRES ZWROTU NAKŁADÓW INWESTYCYJNYCH

Technika ta polega na określaniu czasu, w jakim następuje zrównanie przewidywanych nakładów inwestycyjnych z nadwyżkami finansowymi, których uzyskania oczekuje się dzięki realizacji danego projektu. Okres zwrotu nakładów inwestycyjnych można ustalić, kompensując stopniowo ich wielkość kolejnymi corocznymi kwotami przewidywanych nadwyżek finansowych. Za bardziej efektywne uważa się projekty, które zapewniają najkrótszy okres zwrotu nakładów inwestycyjnych. Przyjmuje się zatem założenie, ze im wcześniej zostaną wycofane zainwestowane kapitały, tym mniejsze jest ryzyko związane z danym projektem. Jednocześnie zwolnione wcześniej kapitały można przeznaczyć na finansowanie innych przedsięwzięć inwestycyjnych.

PRZYKŁAD

Spółka rozważa dwie alternatywy inwestycyjne w celu zwiększenia zysków. Pierwsza wymaga nakładów inwestycyjnych w wysokości 28.000 tys. zł, a okres eksploatacji inwestycji wynosiłby 5 lat. Druga łączy się z koniecznością poniesienia nakładów 35.000 tys. zł, a okres eksploatacji inwestycji wydłużyłby się do 7 lat. Przewidywana nadwyżka finansowa (zysk netto plus amortyzacja) w poszczególnych latach eksploatacji rozpatrywanych obiektów i jej porównanie z kalkulowanymi nakładami inwestycyjnymi przedstawia się jak w tablicy 5

Kalkulacja wskazuje, że obie alternatywy są opłacalne. Jednak w razie realizacji pierwszej alternatywy zwrot nakładów inwestycyjnych nastąpiłby po upływie 3,5 roku. Dla drugiej alternatywy przewidywany okres zwrotu wynosi 4 lata. Wobec tego z punktu widzenia kryterium czasu zwrotu nakładów inwestycyjnych korzystniejsza jest alternatywa I.

Przedstawiona metoda jest łatwa do stosowania i cechuje się znaczną przejrzystością. Posługiwanie się nią może jednak prowadzić do błędnej decyzji, gdyż nie uwzględnia ona faktu zmiennej wartości pieniądza w czasie. Wydatki inwestycyjne są bowiem ponoszone do momentu zakończenia inwestycji, natomiast oczekiwane nadwyżki finansowe, które mają być wygospodarowane dzięki realizacji rozpatrywanych projektów, będą realizowane stopniowo. Im dłużej trzeba oczekiwać na uzyskanie nadwyżki, tym mniejsza jest zatem jej aktualna wartość.

Tablica 5. Zwrotność nakładów inwestycyjnych w nominalnym ujęciu

Koniec roku Nakłady	Alternatywa I		Alternatywa II
		Nadwyżka roczna	Nakłady skompensowane nadwyżką	Nadwyżka roczna	Nakłady skompensowane nadwyżką
0	-	28.000	-	35.000
1	8.000	- 20.000	8.000	- 27.000
2	8.000	- 12.000	8.000	- 19.000
3	8.000	- 4.000	9.000	- 10.000
4	8.000	+ 4.000	10.000	-
5	8.000	+ 12.000	18.000	+ 18.000
6	-	-	11.000	+ 29.000
7	-	-	4.000	+33.000
Razem	40.000	+ 12.000	68.000	+33.000

Powstaje zatem wątpliwość czy rozpatrywane projekty inwestycyjne zapewniają osiągnięcie z góry zakładanej stopy zyskowności poniesionych nakładów, tj. czy preliminowane nadwyżki finansowe pokryją nie tyko zwrot ale także koszt zaangażowanego kapitału ulokowanego w danych projektach. Te niedoskonałości mogą być usunięte w razie zastosowania rachunku uwzględniającego aktualizację wartości kalkulowanych nadwyżek finansowych (dyskonto), tj. sprowadzenia ich do realnego poziomu, odpowiadającego poziomowi aktualnej wartości przewidywanych nakładów inwestycyjnych.

AKTUALNA WARTOŚĆ NADWYŻKI FINANSOWEJ NETTO

Metoda ta polega na konfrontacji przewidywanych na realizację projektów nakładów ze spodziewanymi nadwyżkami finansowymi, ale po uprzednim sprowadzeniu ich wartości do aktualnego poziomu, uwzględniając określony z góry koszt zaangażowania kapitału (postulowaną zyskowność inwestycji). Już we wstępnej fazie kalkulacji trzeba zatem określić pożądaną stopę oprocentowania (koszt) kapitałów niezbędnych na realizację inwestycji. Koszt tego oprocentowania powinny pokryć oczekiwane nadwyżki finansowe niezależnie od zwrotu nakładów. Następnie - przy zastosowaniu pożądanej stopy oprocentowania - dyskontuje się kwoty nadwyżek finansowych preliminowanych na poszczególne lata uwzględniając rachunek procentu składanego. Obliczenia można dokonywać na podstawie wzoru:

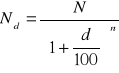
(12.1)

gdzie:

N - nadwyżka finansowa w nominalnej wysokości,

N_d - nadwyżka finansowa preliminowana na dany rok po zdyskontowaniu (aktualna wartość nadwyżki),

d - stopa oprocentowania, tj. kosztu (postulowanej zyskowności) kapitału (preliminowanych nakładów inwestycyjnych).

Znacznym ułatwieniem jest posługiwanie się tablicami zawierającymi już gotowe obliczone wskaźniki dyskonta kapitału na końcu podręcznika.

Posługując się tymi współczynnikami można ustalić zdyskontowane dla poszczególnych lat kwoty nadwyżek według formuły:

N_d = N x V (12.2)

gdzie:

N_d - zdyskontowana nadwyżka finansowa danego roku,

N - pierwotna kwota nadwyżki finansowej danego roku,

V - współczynnik dyskonta dla określonego roku przy danej stopie dyskonta.

PRZYKŁAD

Założenia wstępne są analogiczne jak w poprzednim przykładzie, ale przyjmuje się dodatkowo, że opłacalne będą projekty zapewniające zwrot poniesionych nakładów przy stopie co najmniej 18% rocznie. Wobec tego kalkulacja opłacalności obu rozpatrywanych uprzednio alternatyw inwestycyjnych kształtuje się jak w tablicy 6.

Tablica 6. Nadwyżka finansowa netto dla rozpatrywanych wariantów inwestycji

Koniec roku	Współczynnik dyskonta dla 18%	Alternatywa I		Alternatywa II
				Nadwyżki finansowe
				nominalne	zdyskonto-wane	nominalne	zdyskonto-wane
1	0.847458	8.000	6.780	8.000	6.780
2	0.718184	8.000	5.745	8.000	5.745
3	0.608631	8.000	4.869	9.000	5.478
4	0.515789	8.000	4.126	10.000	5.158
5	0.437109	8.000	3.497	18.000	7.868
6	0.370432	-	-	11.000	4.075
7	0.313925	-	-	4.000	1.256
Razem nadwyżka Nakłady inwestycyjne		40.000 -	25.017 28.000	68.000 -	36.360 35.000
Różnica			- 2.983		+ 1.360

Dane kalkulacji informują, że alternatywa pierwsza nie zapewnia pełnego zwrotu nakładów inwestycyjnych przy postulowanej minimalnej stopie zyskowności zaangażowania kapitału. Zwrot taki - nawet z pewną nadwyżką - zapewnia projekt drugi i wobec tego on może być realizowany.

Jak wynika z przykładu, przy posługiwaniu się metodą oceny projektów inwestycyjnych na podstawie aktualnej wartości nadwyżki finansowej netto (ang. net present value - NPV), za efektywne uznaje się alternatywy, przy których suma zdyskontowanych nadwyżek przekracza lub co najmniej wyrównuje preliminowane nakłady początkowe.

Zadania do wykonania

Zadanie 1

Firma „Xon” rozważa zainwestowanie wolnych środków w trzy alternatywne przedsięwzięcia. Dla poniżej przedstawionych wielkości nadwyżki finansowej w poszczególnych wariantach określić okres zwrotu nakładów inwestycyjnych.

Wielkość nakładów finansowych oraz nadwyżki finansowej

Rozwiązanie

Okres zwrotu nakładów:

Wariant 1 - ..................................

Wariant 2 - ..................................

Wariant 3 - ..................................

Zadanie 2

Założenia wstępne jak powyżej.

Oprocentowanie nakładów inwestycyjnych: ................. %

Nadwyżka finansowa wynosi zatem:

Wariant 1 - ..................................

Wariant 2 - ..................................

Wariant 3 - ..................................

Literatura

1. Bellman R.E., Dreyfus S. E.: „Programowanie dynamiczne”; Państwowe Wydawnictwa Ekonomiczne, W-wa, 1967.

2. Bień W.: Ocena efektywności finansowej spółek prawa handlowego”; Finans - Servis, W-wa, 1997 r.

3. Bladkowski S.: „Metody sieciowe w planowaniu i organizacji pracy”; PWE, Warszawa, 1970 r.

4. Burton C., Michael N.: „Zarządzanie projektem - jak to robić w twojej organizacji”; Wydawnictwo Astrum, Wrocław, 1999 r.

5. Dietrych J.: „Projektowanie i konstruowanie”; WNT, W-wa, 1974 r.

6. Duraj J.: „Analiza ekonomiczna przedsiębiorstwa”; PWE, W-wa, 1993 r.

7. Flak W., Henzel H., Krotka W., Marcinek K., Stosur E., Walica H.: „Vademecum inwestora”; GIPH, 1996 r.

8. G.H. Mitchell: „Badania operacyjne”; Wydawnictwa Naukowo - Techniczne, W-wa, 1977 r.

9. Jachna T., Sierpińska M.: „Ocena przedsiębiorstwa według standardów światowych”; Wydawnictwo Naukowe PWN, wydanie I, W-wa, 1993 r.

10. Jędrzejczyk Z., Kukuła K., Skrzypek J., Walkosz A.: „Badania operacyjne w przykładach i zadaniach”; Wydawnictwo Naukowe PWN, wydanie III, W-wa, 1999 r.

11. Jones J. Ch.: „Metody projektowania”; WNT, W-wa, 1977 r.

12. Karbownik A.: „Podstawy projektowania kopalń - część I: Ocena rozwiązań projektowych”; Skrypty Uczelniane Politechniki Śląskiej nr 1318, Gliwice, 1986 r.

13. Karbownik A.: „Podstawy teorii projektowania”; Skrypty Uczelniane Politechniki Śląskiej nr 1364, Gliwice, 1987 r.

14. Kowalski R.: „Logika w rozwiązywaniu zadań”; WNT, W-wa, 1989 r.

15. MCSP UNIDO: „Poradnik przygotowania analizy przemysłowych projektów inwestycyjnych”; Biuro UNIDO w W-wie, 1989 r.

16. Tarnowski W.: „Metody koncypowania - Heurystyczne metody poszukiwania rozwiązań projektowych”; Skrypty Uczelniane Politechniki Śląskiej nr 1277, Gliwice, 1986 r.

17. Tarnowski W.: „Podstawy projektowania technicznego”; seria Wspomaganie Komputerowe CAD/CAD, WNT, W-wa, 1997 r.

Ze względu na ograniczenie czasowe analizę problemu progu rentowności dla produkcji wieloasortymentowej pozostawiamy do samodzielnego zbadania.

Podstawy Projektowania Inżynierskiego

Przewodnik po ćwiczeniach

50

51

4

2

1

7

5

3

6

t

i

T

L

5

29

24

6

5

15

10

3

0

29

29

7

0

26

26

5

1

26

25

4

0

20

20

2

0

0

0

1

a

20

b

10

c

5

e

14

d

6

f

3

f

3

d

3

e

14

c

3

b

10

a

20

2

26

24

6

2

12

10

3

0

26

26

7

0

23

23

5

0

20

20

2

0

0

0

1

0

23

23

4

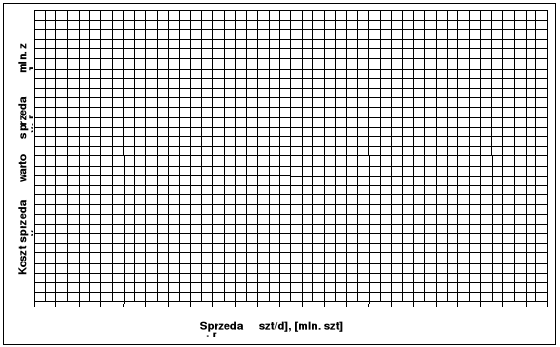
NIE

TAK

NIE

TAK

Δ = 0

?

Δ > 0

?

STOP

Brak rozwiązania

Δ = b²-4ac

Dane: a, b, c

START

Rys. 3. Przykład pętli w algorytmie

Zwiększyć wartość licznika o 1

NIE

TAK

Instrukcje

Wartość licznika = 0

Koniec pętli

?

Rys. 2. Przykład operacji logicznej w algorytmie

X max = X

NIE

TAK

X max < X ?

Wyjście lub wejście z wyodrębnionych fragmentów na różnych stronach

Wyjście lub wejście z wyodrębnionych fragmentów na tej samej stronie

Początek, koniec

Decyzja

Dane, wyniki

Instrukcja

Kc=Ks+P*kz

zysk

S=P*c

strata

Z_m

100%

Pm

BEP''

BEP

Ks

BEP'

Zdolność produkcyjna (lub prognoza popytu)

Wielkość sprzedaży

Wartość sprzedaży

Koszty całkowite

r opt

r op 2

r op 1

r extr

F

r

Uzyskany rezultat poszukiwania ekstremum

F

r

Poszukiwane

minimum

e

14

d

6

f

3

c

5

b

10

a

20

---