METODY PORZĄDKOWANIA LINIOWEGO

Metody porządkowania liniowego

• porządkowanie liniowe obiektów polega, w ujęciu geometrycznym, na rzutowaniu punktów reprezentujących obiekty umieszczonych w wielowymiarowej przestrzeni zmiennych na prostą

• pozwala na ustalenie hierarchii obiektów, czyli uporządkowanie ich od obiektu stojącego najwyżej w tej hierarchii do obiektu znajdującego się w niej najniżej

Metody porządkowania nieliniowego

• porządkowanie nieliniowe polega, od strony geometrycznej, na rzutowaniu obiektów umieszczonych w wielowymiarowej przestrzeni zmiennych na płaszczyznę

• nie pozwala na ustalenie hierarchii obiektów lecz tylko na określenie dla każdego z obiektów, obiektów do niego podobnych

PORZĄDKOWANIE LINIOWE

Własności uporządkowania liniowego

• każdy obiekt ma przynajmniej jednego sąsiada i nie więcej niż dwóch sąsiadów

• jeżeli sąsiadem i-tego obiektu jest i'-ty obiekt to jednocześnie sąsiadem i'-tego obiektu jest i-ty obiekt

• dokładnie dwa obiekty mają tylko jednego sąsiada

GRUPY METOD PORZĄDKOWANIA LINIOWEGO

• metody diagramowe - w metodach diagramowych stosuje się graficzną prezentację macierzy odległości zwaną diagramem

• procedury oparte na zmiennej syntetycznej

• bezwzorcowe - w metodach bezwozrcowych zmienna syntetyczna jest funkcją znormalizowanych wartości zmiennych wejściowych

• metody te wymagają wcześniejszej stymulacji zmiennych wejściowych

• wzorcowe - w metodach wzorcowych wykorzystywane jest pojęcie obiektu wzorcowego, czyli obiektu modelowego o porządanych wartościach zmiennych wejściowych

• miara syntetyczna konstruowana jest na podstawie odległości pomiędzy obserwowanym obiektem, a obiektem wzorcowym.

• metody iteracyjne - w metodach iteracyjnych przyjmowana jest funkcja kryterium dobroci grupowania i w kolejnych iteracjach szukamy takiego uporządkowania liniowego obiektów, które optymalizują wartość funkcji kryterium aż do osiągnięcia przez nią wartości optymalnej (maksymalnej lub minimalnej)

METODY DIAGRAMOWE

METODA CZEKANOWSKIEGO

Procedura wykorzystująca ocenę wzrokową dobroci uporządkowania

• punkt wyjścia metody Czekanowskiego stanowi macierz odległości między obiektami D[d_ii'], zdefiniowana za pomocą dowolnej metryki

• mierniki odległości w macierzy odległości D dzieli się na klasy podobieństwa obiektów

• poszczególnym klasom podobieństwa obiektów przyporządkowuje się odpowiednie symbole graficzne, otrzymując nieuporządkowany diagram Czekanowskiego, co pozwala na wzrokową ocenę przebiegu porządkowania obiektów

• samo porządkowanie obiektów odbywa się poprzez porządkowanie diagramu, polegające na przestawianiu wierszy i odpowiadających im kolumn diagramu tak aby symbole graficzne reprezentujące możliwe najmniejsze odległości skupiały się wzdłuż głównej przekątnej, a w miarę oddalania się od głównej przekątnej pojawiały się symbole graficzne odpowiadające coraz większym odległościom

• kolejność uporządkowania obiektów jest określona przez kolejność odpowiadających im wierszy (kolumn)

Procedura wykorzystująca funkcję dobroci uporządkowania

Funkcja dobroci uporządkowania

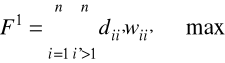
, (2.1)

gdzie:

w_ii' - wagi elementów macierzy odległości, zdefiniowane w oparciu o jeden z następujących wzorów:

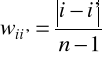
, (2.2)

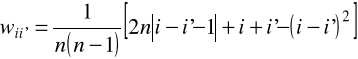
, (2.3)

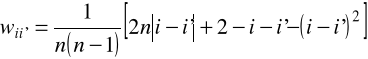
. (2.4)

Wagi elementów macierzy odległości

• wagi elementów macierzy odległości tworzą macierz wag o postaci:

, i,i'=1,2,...,n. (2.5)

• wagi w macierzy W są rozmieszczone zgodnie z pożądanym rozmieszczeniem elementów w macierzy odległości D (macierz W stanowi wzorzec dla docelowego uporządkowania diagramu powstałego z macierzy odległości D)

• porządkując diagram Czekanowskiego przestawimy w nim wiersze i odpowiednie kolumny w taki sposób aby były ułożone zgodnie ze wzorem wag w macierzy W, co osiąga się maksymalizując funkcję poprawności uporządkowania (2.1).

Etapy procedury porządkowania diagramu Czekanowskiego

• punktem wyjścia jest wyznaczenie wartości miernika poprawności uporządkowania (2.1) dla początkowego uporządkowania obiektów

• pierwszy krok procedury rozpoczynamy od transpozycji dwóch pierwszych obiektów ponownie obliczając wartość funkcji kryterium

• w przypadku gdy wartość funkcji kryterium nie wzrośnie wracamy do poprzedniego uporządkowania. Gdy natomiast nastąpi wzrost wartości funkcji kryterium traktuje się dane uporządkowane jako wyjściowe dla dalszych etapów i analogicznie transpozycje przeprowadzamy dla kolejnych par obiektów (drugiego i trzeciego, trzeciego i czwartego itd., kończąc na transpozycji obiektów (n-1)-szego i n-tego) sprawdzając za każdym razem czy nie nastąpił wzrost wartości funkcji kryterium;

• po przeprowadzeniu pierwszej iteracji sprawdzamy, czy w jej wyniku nie nastąpiły jakieś zmiany w uporządkowaniu obiektów

• gdy zmiany nie nastąpiły uporządkowanie obiektów uważa się za ostateczne. W przypadku zaistnienia takich zmian przechodzi się do kolejnej iteracji porządkowania traktując uporządkowanie z poprzedniej iteracji jako wyjściowe

• proces porządkowania obiektów kończymy gdy w danej iteracji nie nastąpiły zmiany w uporządkowaniu obiektów w stosunku do poprzedniej iteracji

METODY OPARTE NA ZMIENNYCH SYNTETYCZNYCH

METODY BEZWZORCOWE

Formuły wyznaczania zmiennej syntetycznej:

• dla średniej arytmetycznej:

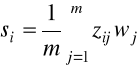
, i=1,2,...,n, (2.6)

• dla średniej geometrycznej:

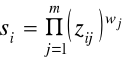
, i=1,2,...,n, (2.7)

• dla średniej harmonicznej:

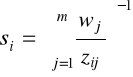
, i=1,2,...,n, (2.8)

gdzie:

s_i - wartość zmiennej syntetycznej w i-tym obiekcie.

METODA RANG

• na wstępie dokonujemy stymulacji zmiennych

• w kolejnym kroku dla każdego obiektu wyznacza się sumę przyporządkowanych mu rang, ze względu na wszystkie zmienne. Gdy dana wartość zmiennej występuje w więcej niż jednym obiekcie, przyporządkowujemy im jednakową rangę będącą średnią arytmetyczną z przysługujących im rang

• obliczamy wartości zmiennej syntetycznej jako średnią wartość rang według formuły:

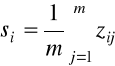
, i=1,2,...,n, (2.9)

gdzie z_ij jest unormowana według formuły (1.31).

METODA SUM

• w pierwszym etapie metody dokonujemy stymulacji zmiennych

• następnie obliczamy wartości zmiennej syntetycznej dla każdego obiektu stosując formułę średniej arytmetycznej (2.6), przyjmując jednakowe wagi dla zmiennych

• w kolejnym kroku eliminujemy wartości ujemne zmiennej syntetycznej przesuwając jej skalę do punktu zerowego poprzez przekształcenie:

, i=1,2,...,n. (2.10)

• ostateczną postać zmiennej syntetycznej otrzymujemy przeprowadzając jej normalizację według formuły:

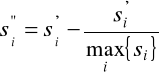
, i=1,2,...,n. (2.11)

• dokonane przekształcenia powodują unormowanie miary syntetycznej w przedziale [0,1]

METODY WZORCOWE

MIARA ROZWOJU

• na podstawie macierzy zestandaryzowanych danych wejściowych wyznacza się obiekt wzorcowy o współrzędnych (wystandaryzowanych wartościach zmiennych):

, j=1,2,...,m. (2.12)

• współrzędne obiektu wzorcowego wyznaczamy na podstawie następującej formuły:

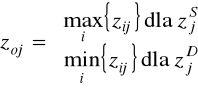
, j=1,2,...,m. (2.13)

• następnie obliczamy dla każdego obiektu jego odległość od obiektu wzorcowego, stosując najczęściej metrykę euklidesową o postaci:

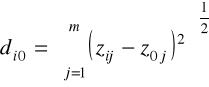
, i=1,2,...,m. (2.14)

• miara syntetyczna jest ostatecznie definiowana jako:

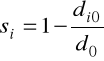
, i=1,2,...,m, (2.15)

gdzie:

, (2.16)

przy czym:

;
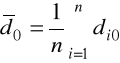
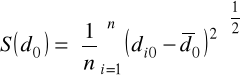
. (2.17)

• miara d_i przyjmuje zazwyczaj wartości z przedziału [0; 1]. Wartości te są tym wyższe im dany obiekt jest mniej oddalony od wzorca.

METODA DYSTANSOWA

• punktem wyjścia wyznaczania zmiennej syntetycznej jest obliczenie odległości (dystansu) od obiektu wzorca, dla każdego z porównywanych obiektów

• konstruujemy miarę syntetyczną, wykorzystująca formułę przekształcenia unitaryzacyjnego:

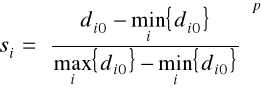
, i=1,2,...,m, (2.23)

gdzie p jest parametrem normalizacyjnym.

METODY INTERACYJNE

METODA SZCZOTKI

Założenie

Poszukiwane jest takie liniowe uporządkowanie obiektów, dla którego funkcja kryterium dobroci uporządkowania osiąga maksimum:

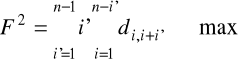
, (2.24)

gdzie:

d_i,i+i' - odległość euklidesowa między i-tym i i'-tym obiektem.

Etapy procedury

• punktem wyjścia procedury jest dowolne liniowe uporządkowanie obiektów, dla którego obliczamy wartość funkcji kryterium (2.24)

• następnie obliczamy wartości funkcji kryterium dla każdej możliwej transpozycji pary obiektów

• jeżeli wartości funkcji kryterium dla każdej z transpozycji par obiektów są mniejsze od wartości tej funkcji dla uporządkowania wyjściowego obiektów, uporządkowanie to uważamy za najlepsze. W przeciwnym razie dokonujemy transpozycji tej pary obiektów, dla której wzrost wartości funkcji kryterium jest największy

• uporządkowanie to stanowi punkt wyjścia do oceny, czy kolejna transpozycja dowolnej pary obiektów pozwoli na wzrost wartości funkcji kryterium

• powyższe postępowanie jest kontynuowane do momentu gdy transpozycja dowolnej pary obiektów nie prowadzi do wzrostu wartości funkcji kryterium

METODY GRADIENTOWE

• dążymy do takiego liniowego uporządkowania obiektów, które jak najmniej zniekształca relacje strukturalne porządkowanego zbioru obiektów

• od strony geometrycznej oznacza to, że odległości pomiędzy punktami reprezentującymi obiekty w przestrzeni jednowymiarowej, określonej przez zmienną syntetyczną, w jak najmniejszym stopniu zniekształcają odległości pomiędzy tymi punktami w przestrzeni wielowymiarowej, określonej przez zmienne wejściowe

• od strony formalnej szukamy takich współrzędnych punktów reprezentujących obiekty w przestrzeni jednowymiarowej, dla których funkcja dobroci uporządkowania osiąga minimum, co można przedstawić wariantowo następująco:

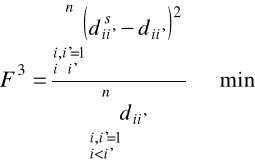
(2.25)

lub

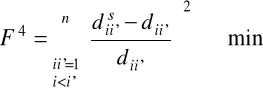
(2.26)

lub

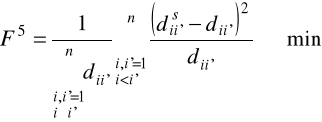
(2.27)

gdzie:

- odległość między i-tym i i'-tym obiektem w przestrzeni jednowymiarowej określonej przez szukaną zmienną syntetyczną.

Etapy procedury

• wyznaczamy wartość funkcji - kryterium dla wyjściowego, liniowego uporządkowania obiektów (wyjściowych wartości zmiennych syntetycznych w tych obiektach), traktując ją jak wynik interacji t=0:

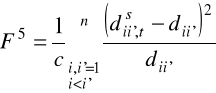
, (2.28)

gdzie:

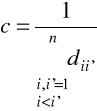
, (2.29)

przy czym zarówno wartości zmiennych oryginalnych jak i wyjściowych wartości zmiennych syntetycznych zostały znormalizowane na przedziale [0;1].

• współrzędne zmiennych syntetycznych dla obiektów w kolejnej iteracji t+1 wyznacza się w oparciu o wzór:

, (2.30)

gdzie:

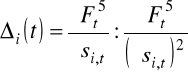
, (2.31)

przy czym:

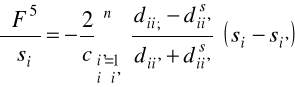
, (2.32)

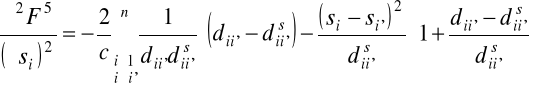
.(2.33)

• na wstępie zakłada się maksymalną oraz minimalną wartość parametru W (np. W_max=10 i W_min=0,1), wskaźnik skali zmian wartości tego parametru pomiędzy iteracjami (np. W_t+1/W_t=0,5) oraz maksymalną liczbę iteracji

• procedurę iteracyjną rozpoczynamy od przyjęcia maksymalnej wartości parametru W

• postępowanie iteracyjne jest kontynuowane do momentu gdy nastąpi wzrost wartości funkcji kryterium

• wtedy wracamy do wartości zmiennej syntetycznej z poprzedniej iteracji jednocześnie zmniejszają wartość parametru W o przyjęty wskaźnik jego zmian

• procedurę kontynuujemy do momentu, aż wartość parametru W nie spadnie poniżej założonej wartości minimalnej albo aż osiągniemy z góry założoną liczbę iteracji