ANALIZA KORESPONDENCJI

Ogólna charekterystyka:

pozwala na znalezienie punktów - zmiennych względem nowego układu odniesienia oraz punktów - obiektów względem tego samego układu odniesienia, co umożliwia opisanie zależności między zmiennymi i obiektami, na których przeprowadzono obserwację,

analiza związków pomiędzy zmiennymi i obiektami odbywa się w sposób bezpośredni w przeciwieństwie do analizy pośredniej poprzez związki zmiennych z czynnikami, jak ma to miejsce w pozostałych metodach czynnikowych,

na wykresy struktur czynnikowych już przeanalizowanych zmiennych i obiektów, można nanosić nowe punkty - zmienne i punkty-obiekty,

nie stawia żadnych wymagoń co do liczebności obserwacji.

ALGORYTM ANALIZY KORESPONDENCJI

1. Konstrukcja macierzy danych wejściowych:

; j=1,2,...,m; i=1,2,....n.

gdzie:

x_ji - wartość j-tej zmiennej w i-tym obiekcie.

wiersze macierzy X mogą być interpretowane w ujęciu geometrycznym jako współrzędne punktów zmiennych w n-wymiarowej przestrzeni obiektów Rn

kolumny macierzy X mogą być interpretowane jako współrzędne punktów - obiektów w m-wymiarowej przestrzeni zmiennych Rm

w podejściu klasycznym macierzą danych wejściowych jest dwuwymiarowa tablica kontyngencji
, której elementami są liczebności jednostek obserwacji posiadające jednocześnie j-tą kategorię pierwszej z charakteryzujących je zmiennych i i-tą kategorię drugiej ze zmiennych

2. Przekształcenie macierzy obserwacji X w macierz częstości względnych

, j=1,2,...,m; i=1,2,....n.

gdzie:

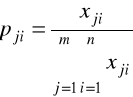
następuje zmiana skali wartości zmiennych poprzez ich unormowanie w przedziale [0;1]

3. Przekształcenie macierzy częstości P w macierze profili

1. Konstrukcja macierzy profili wierszy o postaci

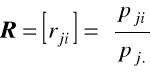
, j=1,2,...,m; i=1,2,....n.

gdzie:

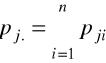
• elementy profili wierszowych mogą być traktowane jako współrzędne wektorów wierszowych (zmiennych w nieklasycznej analizie korespondencji) w n-wymiarowej przestrzeni euklidesowej Rⁿ.

2. Konstrukcja macierzy profili kolumn o postaci

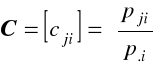
, j=1,2,...,m; i=1,2,....n.

gdzie:

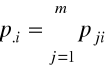
• elementy profili kolumnowych są współrzędnymi wektorów kolumnowych (obiektów w nieklasycznej analizie korespondencji) w m-wymiarowej przestrzeni euklidesowej R^m.

• częstości brzegowe, odpowiednio wierszy (r) i kolumn (c), w macierzach profili R i C są odpowiednio średnimi profilami kolumnowymi i wierszowymi (centrum kolumnowowym albo wierszowym). Punkty reprezentowane przez przeciętne profile wierszowe i kolumnowe nazywane są centroidami i leżą w środku układu współrzędnych.

• odległości pomiędzy profilami wierszowymi (punktami reprezentującymi kategorie pierwszej ze zmiennych) w przestrzeni Rⁿ wylicza się za pomocą ważonej metryki euklidesowej, gdzie wagami są częstości brzegowe kolumn, o postaci:

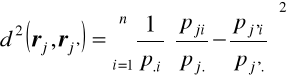
, j,j'=1,2,...,m; j≠j'.

• odległości pomiędzy profilami kolumnowymi (punktami reprezentującymi kategorie drugiej ze zmiennych w przestrzeni R^m) określamy za pomocą metryki euklidesowej, gdzie wagami są częstości brzegowe wierszy:

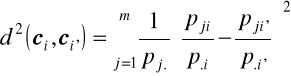
, i,i'=1,2,...,n; i≠i'.

• powyższe odległości są jednocześnie odległościami χ².

• analiza odległości pomiędzy profilami wierszowymi (kolumnowymi) jest tożsama z analizą odległości profili wierszowych (kolumnowych) od średnich profili wierszowych (kolumnowych)

INERCJA

• inercja jest miarą zróżnicowania elementów w macierzy danych wejściowych

• całkowita inercja macierzy określa stopień dyspersji profili wierszowych (kolumnowych) względem odpowiadających im centroid, czyli wskazuje jak bardzo poszczególne profile wierszowe (kolumnowe) różnią się od odpowiadającego im średniego profilu

• inercja dla wierszy obliczana jest według formuły średniej ważonej:

,

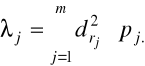
gdzie:

- odległość χ² między j-tym wierszem, a odpowiadającą jemu centroidą.

• inercję dla kolumn szacujemy w oarciu o wzór:

,

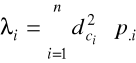
gdzie:

- odległość χ² między i-tą kolumną, a odpowiadającą jej centroidą.

• inercja dla wierszy jest równa inercji dla kolumn i jednocześnie równa inercji całkowitej:

.

• inercja posiada też interpretację geometryczną jako miara rozproszenia punktów reprezentujących profile w wielowymiarowej przestrzeni

• wartość inercji równa jest zero gdy punkty reprezentujące profile wierszowe (kolumnowe) skupiają się w początku układu współrzędnych. Odpowiada to sytuacji, że wszystkie profile wierszowe (kolumnowe) są takie same

• czym większa wartość inercji tym większe rozproszenie punktów reprezentujących profile w stosunku do środka układu współrzędnych

• maksymalna wartość całkowitej inercji jest równa s=min (m-1, n-1)

4. Symetryczna standaryzacja macierzy P

, j=1,2,...,m; i=1,2,....n,

gdzie:

.

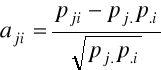
• przekształcenie umożliwia znalezienie przestrzeni czynnikowej (wektorów kierunkowych osi czynnikowych) na bazie n-punktów (obiektów w nieklasycznej analizie korespondencji) w przestrzeni m-wymiarowej (analiza względem kolumn macierzy A) lub też na podstawie m-punktów (zmiennych w nieklasycznej analizie korespondencji) w przestrzeni n-wymiarowej (analiza względem wierszy macierzy A)

• symetryczna standaryzacja wejściowej macierzy danych pozwala nie tylko na ustalenie struktury czynnikowej zmiennych oraz położenia obiektów w nowym czynnikowym układzie odniesienia, podobnie jak ma to miejsce w pozostałych metodach czynnikowych, ale także na ustalenie struktury czynnikowej obiektów oraz położenia zmiennych w tym samym układzie odniesienia, co nie jest możliwe w żadnej innej metodzie czynnikowej

5. Umieszczenie w nowym ortogonalnym układzie odniesienia (przestrzeni czynnikowej) rozpatrywanej konfiguracji punktów - obiektów oraz konfiguracji punktów zmiennych

• szukamy wspólnego, ortogonalnego układu odniesienia (podprzestrzeni o wymiarze min(m-1,n-1)) dla punktów reprezentujących profile wierszowe i profile kolumnowe.

• należy znaleźć wektory czynnikowe kolejnych osi czynnikowych przechodzących przez początek układu współrzędnych (zawierających centroidy), które najlepiej, w sensie maksymalizacji sumy kwadratów rzutów wektorów a_i(a_j) na te osie, dopasowują konfigurację n-punktów (m-punktów) umieszczonych w przestrzeni R^m(Rⁿ)

• wektory osi czynnikowej są szukane analogicznie jak miało to miejsce w analizie głównych składowych z tym, że odpowiednikiem macierzy korelacji R jest macierz A^TA(AA^T)

• należy znaleźć wartości własne macierzy A^TA(AA^T) i odpowiadające im wektory własne. Rząd macierzy A^TA jest, przy tym równy rzędowi macierzy AA^T, a także macierzy A

• kolejne osie czynnikowe, podobnie jak w analizie głównych składowych, szukane są w taki sposób aby odpowiadające im wymiary wyjaśniały jak największą część całkowitej inercji

Metoda rozkładu macierzy A według wartości osobistych

,

gdzie:

U^TU=V^TV=I

przy czym:

- macierz (m x s) składającą się z wektorów osobliwych odpowiadających pierwiastokom kwadratowym wartości własnych macierzy A^TA,

=[diag(λ_l)] - macierz diagonalną (s x s) utworzoną z niezerowych wartości własnych macierzy AA^T oraz A^TA, uporządkowanych malejąco,

V= [Vu_li] - macierz (s x n) składającą się z wektorów osobliwych odpowiadających pierwiatkom kwadratowym wartości własnych macierzy AA^T.

Wartości osobliwe macierzy A są pierwiastkami kwadratowymi wartości własnych macierzy A^TA oraz AA^T.

,

gdzie:

Γ - jest macierzą diagonalną (s x s) utworzoną z niezerowych wartości własnych γ_l(l=1,2,...,s) uporządkowanych malejąco.

• wektory u₁,u₂,...,u_s macierzy U nazywane są lewymi wektorami osobliwymi i tworzą ortonormalną bazę dla kolumn macierzy A (stanowią tzw. osie główne podprzestrzeni czynnikowej rzutowania kategorii zapisanych w kolumnach w ujęciu klasycznym, czy też obiektów w ujęciu nieklasycznym)

• wektory v₁,v₂,...,v_s macierzy V nazywane są prawymi wektorami osobliwymi i tworzą ortonormalną bazę dla transponowanych wierszy macierzy A (stanowią tzw. osie główne podprzestrzeni czynnikowej rzutowania kategorii zapisanych w wierszu w ujęciu klasycznym, czy też zmiennych w ujęciu nieklasycznym)

• podprzestrzenie te nakładamy na siebie tak aby układy współrzędnych czynnikowych pokryły się

• współrzędne czynnikowe pierwszej z kategorii zmiennych (zmiennych w nieklasycznej analizie korespondencji), zapisanych w wierszach macierzy kontyngencji, są uzyskiwane w oparciu o równanie:

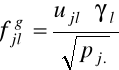
, j=1,2,...,m; l=1,2,....s,

gdzie:

- l-ta wartość osobliwa.

• współrzędne czynnikowe drugiej z kategorii zmiennych (obiektów w nieklasycznej analizie korespondencji), podane w kolumnach macierzy kontyngencji obliczane są one na podstawie równania:

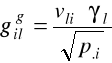
, i=1,2,...,n; l=1,2,....s.

WYBÓR PRZESTRZENI CZYNNIKOWEJ

• gdy odtwarzamy odległości pomiędzy punktami reprezentującymi kategorie danej zmiennej (punkty reprezentujące obiekty albo zmienne w nieklasycznej analizie korespondencji) w przestrzeni o maksymalnym wymiarze s=min(m-1; n-1) odtwarzamy pierwotne konfiguracje punktów bez żadnych zniekształceń, tzn. zostają zachowane kąty między wektorami i odległości wektorów reprezentujące profile wierszowe (kolumnowe), a co za tym idzie również odległości między punktami

• każde zmniejszenie maksymalnego wymiaru przestrzeni czynnikowej powoduje zniekształcenie konfiguracji wyjściowej punktów co oznacza stratę informacji o badanym zjawisku

• ostatecznie wybrany wymiar przestrzeni czynnikowej, w której przeprowadzono analizę uzyskanych wyników, jest kompromisem między łatwością ich interpretacji, przede wszystkim w ujęciu graficznym, a stopniem odtworzenia pierwotnej informacji o badanym zjawisku w tym wymiarze

• przy podejmowaniu decyzji co do optymalnego wymiaru przestrzeni czynnikowej możemy korzystać przede wszystkim z kryterium osypiska kryterium, liczby zmiennych oraz stopnia wyjaśniania inercji

JAKOŚĆ ODWZOROWANIA

• jakość odwzorowania poszczególnych punktów (wierszy lub kolumn) w danym wymiarze przestrzeni czynnikowej mierzona jest poprzez stosunek kwadratu odległości danego punktu w tym wymiarze od środka układu osi czynnikowych maksymalnego wymiaru do kwadratu odległości tego punktu w przestrzeni czynnikowej o maksymalnym wymiarze od środka układu czynnikowego

• stosunek ten jest tożsamy ze stosunkiem udziału danego wymiaru w inercji punktu (kwadrat korelacji wektorów wierszowych (kolumnowych) z daną osią czynnikową, czyli określa jaka część inercji punktu jest wyjaśniana przez dany wymiar.

• jakość odwzorcowania dla punktów reprezentujących wiersze (zmienne) jest obliczana na podstawie wzoru:

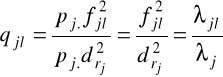
, j=1,2,...,m; l=1,2,....s,

gdzie:

q_jl - jakość odwzorcowania j-tego punktu przez l-ty wymiar,

- inercja j-tego punktu w l-tym wymiarze.

• jakość odwzorowania dla punktów reprezentujących kolumny (obiekty) wzór ten przyjmuje postać:

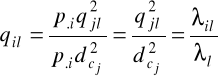
, i=1,2,...,n; l=1,2,....s,

gdzie:

q_il - jakość odwzorcowania i-tego punktu przez l-ty wymiar,

- inercja i-tego punktu w l-tym wymiarze.

• suma wartości jakości odwzorcowania danego punktu po wszystkich wymiarach przestrzeni czynnikowej równa jest jeden

• jakość odwzorcowania danego punktu w wybranej podprzestrzeni czynnikowej o wymiarze mniejszym od wymiaru maksymalnego jest sumą jakości odwzorcowania tego punktu, w kolejnych wymiarach i oceniana dla punktów wybranej podprzestrzeni reprezentujących wiersze na podstawie formuły:

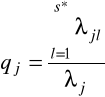
, j=1,2,...,m; s*≤s

• jakości odwzorowania dla punktów reprezentujących kolumny obliczana jest w oparciu o formułę:

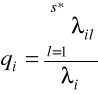
, i=1,2,...,n; s*≤s

ZNACZENIE PUNKTÓW W TWORZENIU

PRZESTRZENI CZYNNIKOWEJ

• znaczenie poszczególnych punktów (reprezentujących kategorie zmiennych w podejściu klasycznym albo obiekty i zmienne w podejściu nieklasycznym) w tworzeniu poszczególnych wymiarów przestrzeni czynnikowej jest mierzone udziałem punktów w inercji (bezwładności) tych wymiarów

• suma tych udziałów dla wszystkich punktów łącznie jest dla każdego z wymiarów przestrzeni czynnikowej równa jedności

• udział punktu reprezentującego wiersz w danym wymiarze obliczana jest w oparciu o wzór:

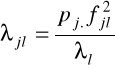
, j=1,2,...,m; l=1,2,....s.

• udział punktu reprezentującego kolumnę określa wzór:

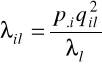
, i=1,2,...,n; l=1,2,....s.

• znaczenie poszczególnych punktów w tworzeniu całej przestrzeni czynnikowej (wielkość zasobów informacyjnych o badanym zjawisku poszczególnych kategorii zmiennych w ujęciu klasycznym albo obiektów lub zmiennych w ujęciu nieklasycznym) oceniane jest na podstawie formuł:

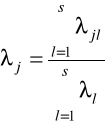
, j=1,2,...,m,

oraz

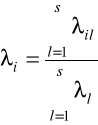
, i=1,2,...,n.

Punkty dodatkowe

• punkty te zawierają dodatkową informację o badanym zjawisku. Punkt dodatkowy może:

• odzwierciedlać sumę kategorii jednej ze zmiennych (w ujęciu nieklasycznym może to być przykładowo suma wystandaryzowanych wartości pewnej grupy rozważanych zmiennych dla poszczególnych obiektów)

• stanowić dodatkową kategorię jednej z zmiennych (w ujęciu nieklasycznym na przykład dodatkową własność badanych obiektów)

• reprezentować kategorię jednej z zmiennych tak znacznie odstającą od innych kategorii, że włączenie go do głównej analizy spowoduje zgrupowanie wszystkich innych punktów reprezentujących pozostałe kategorie analizowanych zmiennych wokół środka układu współrzędnych czynnikowych, co znacznie utrudni analizę wyników

• współrzędne dodatkowego punktu opisywanego przez wiersze są wyznaczane w oparciu o formułę:

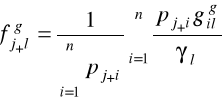
, j₊=1,2,...,m₊; l=1,2,....s.

• współrzędne dodatkowego punktu opisywanego przez kolumnę są szacowane w oparciu o formułę:

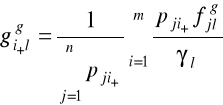
, i₊=1,2,...,n₊; l=1,2,....s.

INTERPRETACJA OSI CZYNNIKOWYCH

• nazwy nadawane są poszczególnym osiom czynnikowym na podstawie oceny siły ich skorelowania z punktami reprezentującymi kategorie badanych zmiennych, podobnie jak w innych metodach czynnikowych

• nazwa osi czynnikowej związana jest z tymi kategoriami zmiennych (zmiennym oraz obiektami w ujęciu nieklasycznym), dla których korelacji z tą osią są najsilniejsze

Podejścia interpretacyjne:

• zaleca się aby nazwa osi była ustalana w oparciu o analizę jej korelacji z kategoriami tej samej zmiennej (w ujęciu nieklasycznym na bazie analizy korelacji osi ze zmiennymi albo z obiektami)

• drugim nazwę osi ustala przez badanie korelacji z kategoriami obu zmiennych. Ponadto korelacje te są badane oddzielnie dla półosi dodatnich i półosi ujemnych.

INTERPRETACJA WYNIKÓW

• w formie tablic, w których zawarte są współrzędne poszczególnych zmiennych (obiektów) względem kolejnych osi czynnikowych

• w formie graficznej w postaci wykresów sporządzonych na podstawie tych tablic, będących dwumiarowymi przekrojami przestrzeni czynnikowych

TYPY KONFIGURACJI PUNKTÓW PODLEGAJĄCYCH ANALIZIE

• położenie punktów względem środka układu współrzędnych (centrum rzutowania)

• położenie względem siebie punktów odpowiadającym kategoriom tej samej zmiennej (obiektom albo zmiennym w podejściu nieklasycznym)

• położenie względem siebie punktów odpowiadającym kategoriom różnych zmiennych (położenie punktów reprezentujących obiekty względem punktów reprezentujących zmienne i vice versa)

ANALIZA PUNKTÓW

WZGLĘDEM ŚRODKA UKŁADU WSPÓŁRZĘDNYCH

• punkty położone, w porównaniu z innymi punktami, blisko początku czynnikowego układu odniesienia (reprezentującego profil przeciętny) posiadają profile bliskie profilowi przeciętnemu, a położenie relatywnie daleko mają profile znacznie różniące się od profilu przeciętnego

• czym punkty są położone dalej od początku układu odniesienia tym mają większy wkład w tworzenie przestrzeni czynnikowej (większe zasoby informacyjne o badanym zjawisku).

• w ujęciu nieklasycznym analiza położenia punktów zmiennych względem początku czynnikowego układu odniesienia wskazuje na stopień ich zróżnicowania w badanych obiektach na tle pozostałych rozpatrywanych zmiennych

• małe oddalenie od początku układu punktu-zmiennej świadczy o niewielkim zróżnicowaniu tej zmiennej w badanych obiektach w porównaniu ze zróżnicowaniem innych zmiennych

• duża odległość punktu-zmiennej od początku układu czynnikowego wskazuje na jej silne zróżnicowanie w badanych obiektach w porównaniu z innymi zmiennymi.

• analiza odległości punktu obiektu, w ujęciu nieklasycznym, od początku układu czynnikowego, będącą wypadkową odległości pomiędzy odpowiadającymi sobie zmiennymi w danym obiekcie i w obiekcie przeciętnym (centroidzie), pozwala na ocenę relatywnego (w stosunku do innych obiektów), stopnia nietypowości danego obiektu ze względu na strukturę opisujących go zmiennych

POŁOŻENIE WZGLĘDEM SIEBIE PUNKTÓW ODPOWIADAJĄCYM KATEGORIOM TEJ SAMEJ ZMIENNEJ (OBIEKTOM ALBO ZMIENNYM

W PODEJŚCIU NIEKLASYCZNYM)

• czym bliższe położenie punktów reprezentujących kategorie tej samej zmiennej, tym ich profile są bardziej podobne

• w ujęciu nieklasycznym

• bliskie położenie punktów zmiennych w przestrzeni czynnikowej oznacza, że zmienne te kształtują się podobnie w badanych obiektach

• bliskie położenie punktów reprezentujących obiekty wskazuje na podobieństwo struktury opisujących je zmiennych

POŁOŻENIE WZGLĘDEM SIEBIE PUNKTÓW ODPOWIADAJĄCYM KATEGORIOM RÓŻNYCH ZMIENNYCH (POŁOŻENIE PUNKTÓW REPREZENTUJĄCYCH OBIEKTY WZGLĘDEM PUNKTÓW REPREZENTUJĄCYCH ZMIENNE I VICE VERSA)

• można interpretować położenie punktu reprezentującego kategorię jednej ze zmiennych w odniesieniu do konfiguracji punktów reprezentujących wszystkie kategorie drugiej ze zmiennych (w ujęciu nieklasycznym położenie punktu zmiennej względem konfiguracji punktów obiektów lub położenie punktu obiektu względem konfiguracji punktów zmiennych)

• bliskie położenie punktów reprezentujących kategorie różnych zmiennych wskazuje na ich współwystępowanie

• w ujęciu nieklasycznym, przykładowo bliskie położenie punktów zmiennych w stosunku do danego punktu obiektu wskazuje, że właśnie ze względu na wartości zmiennych reprezentowanych przez te punkty dany obiekt wyróżnia się od innych badanych obiektów

---