Wydział Inżynierii i Technologii Chemicznej |
Imię i Nazwisko: |
Zespół: 3 |
Ocena: |
Grupa: 14 |
Tytuł ćwiczenia: |
Nr ćw.: 27 |
Data wykonania: |
Dyfrakcja i interferencja światła lasera na szczelinach
Wprowadzenie
Dyfrakcja i interferencja fal świetlnych
Fale świetlne, to fale elektromagnetyczne o długościach z przedziału 400 nm do 760 nm, polegające na rozchodzeniu się w przestrzeni periodycznie zmiennego w czasie pola elektrycznego i związanego z nim pola magnetycznego. W zjawiskach optycznych decydującą rolę odgrywa wektor natężenia pola elektrycznego E (zwany też wektorem świetlnym), który dla monochromatycznej fali płaskiej dany jest wzorem: ![]()
.
gdzie: k jest wektorem falowym o kierunku propagacji fali (k = 2Π / λ), r to wektor położenia, ω - częstość kołowa, a ф - faza początkowa. Z falową naturą światła związane są zjawiska dyfrakcji i interferencji.
Zjawisko polegające na uginaniu się promieni świetlnych padających na przeszkody lub przechodzących przez szczeliny nazywamy dyfrakcją. Efekty dyfrakcyjne są silne wówczas, gdy rozmiary obiektów znajdujących się na drodze fali świetlnej są porównywalne z jej długością λ. Jeśli za wąską szczeliną o szerokości a, na którą pada fala świetlna o długości λ umieścimy ekran w odległości L >> a, to będziemy na nim obserwować układ jasnych i ciemnych prążków o zmieniającym się natężeniu. Powstawanie takiego obrazu dyfrakcyjnego możemy wytłumaczyć na podstawie zasady Huyghensa i zjawiska interferencji. Położenia ciemnych prążków, czyli minimów natężenia światła, dane są warunkiem: a sin αn = nλ,
gdzie: n jest liczbą całkowitą, a - szerokością szczeliny.
Dla pierwszego minimum, gdy n = 1 mamy: sin α1 = λ / a.
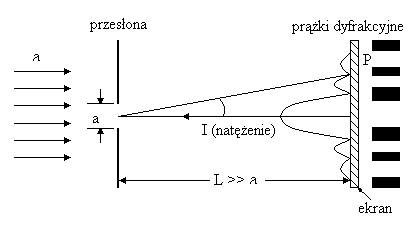
Z zależności tej widać, że obraz dyfrakcyjny światła na jednej szczelinie zależy od stosunku λ / a. Zmieniając szerokość szczeliny możemy zmieniać położenie pierwszego ciemnego prążka. Dla bardzo wąskich szczelin, dla których spełniony jest warunek λ > a, nie istnieje taki kąt α1, dla którego mogłoby nastąpić wygaszenie w wyniku zjawiska dyfrakcji i fala ugięta na szczelinie oświetla centralną część ekranu w sposób równomierny.
Zjawisko dyfrakcji można łatwo zaobserwować w przypadku użycia w doświadczeniu wiązki światła laserowego. jest ono bowiem w wysokim stopniu monochromatyczne i skolimowane, w przeciwieństwie do źródeł konwencjonalnych (np. lampy) i nie zachodzi zacieranie się obrazu dyfrakcyjnego poprzez nakładanie się na siebie obrazów dyfrakcyjnych różnych długości fal czy też wytworzonych przez odległe punkty powierzchni źródła.
Interferencja fal polega na nakładaniu się dwu lub więcej fal harmonicznych o tej samej długości, prowadzącym do powstania ustalonego w czasie przestrzennego rozkładu obszarów wzmocnienia i osłabienia fali wypadkowej. Zjawisko to możemy obserwować, gdy światło pada na dwie szczeliny. jeśli długość fali świetlnej λ jest większa od szerokości każdej ze szczelin (zgodnie z tym, co zostało wykazane, w przypadku, gdy λ > a fala ugięta na pojedynczej szczelinie oświetla ekran w sposób niemal równomierny), to przechodzące przez nie i ugięte fale dają obraz interferencyjny składający się na przemian jasnych i ciemnych prążków o prawie jednakowym natężeniu. W określonym punkcie P ekranu obserwujemy prążek jasny, jeśli dociera do niego równocześnie maksimum (lub minimum) pierwszej i drugiej fali. Wówczas bowiem zachodzi sumowanie się amplitud fal wypadkowych. W przypadku, gdy w rozważanym punkcie P spotyka się minimum jednej i maksimum drugiej fali, dochodzi do wygaszenia fal.
Dla sytuacji przedstawionej powyżej, gdzie r1 i r2 są odpowiednio odległościami szczelin S1 i S2 od punktu P na ekranie, a δ = r1 - r2 jest tu różnicą dróg optycznych, warunkiem wzmocnienia jest, by δ była całkowitą wielokrotnością długości fali λ. Przy założeniu, że odległość szczelin od ekranu L jest dużo większa niż odległość między szczelinami d (L >> d), różnica dróg optycznych δ wyraża się wzorem: δ = d sin α i ostatecznie z powyższych dostajemy, że jasne prążki interferencyjne (maksima w natężeniu światła) występują wówczas, gdy: d sin αn = n λ, gdzie n jest liczbą całkowitą.
Z kolei wygaszenia światła obserwujemy w tych punktach, dla których: δ = r1 - r2 = (2n - 1)λ/2
Zjawiska interferencji i dyfrakcji rzadko występują oddzielnie. Dla realnych szczelin, których szerokości są większe lub porównywalne z długością fali świetlnej natężenie uzyskanego obrazu interferencyjnego będzie modulowane przez czynnik dyfrakcyjny. Uzyskane prążki interferencyjne będą miały wyraźnie zmieniające się natężenie zależne od obrazu dyfrakcyjnego od obrazu dyfrakcyjnego od pojedynczej szczeliny.
Omawiając zjawisko interferencji rozpatrywaliśmy wyidealizowane fale monochromatyczne. W rzeczywistości światło wysyłane przez konwencjonalne źródła światła jest skomplikowaną superpozycją skończonych ciągów fal o różnych długościach, emitowanych przez atomy w sposób zupełnie przypadkowy. To sprawia, że przy nakładaniu się fal na siebie położenia obszarów wzmocnień i osłabień ulegają ciągłym zmianom i nie jest możliwe obserwowanie interferencji wiązek światła wysyłanych przez różne źródła. Mówimy, że są one wiązkami niespójnymi. Wyraźny stabilny w czasie obraz interferencyjny możemy uzyskać tylko wtedy, gdy różnice faz między nakładającymi się falami są stałe w czasie obserwacji. Fale takie nazywamy spójnymi i źródłem ich są lasery.
Zasada działania lasera
Lasery są źródłami spójnego, monochromatycznego i w wysokim stopniu skolimowanego światła. Wiązka promieniowania laserowego powstaje w wyniku zjawiska emisji wymuszonej promieniowania po poprzednim wytworzeniu w ośrodku czynnym stanu inwersji obsadzeń, polegającego na zwiększeniu liczby atomów wzbudzonych tak , by przewyższała liczbę atomów w stanie niższym. Proces ten określa się mianem pompowania.
Zależnie od materiału użytego jako ciało aktywne, dzielimy lasery na: krystaliczne (rubinowy, neodymowy), gazowe (helowo-neonowy), lasery barwnikowe (roztwory silnie fluoryzującego barwnika, np. rodaminy) i półprzewodnikowe.
Zasada działania lasera półprzewodnikowego
Lasery półprzewodnikowe, to odpowiednio sporządzone diody półprzewodnikowe, których zasadniczym elementem jest złącze p-n. poprzez wstrzykiwanie nośników ładunku do obszaru złącza uzyskuje się inwersję obsadzeń, zaś rekombinacji elektronów i dziur w tym obszarze towarzyszy emisja fotonów. W laserze emisja wymuszona dominuje na spontaniczną i diodę opuszcza monochromatyczne, spolaryzowane światło spójne.
Metoda wyznaczania szerokości szczeliny a z obserwacji dyfrakcji światła na pojedynczej szczelinie.
W doświadczeniu z dyfrakcją światła na jednej szczelinie oznaczmy odległość szczeliny od ekranu przez L, a odległość punktu P na ekranie od środka ekranu O przez y. Jeśli spełniony jest warunek, że L >> a, to wówczas możemy różnicę dróg optycznych δ dla promieni1 i 2 zapisać jako:
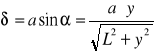
Z powyższej zależności oraz ze wzoru asin αn = n λ wynika, że położenie minimów natężenia światła (ciemnych prążków) na ekranie, yn, gdy λ < a dane jest równaniem:
![]()
gdzie n jest liczbą całkowitą.
Dla y= 0 mamy bardzo wyraźne maksimum środkowe w rozkładzie natężenia światła. Znając położenie n-tego minimum możemy z powyższego wzoru wyznaczyć szerokość szczeliny a:
![]()
Metoda wyznaczania stałej siatki dyfrakcyjnej
Warunkiem wystąpienia prążków jasnych w doświadczeniu z siatką dyfrakcyjną jest spełnienie zależności:
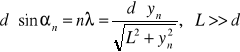
gdzie: n jest rzędem widma, d - stałą siatki, L - odległością ekranu od siatki dyfrakcyjnej, yn - odległością jasnego prążka n-tego rzędu od środka obrazu, czyli od jasnego prążka rzędu zerowego. Z powyższego wzoru można wyznaczyć stałą siatki d:
![]()
Opracowanie wyników
L = 113 cm λ = 670 nm |
||
nr pomiaru |
y [mm] |
U [V] |
1 |
-17 |
0,1900 |
2 |
-16 |
0,1600 |
3 |
-15 |
0,1800 |
4 |
-14 |
0,2500 |
5 |
-13 |
0,2700 |
6 |
-12 |
0,2300 |
7 |
-11 |
0,3500 |
8 |
-10 |
0,5500 |
9 |
-9 |
0,5600 |
10 |
-8 |
0,4700 |
11 |
-7 |
0,9600 |
13 |
-6 |
1,580 |
14 |
-5 |
1,610 |
15 |
-4 |
1,850 |
16 |
-3 |
8,000 |
17 |
-2 |
21,80 |
18 |
-1 |
40,22 |
19 |
0 |
48,54 |
20 |
1 |
43,32 |
21 |
2 |
23,31 |
22 |
3 |
9,420 |
23 |
4 |
2,770 |
24 |
5 |
1,580 |
25 |
6 |
1,720 |
26 |
7 |
1,040 |
27 |
8 |
0,5300 |
28 |
9 |
0,5600 |
29 |
10 |
0,6100 |
30 |
11 |
0,3600 |
31 |
12 |
0,2400 |
32 |
13 |
0,2700 |
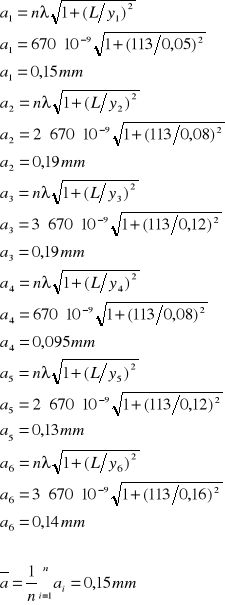
Nr minimum - n |
yn [mm] |
an [mm] |
1 |
5 |
0,15 |
2 |
8 |
0,19 |
3 |
12 |
0,19 |
4 |
-8 |
0,095 |
5 |
-12 |
0,13 |
6 |
-16 |
0,14 |
ā = 0,15 mm |
||
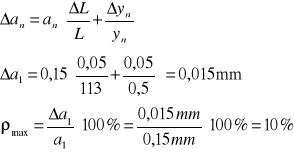
L = 113 cm λ = 670 nm |
||
nr pomiaru |
y [mm] |
U [V] |
1 |
-30 |
0,1000 |
2 |
-20 |
0,5700 |
3 |
-10 |
6,460 |
4 |
0 |
80,05 |
5 |
10 |
5,850 |
6 |
20 |
0,3200 |
7 |
30 |
0,09000 |
Nr maksimum - n |
yn [mm] |
dn [mm] |
1 |
30 |
0,076 |
2 |
20 |
0,076 |
3 |
10 |
0,075 |
4 |
-10 |
0,076 |
5 |
-20 |
0,076 |
6 |
-30 |
0,075 |
ā = 0,076 mm |
||
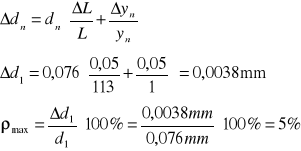
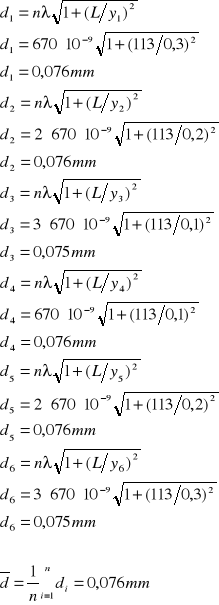
Wyszukiwarka
Podobne podstrony:
LAB1, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 001 WA~1
25OPR, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 025 IN~1
LAB01, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 001 WA~1
LAB22TAB, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 022 ST~1
LAB25 , Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 025 IN~1
fale, Fizyka laborki, Fizyka (laby i inne)
WYKLADY, Fizyka laborki, Fizyka (laby i inne)
WYKLADY, Fizyka laborki, Fizyka (laby i inne)
LAB25!, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 025 IN~1
WYKLADY, Fizyka laborki, Fizyka (laby i inne)
Kinematyka, Fizyka laborki, Fizyka (laby i inne)
LAB13 , Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 013 LE~1
więcej podobnych podstron