WEAiIE |
Biegański Marek Madej Marek |
Grupa I |
Zespół 11 |
|||
Laboratorium Fizyczne |
Temat: Interferencja fal akustycznych |
Nr ćwiczenia: 25 |
||||
Data wykonania: 4.03.1999 |
Data oddania:
11.03.1999 |
Zwrot do poprawy: 18.03.1999 |
Data odbioru:
25.03.1999 |
Data zaliczenia: |
Ocena: |
|
1. Cel ćwiczenia
Celem ćwiczenia jest doświadczalne wyznaczenie prędkości dźwięku w powietrzu metodą interferencji fal akustycznych, przy użyciu rury Quinckego.
2. Wprowadzenie teoretyczne
Proces rozchodzenia się drgań w przestrzeni nazywa się falą. Cząstki ośrodka, w którym fala rozchodzi się, nie są wciągane przez falę do ruchu postępowego, wykonują jedynie drgania wokół swoich położeń równowagi. W zależności od kierunku drgań cząstek w odniesieniu do kierunku rozchodzenia się fali rozróżnia się fale podłużne i poprzeczne. W ośrodkach ciekłych i gazowych możliwe jest tylko rozchodzenie się fal podłużnych.
Jeżeli fale sprężyste, rozchodzące się w powietrzu, mają częstotliwość przypadającą na przedział od 16 do 20000 Hz, to dosięgając ucha ludzkiego wywołują wrażenie dźwięku. W związku z tym fale sprężyste, rozchodzące się w dowolnym ośrodku i charakteryzujące się częstotliwościami przypadającymi na wyżej wymieniony przedział, nazywa się falami akustycznymi lub po prostu dźwiękami.
Prędkość fali można wyznaczyć ze wzoru:
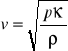
gdzie:
ρ - gęstość ośrodka,
p - ciśnienie,
κ - stosunek ciepeł właściwych cp/cv.
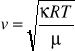
Wykorzystując wzór Clapeyrona można wzór doprowadzić do postaci:
gdzie:
R - uniwersalna stała gazowa,
T - temperatura bezwzględna,
μ - ciężar cząsteczkowy.
Ponieważ wykorzystywanie tego wzoru w praktyce jest trudne, dlatego aby wyznaczyć tę wielkość skorzystamy ze zjawiska interferencji fal dźwiękowych. Zjawisko to polega na nakładaniu się dwóch lub większej ilości fal. W wyniku interferencji fale mogą się wzmacniać (jeżeli ich fazy są zgodne) lub wygaszać (jeżeli ich fazy są przeciwne). Ilościowo interferencję można policzyć korzystając z zasady superpozycji.
Zasada superpozycji dwóch fal
Rozpatrzmy superpozycję dwóch fal, które wyszły z tego samego źródła i do pewnego punktu ośrodka docierają dwiema różnymi drogami długości x1 i x2. Amplitudy fal są równe odpowiednio:
y1 = ymax sin ( kx1 - ω t )
y2 = ymax sin ( kx2 - ω t )
a amplituda wypadkowa:
yw = y1 + y2
Po przekształceniach otrzymujemy wzór:
![]()
gdzie ϕ jest funkcją x1, x2 oraz długością fali λ.
Pierwszy czynnik tego iloczynu daje amplitudę drgania wypadkowego w rozważanym punkcie. Czynnik ten osiąga wartość minimalną, gdy:
cos k(x1 - x2) = - 1.
Ma to miejsce, wtedy, gdy x1 - x2 = λ (n - 0,5), to znaczy gdy różnica dróg, po których biegną fale jest równa nieparzystej wielokrotności połówek długości fali. Pierwsze minimum otrzymujemy dla n = 1, wtedy
x1 -x2 = 0,5 λ; drugie zaś dla n=2, wtedy x1 -x2 = 1,5 λ; itd. Odległość między kolejnymi minimami jest równa długości fali: 1,5 λ - 0,5 λ = λ; 2,5 λ - 1,5 λ = λ; itd.
W doświadczeniu użyto rury Quinckego. Są to dwie zgięte równoległe do siebie rury, z których jedna ma długość niezmienną, drugą można skracać lub wydłużać. Urz --> [Author:brak] ądzenie to rozdziela fale na dwie części, które biegnąc po różnych drogach spotykają się i interferują ze sobą. Mierząc odległość między kolejnymi minimami, która odpowiada połowie długości fali dźwiękowej (faktyczna zmiana długości rury jest dwa razy większa od wartości odczytanej na skali, gdyż przesuwają się dwa „ramiona” rury, każde o taką samą odległość), jesteśmy w stanie obliczyć prędkość fali stosując następującą zależność:
v = f λ
3. Wyniki pomiarów i ich opracowanie
Częstotliwo ść [Hz] |
Położenie kolejnych minimów [cm]
|
Różnica położeń kolejnych minimów [cm]
|
Długość fali [cm] |
Pręd kość dźwię ku [m/s] |
|||||||||||||
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
Δa1 |
Δa2 |
Δa3 |
Δa4 |
Δa5 |
Δa6 |
Δa7 |
λśr |
v |
670 |
11,2 |
36,1 |
|
|
|
|
|
|
24,9 |
|
|
|
|
|
|
49,8 |
333,7 |
750 |
9,8 |
32,5 |
|
|
|
|
|
|
22,7 |
|
|
|
|
|
|
45,4 |
341,3 |
800 |
8,1 |
28,6 |
|
|
|
|
|
|
20,5 |
|
|
|
|
|
|
41,0 |
328,0 |
900 |
7,3 |
26,3 |
|
|
|
|
|
|
19,0 |
|
|
|
|
|
|
38,0 |
342,0 |
950 |
7,2 |
25,2 |
43,2 |
|
|
|
|
|
18,0 |
18,0 |
|
|
|
|
|
36,0 |
342,0 |
1100 |
6,8 |
22,6 |
38,4 |
|
|
|
|
|
15,8 |
15,8 |
|
|
|
|
|
31,6 |
347,6 |
1400 |
8 |
20,5 |
33 |
|
|
|
|
|
12,5 |
12,5 |
|
|
|
|
|
25,0 |
350,0 |
2000 |
5,5 |
14 |
23,5 |
32 |
40,5 |
|
|
|
8,5 |
9,5 |
8,5 |
8,5 |
|
|
|
17,5 |
350,0 |
3000 |
2,7 |
8,4 |
13,9 |
19,5 |
25,1 |
30,6 |
36,3 |
41,9 |
5,7 |
5,5 |
5,6 |
5,6 |
5,5 |
5,7 |
5,6 |
5,6 |
336,0 |
3200 |
2,5 |
8 |
13 |
18,4 |
23,7 |
29 |
34,2 |
39,4 |
5,5 |
5 |
5,4 |
5,3 |
5,3 |
5,2 |
5,2 |
10,5 |
336,0 |
Prędkość wyliczono ze wzoru:
v = f λ
Prędkość średnia wynosi vśr = 340.6 m/s.
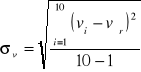
Błąd standardowy każdego pomiaru należy obliczyć ze wzoru:
Podstawiając dane do tego wzoru otrzymano wynik:
σv = 7,3 m/s
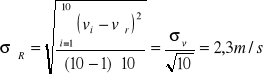
Błąd standardowy wartości średniej dany jest wzorem:
Tak więc ostatecznie prędkość dźwięku wyznaczona w doświadczeniu wynosi 340.6 m/s ± 2,3 m/s
Pomiary zostały wykonane przy temperaturze powietrza wynoszącej 24 °C = 297 K.
Wartość tablicowa prędkości dźwięku w temperaturze 0 °C wynosi 332 m/s.
By porównać otrzymany wynik z wartością tablicową należy skorzystać z następujących zależności:
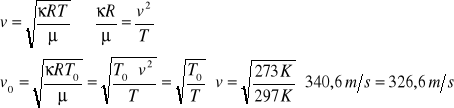
v0 - prędkość średnia sprowadzona do temperatury 0 °C.
Wartość v0 obarczona jest błędem:
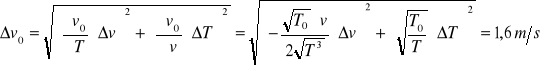
Czyli v0 = 326,6 m/s ±1,6 m/s
Błąd tablicowy wynosi zatem:
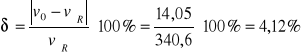
4. Wnioski
Błędy pomiarowe jakie mogły wyniknąć podczas naszych pomiarów możemy podzielić na:
1. Błędy wynikające z niedokładności przyrządów użytych podczas ćwiczenia
- błąd odczytu odległości który wyniósł 1m,
- błąd odczytu temperatury który wyniósł 1 °C,
- niedokładność ustawienia częstotliwości na skali przyrządu.
2. Błędy wynikające z niejednoznaczności odnalezienia położenia minimum natężenia dźwięku przez osobę przeprowadzającą pomiar (błąd ten możemy określić na około 0.5 cm).
Wszystkie te błędy powodują, że wykonany pomiar prędkości dźwięku różni się w pewnym stopniu od wartości tablicowej (którą odczytano z tablic fizycznych dla powietrza w temperaturze 0 °C).
W ćwiczeniu wykonano pomiary dla dźwięku o częstotliwości od 670 Hz do 3200 Hz. Okazało się, iż w miarę przechodzenia do wyższych częstotliwości zwiększała się ilość minimów. Potwierdził się także fakt, że prędkość dźwięku nie zależy od częstotliwości i wartość jaką otrzymano po wykonaniu obliczeń jest wartością zbliżoną do wartości tablicowej.
- 1 -
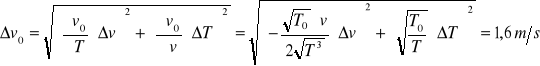
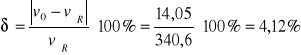
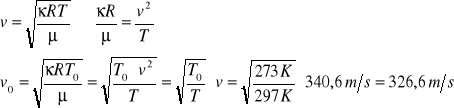
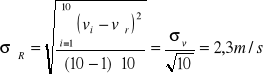
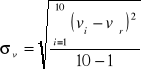
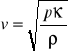
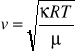
![]()
Wyszukiwarka
Podobne podstrony:
LAB25 , Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 025 IN~1
LAB25 ~1, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 025 IN~1
LAB1, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 001 WA~1
25OPR, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 025 IN~1
LAB01, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 001 WA~1
LAB22TAB, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 022 ST~1
LAB13 , Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 013 LE~1
LABTAB, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 002 WA~1
25WSTEP, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 025 IN~1
LAB02C, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 002 WA~1
LABOR2D, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 002 WA~1
FIZYKA~6, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 013 LE~1
LAB51, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 051
LABFIZ, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 013 LE~1
LAB22 , Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 022 ST~1
LAB1, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 001 WA~1
więcej podobnych podstron