WEAiIE |
Biegański Marek Madej Marek |
Grupa I |
Zespół 11 |
|||
Laboratorium Fizyczne |
Temat: Prawo Boyle'a - Mariotte'a i uniwersalna stała gazowa R |
Nr ćwiczenia: 22 |
||||
Data wykonania: 25.02.1999 |
Data oddania:
4.03.1999 |
Zwrot do poprawy: 11.03.1999 |
Data odbioru: |
Data zaliczenia: |
Ocena: |
|
1. Cel ćwiczenia
Zapoznanie się z układem próżniowym i pomiarem ciśnienia w tym układzie, sprawdzenie prawa Boyle'a - Mariotte'a dla powietrza w temperaturze pokojowej, wyznaczenie uniwersalnej stałej gazowej.
2. Wprowadzenie teoretyczne
Gaz doskonały
Gazem doskonałym w ujęciu teorii kinetyczno - molekularnej będziemy nazywali następujący uproszczony, wyidealizowany model gazu rzeczywistego:
a) gaz składa się z identycznych cząsteczek,
b) cząsteczki znajdują się w ciągłym ruchu i podlegają zasadom dynamiki Newtona,
c) całkowita liczba cząsteczek jest bardzo duża,
d) objętość i rozmiary liniowe cząsteczek są zaniedbywalnie małe,
e) cząsteczki nie oddziałują między sobą, za wyjątkiem samych zderzeń,
f) zderzenia są doskonale sprężyste i zachodzą w zaniedbywalnie krótkim czasie.
Równanie stanu gazu doskonałego dane jest wzorem:
pV = nRT
gdzie:
p - ciśnienie gazu;
V - objętość;
n - liczba moli gazu;
R - uniwersalna stała gazowa.
Prawo Boyle'a - Mariotte'a:
Opisuje przemianę izotermiczną (T = const) gazu doskonałego. Z równania stanu gazu doskonałego otrzymujemy:
pV = const = nRT, czyli p1V1 = p2V2
We współrzędnych p, V wykresem przemiany izotermicznej jest hiperbola.
Ciśnienie gazu wiąże się z oddziaływaniem cząsteczek z ściankami naczynia. Zderzając się z nimi wywierają nacisk. Jednostką ciśnienia w układzie SI jest paskal [Pa]. Jest to ciśnienie wywierające nacisk jednego niutona na jeden metr kwadratowy. Jednostkami pochodnymi są: atmosfera techniczna (1at = 0,9807e5 Pa), bar (1 bar = 1e5 Pa), milimetr słupa rtęci czyli tor (1 mm Hg = 1 Tr = 133,3 Pa), atmosfera fizyczna czyli normalna (1 At = 760 Tr = 1,01e5 Pa).
Próżnią nazywamy stan, jaki panuje w obszarze wypełnionym gazami lub parami, gdy ciśnienie jest niższe od ciśnienia atmosferycznego.
Próżnię wytwarza się w tzw. układach próżniowych. Są to zespoły szklanych lub metalowych zbiorników, zaworów próżniowych, połączeń rurowych, sondy próżniomierzy i pomp próżniowych. Próżnię wytwarza się poprzez mechaniczne usunięcie cząsteczek powietrza poza obszar naczynia (pompy przepływowe: rotacyjna i dyfuzyjna) lub poprzez absorpcję (pompy sorpcyjne).
Pompę próżniową charakteryzują dwie wartości: ciśnienie końcowe i szybkość pompowania. Ciśnienie końcowe jest miarą próżni ustalonej po bardzo długim czasie pompowania, zależne jest w dużym stopniu od prądu wstecznego w pompie (ilości gazu „cofającego się” ). Ciśnienie końcowe dla pompy rotacyjnej równe jest w przybliżeniu 10-1 - 10-2 Pa, a dla pompy dyfuzyjnej 10-6 - 10-7 Pa. Szybkość pompowania S oznacza objętość gazu usuniętego w jednostce czasu. Definiowana jest funkcja zależności ciśnienia wewnątrz opróżnianego pojemnika od czasu (S = const) oznaczane p(t). Korzystając z definicji szybkości pompowania (dV = S dt) i różniczkując prawo Boyle'a - Mariotte'a otrzymujemy dla pojemnika o pojemności V:
pV = const
![]()
![]()
![]()
Całkując stronami:
![]()
czyli:
![]()
Próżniomierze mają za zadanie podać miarę próżni. Rozróżniamy próżniomierze: mechaniczne, hydrostatyczne, kompensacyjne, cieplnoprzewodnościowe, jonizacyjne i inne. Manometr mechaniczny dokonuje pomiaru różnicy ciśnień pomiędzy ciśnieniem zewnętrznym, a ciśnieniem wewnątrz pojemnika wykorzystując odkształcenie elementu mechanicznego, które przenoszone jest na wskazówkę. Próżniomierz termoprzewodnościowy wykorzystuje zależność zmiany przewodnictwa cieplnego rozrzedzanego gazu od ciśnienia, jonizacyjny zaś bazuje na zmianie oporu elektrycznego rozrzedzanego gazu.
Barograf jest to przyrząd służący do ciągłego zapisu wartości ciśnienia atmosferycznego. Zbudowany jest on z puszki ,wewnątrz której zachowane jest stałe ciśnienie i wskazówki z pisakiem, której wychylenie proporcjonalne jest do różnicy ciśnień: atmosferycznego i wzorcowego.
Próżniomierz McLeoda jest próżniomierzem kompensacyjnym, w którym ciśnienie mierzy się odczytując różnicę poziomów rtęci w dwóch kapilarach. Zbudowany jest on z kapilary kompensacyjnej i porównawczej, zbiornika gazu, przewodu głównego i mieszkowego zbiornika rtęci. Pomiaru dokonuje się metodą liniową (w kapilarze porównawczej poziom rtęci jest ustalony na pewnej wysokości, odpowiadającej poziomowi h0 w drugiej kapilarze) i metodą kwadratową (kapilara porównawcza jest całkowicie wypełniona rtęcią).
Technika próżniowa znajduje szerokie zastosowanie: w procesach produkcji związków o wysokiej czystości chemicznej i przyrządów półprzewodnikowych, w lampach kineskopowych, termosach i naczyniach do przechowywania skroplonych gazów. Największą jakość próżni uzyskuje się w komorach akceleratorowych - rzędu 10-9 Pa.
3. Wyniki pomiarów
warunki zewnętrzne:
p0 = 992 hPa ± 1 hPa - ciśnienie atmosferyczne
T0 = 23 °C ± 1 °C = 296 K ± 1 K - temperatura otoczenia
V0 = 0,24 dm3 - objętość przewodów łączących
V1 = 1,24 dm3 - objętość zbiorników nr 0, 1, 2, 3, 4
V2 = 2,48 dm3 - objętość zbiorników nr 5, 6, 7
błędy pomiaru:
pomiar ciśnienia manometrem mechanicznym:
![]()
Klasa dokładności 1,5, korzystając ze wzoru:
Bezwzględna wartość błędu wartości ciśnienia mierzonego za pomocą manometru równa jest więc (152+12)1/2 ≈15 hPa, po uwzględnieniu błędu pomiaru ciśnienia atmosferycznego (który wynosi ± 1hPa).
pomiar ciśnienia próżniomierzem oporowym:
Nie znana jest klasa dokładności, więc jedyną informacją o możliwym błędzie jest podziałka logarytmiczna. Błąd pomiaru uzależniony jest więc od wysokości mierzonego ciśnienia. Wartości maksymalnego błędu zostaną umieszczone w tabelce.
pomiar czasu:
Δt = 1 s
zależność ciśnienia od czasu odpompowywania układu pompą rotacyjną:
|
Ciśnienie w układzie p [hPa] |
Czas pompowania t [s] |
manomet r |
992 ± 1 |
0 |
|
792 ± 15 |
1,52 |
|
592 ± 15 |
3,72 |
|
392 ± 15 |
7,37 |
|
292 ± 15 |
10 |
|
192 ± 15 |
13,49 |
|
92 ± 15 |
19,99 |
|
72 ± 15 |
22,24 |
|
52 ± 15 |
24,64 |
|
32 ± 15 |
28,89 |
|
12 ± 15 |
36,98 |
próżniom. |
1 +500 -0,1 |
146 |
|
0,5 ±0,1 |
190 |
|
0,4 ±0,1 |
230 |
|
0,3 ±0,1 |
277 |
|
0,2 ±0,1 |
396 |
|
0,15 +0,1 -0,05 |
486 |
|
0,1 +0,05 -0,01 |
881 |
|
0,09 ±0,01 |
1050 |
|
0,085 ±0,05 |
1500 |
zależność ciśnienia od objętości:
Ciśnienie p [hPa] |
Objętość V [dm3] |
Odwrotność obj. 1/V [1/dm3] |
|
|
|
992 |
1,24 |
0,806 |
697 |
1,48 |
0,676 |
392 |
2,72 |
0,368 |
272 |
3,96 |
0,252 |
212 |
5,2 |
0,192 |
172 |
6,44 |
0,155 |
126 |
8,92 |
0,112 |
97 |
11,4 |
0,088 |
82 |
13,88 |
0,072 |
wyznaczenie masy powietrza użytego w drugiej części ćwiczenia:
Korzystając ze wzoru:
pV = nRT
można wyznaczyć n - ilość moli powietrza
p = 992 hPa ± 1hPa = 99200 Pa ± 100 Pa
V = V0 = 1,24 dm3 = 0,00124 m3
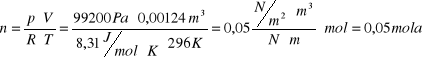
T = 296 K ± 1 K
R = 8,31 J / (mol*K)
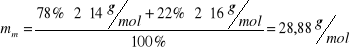
masę molową mm powietrza (78% N2, 22% O2) można obliczyć ze średniej ważonej:
Szukana masa powietrza wynosi więc:
![]()
By znaleźć błąd, jakim obarczona jest ta wartość, należy skorzystać z prawa przenoszenia błędów:
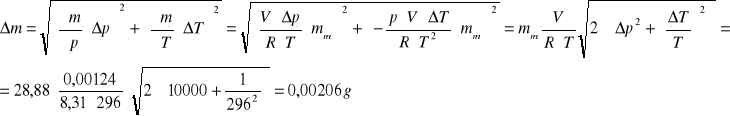
Ostatecznie więc szacowana masa powietrza biorącego udział w doświadczeniu wynosi 1,444 g ± 0,00206g
4. Wnioski
wykres zależności ciśnienia od czasu pompowania
Przedstawione na załączonym wykresie punkty zgodnie z rozważaniami teoretycznymi z punku 1. powinny stanowić linię prostą. Biorąc pod uwagę fakt spadku wydajności pompy spowodowany nie najlepszą szczelnością układu można stwierdzić, iż założenia teoretyczne były prawidłowe - można dopasować prostą do pierwszych jedenastu punktów wykresu. Pozostałe punkty znacznie od tej prostej odbiegające wskazują na fakt, że dla ciśnień zbliżonych do granic możliwości pompy spadek ciśnienia następuje znacznie wolniej, na co ma wpływ szczelność układu.
wykres zależności ciśnienia od odwrotności objętości układu
Druga część doświadczenia miała sprawdzić słuszność prawa Boyle'a - Mariotte'a poprzez porównanie wyników doświadczenia z prostą teoretyczną przechodzącą przez punkt p0 = 0 i 1/V0 = 0 oraz p = 992hPa ± 1hPa (ciśnienie atmosferyczne) i 1/V1 gdzie V1 = 1,24 dm3 (objętość pierwszego zbiornika). Na załączonym wykresie większość punktów pokrywa się w zakresie błędu z prostą teoretyczną. Pierwsze trzy punkty pomiarowe odbiegają jednak od oczekiwanych rezultatów. Przyczyną tego jest fakt, iż w doświadczeniu zostało użyte powietrze, które nie spełnia założeń modelu gazu doskonałego. Błędy pomiaru wynikły także z bardzo niskiej rozdzielczości podziałki manometru. Inną przyczyną niezgodności wyników z założeniami teoretycznymi jest również zmiana temperatury gazu przy rozprężaniu, co wpływało na jego ciśnienie.
- 5 -
![]()
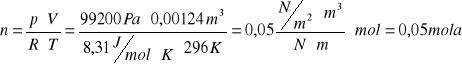
![]()
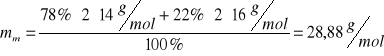
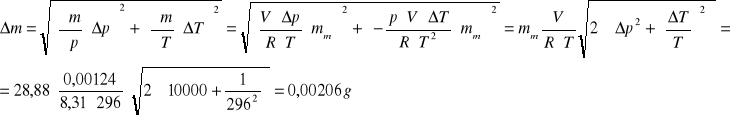
Wyszukiwarka
Podobne podstrony:
LAB1, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 001 WA~1
25OPR, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 025 IN~1
LAB01, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 001 WA~1
LAB22TAB, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 022 ST~1
LAB25 , Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 025 IN~1
LAB25!, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 025 IN~1
LAB13 , Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 013 LE~1
LABTAB, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 002 WA~1
LAB25 ~1, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 025 IN~1
25WSTEP, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 025 IN~1
LAB02C, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 002 WA~1
LABOR2D, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 002 WA~1
FIZYKA~6, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 013 LE~1
LAB51, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 051
LABFIZ, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 013 LE~1
LAB1, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 001 WA~1
więcej podobnych podstron