Wydział EAiE	Imię Nazwisko: 1.Bartosz Ławniczek 2.Grzegorz Majka		Rok: I		Grupa: 3		Zespół: 3
Pracownia fizyczna I	Temat: Interferencja fal akustycznych						Nr ćwiczenia: 25
Data wykon: 20.03.1998	Data oddania:	Zwrot do pop:		Data oddania:		Data zalicz:	Ocena:

Cel ćwiczenia:

Wyznaczenie prędkości dźwięku w gazach w temperaturze pokojowej, metodą interferencji fal akustycznych, przy użyciu rury Quinckego.

Wprowadzenie:

Dowolne zaburzenie mechaniczne rozchodzi się w ośrodku ciągłym w postaci fali. W ciałach stałych mogą rozchodzić się fale poprzeczne i podłużne, w cieczach i gazach wyłącznie podłużne. Za fale dźwiękowe uważamy fale o częstotliwościach od 20 Hz do 20 kHz, gdyż są one słyszalne przez ucho ludzkie. Niesłyszalne przez nas infra- i ultradźwięki rozchodzą się w podobny sposób.

W ciele stałym prędkość dźwięku v określa stosunek modułu sprężystości E do gęstości ρ ośrodka.

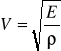
W przypadku gazów moduł Younga zastępujemy adiabatycznym modułem sprężystości, równym iloczynowi ciśnienia p i stosunku ciepeł właściwych χ= C_p/C_v. Pod ciśnieniem atmosferycznym w zwykłych temperaturach większość gazów wykazuje własności zbliżone do własności gazu doskonałego. Z tego względu p/ρ dla gazów w tych warunkach można zastąpić przez RT/μ. (R - uniwersalna stała gazowa, T - temperatura bezwzględna,  - ciężar cząsteczkowy)

Podstawiając tą wartość do poprzedniego wzoru otrzymujemy wzór na prędkość dźwięku w gazach:

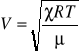
Jak widać ze wzoru, prędkość dźwięku nie zależy od ciśnienia a jest wprost proporcjonalna do pierwiastka kwadratowego z temperatury

Rozchodzenie się dźwięku opisuje równanie falowe. W przypadku, gdy źródłem fali dźwiękowej jest układ wykonujący drgania harmoniczne, powstaje fala sinusoidalna. Amplituda takiej fali, rozchodzącej się wzdłuż drogi x, jest dana wzorem :

y=y_msin(kx-ωt)

gdzie: ω = 2  

Gdy w pewnym punkcie przestrzeni spotykają się dwie lub więcej fal, zachodzi zjawisko interferencji.

Rozpatrzmy superpozycję dwóch fal, które wyszły z tego samego źródła i do pewnego punktu A ośrodka docierają dwiema różnymi drogami różnej długości x1 i x2. Amplitudy fal są równe odpowiednio

y₁ = y_max1sin(kx₁-ωt)

y₂ = y_max2sin(kx₂-ωt)

a amplituda wypadkowa

y_w = y₁ + y₂

Po przekształceniu trygonometrycznym wykorzystującym równanie cosinusów otrzymujemy

y_m =

gdzie ϕ jest funkcją x₁, x₂ i λ.

Pierwszy czynnik tego iloczynu daje amplitudę drgania wypadkowego w rozważanym punkcie. Czynnik ten osiąga wartość minimalną, gdy

cos k (x₁ - x₂) = -1

Ma to miejsce wtedy, gdy x₁ - x₂ =  (n - ¹/₂), to znaczy gdy różnica dróg, po których biegną fale, jest równa nieparzystej wielokrotności połówek długości fali. Pierwsze minimum otrzymujemy dla n = 1, drugie dla n = 2 itd.

Znając długości fali  można wyliczyć prędkość rozchodzenia się dźwięku w gazie ze wzoru:

v =   (   częstotliwość )

Tabela wyników pomiarowych:

Częstotliwość źródła [Hz]

Położenie kolejnych minimów [mm]

Różnica położeń kolejnych minimów [mm]

Długość fali λśr [m]

Prędkość dźwięku v [m/s]

(v - vśr)^2 [m^2/s^2]

a1

a2

a3

a4

a5

Δ1a

Δ2a

Δ3a

Δ4a

---