Wydział : EAiE	Imię i nazwisko : 1. Daniel Olchowy 2. Dariusz Wieczorek		Rok : I		Grupa : 7		Zespół : I
Pracownia fizyczna I	Temat ćwiczenia : Zależność okresu drgań od amplitudy.					Ćwiczenie nr: 2
Data wykonania: 27-II-98	Data oddania:	Zwrot do poprawy:	Data oddania:	Data zaliczenia:				Ocena:

Cel ćwiczenia:

Celem ćwiczenia jest zapoznanie się z ruchem drgającym i parametrami pisującymi ten ruch. Wyznaczenie zależności okresu drgań od amplitudy dla układu zbliżonego do wahadła matematycznego.

Wprowadzenie:

Ruchem harmonicznym nazywamy ruch w którym wychylenie jest sinusoidalną funkcją czasu. Z ruchem takim mamy do czynienia tylko w tedy , gdy działająca siła zwrotna jest proporcjonalna do wychylenia. Dla ruchu harmonicznego okres drgań nie zależy od amplitudy , gdyż równanie różniczkowe opisujące je jest liniowe .

Ruch dowolnego wahadła , zarówno matematycznego jak i fizycznego , jest harmoniczny jedynie dla małych wychyleń , dla których słuszne jest przybliżenie

sinq≈q . Dla wychyleń dużych przybliżenie to nie jest słuszne , a równanie opisujące drganie wahadła :

nie jest liniowe . Rozwiązaniem jego jest ruch okresowy , ale już nie harmoniczny Okres tego ruchu zależy od amplitudy Q. Zależność tę można przedstawić w postaci szeregu:

wzór ten można przekształcić do postaci :

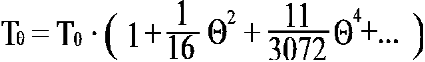
Powyższe równanie nie uwzględnia tłumienia wynikającego z oporów powietrza. Częstość kołowa drgań tłumionych jest nieco mniejsza niż częstość kołowa drgań tłumionych i wynosi :

gdzie - współczynnik tłumienia.

Wartość współczynnika tłumienia można oszacować z szybkości zaniku amplitudy jako :

gdzie q1 , q2 oznacza amplitudy zmierzone w odpowiednich chwilach t1 i t2.

Wyniki :

F1 [°]	f2 [°]	t [s]	F [rad] p	T [s]	T-T0 T0

2

---