Prognozowanie na podstawie jednorównaniowego modelu ekonometrycznego
prognoza punktowa,
prognoza przedziałowa.
Modele nieliniowe.
Funkcja produkcji.
1. Klasyfikacja prognoz
Prognozowanie ekonometryczne - wnioskowanie o przyszłych wartościach zmiennej endogenicznej na podstawie modelu wyjaśniającego kształtowanie się tej zmiennej.
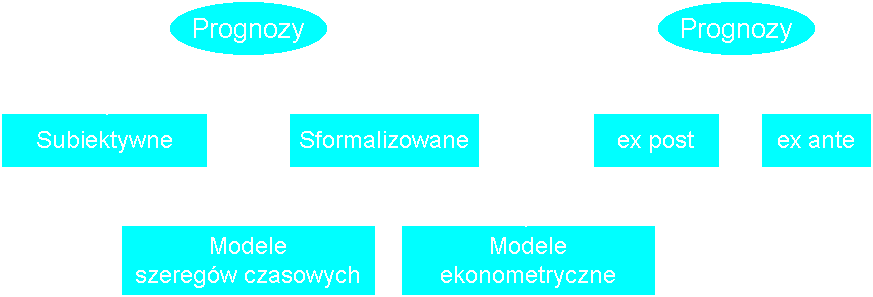
2. Prognoza punktowa
Oszacowany model ekonometryczny
![]()
Okres prognozy: t > n.
Wektor wartości zmiennych objaśniających dla okresu prognozy:
![]()
Prognoza punktowa:
![]()
Średni błąd predykcji ex ante:
![]()
Względny średni błąd predykcji ex ante:
![]()
3. Przykład
Oszacowany model:
![]()
Okres prognozy: t = 6.
Wartości zmiennych objaśniających:
x16 = 5,
x26 = 12.
Prognoza punktowa:
![]()
Średni błąd predykcji ex ante:
![]()
Względny średni błąd predykcji ex ante: v6 = 2,24%
4. Prognoza przedziałowa

Przedział ufności:
![]()
![]()
Prognoza punktowa w przypadku autokorelacji
(t = n + s):
![]()
5. Przykład
Poziom istotności: a = 0,05.
Liczba stopni swobody: u = 2.
Wartość krytyczna: t0,005;2 = 4,303.
Prognoza przedziałowa: (37,04 ; 44,96)
6. Dokładność prognoz ex post
średni absolutny błąd predykcji:
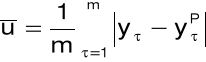
współczynnik Theila:
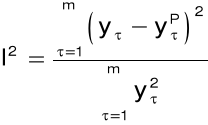
7. Modele liniowe
mają prostą interpretację,
często stanowią dobrą aproksymację relacji nieliniowych,
są łatwe w estymacji oraz weryfikacji statystycznej,
są postacią modeli nieliniowych po ich linearyzacji.
8. Nieliniowości modeli
Modele nieliniowe względem zmiennych:
np. Y = a0 + a1X + a2X2 + e,
proste, bo podstawiamy Z = X2 i Y = a0 + a1X + a2Z + e.
Modele nieliniowe względem parametrów
np. Y = a0 + a12X + a2Z + e,
trudne metody estymacji,
czasami pomaga linearyzacja modelu,
sprawdzian: jeśli każda pochodna cząstkowa zmiennej Y względem parametrów modelu jest niezależna od wszystkich parametrów modelu, to taki model jest liniowy względem parametrów.
9. Typowe modele nieliniowe
Model wielomianowy:
Y = a0 + a1X + a2X2 + ... + akXk + e.
Model logarytmiczny: Y = a0 + a1lnX + a2lnZ + e.
Model hiperboliczny: Y = a0 + a1/X + a2Z + e.
Model z interakcjami:
Y = a0 + a1X + a2Z + a3XZ + e.
![]()
Model potęgowy:
Model wykładniczy:
![]()
Model S-krzywej:
![]()
10. Funkcja produkcji
Funkcja produkcji - zależność między nakładami czynników produkcyjnych w pewnym procesie, a wielkością wytworzonego produktu.
Ekonometryczna funkcja produkcji - model jednorównaniowy, w którym zmienną objaśnianą jest produkcja Y, a zmiennymi objaśniającymi są nakłady J czynników produkcji Xj:
Y = f(X1,X2,...,XJ)
Nakłady:
kapitału:K,
pracy: L.
11. Założenia o funkcji produkcji
Funkcja produkcji: Y = f(K,L).
Założenia:
Y > 0, K > 0, L > 0,
izokwanty produkcji (linie stałego produktu), tj. linie którym odpowiada ta sama wartość produkcji, czyli Y0 = f(K,L), są wypukłe,
funkcja produkcji jest ciągła i dwukrotnie różniczkowalna.
12. Własności funkcji produkcji
Produkcyjność krańcowa czynnika produkcji jest dodatnia:
fK > 0, fL > 0.
Produkcyjność krańcowa czynnika jest malejąca:
fKK < 0, fLL < 0.
Krańcowa produkcyjność jednego czynnika wzrasta w miarę zwiększania nakładów drugiego czynnika:
fKL > 0, fLK > 0.
12. Własności funkcji produkcji
Funkcja f jest jednorodna:
f(lK,lL) = lrf(K,L),
r = 1 - stałe korzyści skali,
r > 1 - rosnące korzyści skali,
r < 1 - malejące korzyści skali.
Czynniki produkcji są wzajemnie zastępowalne:
KSS = dK/dL = - fL/fK - substytucja pracy przez kapitał.
13. Funkcja Cobba - Douglasa
Wieloczynnikowa funkcja produkcji Cobba - Douglasa:
![]()
Dwuczynnikowa funkcja produkcji Cobba - Douglasa:
Y = aKbLce, a > 0, b > 0, c >0,
produkcyjności krańcowe są dodatnie:
fK = abKb - 1L > 0, fL = acKbLc -1 > 0,
produkcyjności krańcowe są malejące:
fKK = ab(b - 1)Kb -2Lc < 0, fLL = ac(c -1)KbLc - 2 < 0,
produkcyjność jednego czynnika rośnie przy zwiększaniu nakładów drugiego: fKL = fLK = abcK b - 1 L c - 1 > 0,
14. Dwuczynnikowa funkcja produkcji Cobba - Douglasa
funkcja jest jednorodna stopnia b + c:
f(lK,lL) = l b + c f(K,L), 1 - alfa
krańcowa stopa substytucji:
KSS = - c/b * K/L,
efektywność produkcji względem nakładów czynników produkcji są stałe:
EKY = b, ELY = c.
Szukasz gotowej pracy ?
To pewna droga do poważnych kłopotów.
Plagiat jest przestępstwem !
Nie ryzykuj ! Nie warto !
Powierz swoje sprawy profesjonalistom.
![]()
![]()
![]()
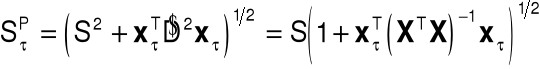
![]()
![]()
![]()
![]()

![]()
![]()
![]()
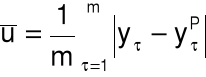
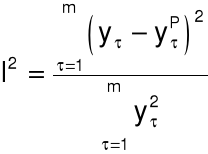
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
252
239 252
plik (252)
252 id 31184 Nieznany
252 SC DS300 R SKODA SUPERB B 02 XX
neurologia strony 225-252, neurologia, GIEŁDA, neurologia
252
odp 252 286 id 331986 Nieznany
252, Scenariusz lekcji
252 752204 renowator mebli artystycznych
Pervin Psychologia osobowości str 252 275, 281 309
252
252
252
ref soc 252, Dokumenty(2)
252 coldplay trouble
252
252
więcej podobnych podstron