• 5.18. Aby sporządzić plan terenu w skali 1:10 000, zrobiono zdjęcie ze śmigłowca, który wzniósł się na wysokość h = 2000 m. jaka była ogniskowa obiektywu aparatu fotograficznego, za pomocą którego uzyskano zamierzo­ny efekt ?

• 5. 19. Przesuwając soczewkę między ekranem a przedmiotem, wzdłuż osi optycznej soczewki, w dwóch jej położeniach otrzymano ostry obraz przed­miotu na ekranie. W pierwszym położe­niu soczewki wysokość obrazu była równa H₁ = 3 cm, a w drugim - H₂ = 1 2 cm. Jaka jest wysokość przedmiotu h?

• 5.20. Soczewka o ogniskowej f=16 cm tworzy na ekranie obraz przed­miotu powiększony p₁ = 8 razy. Nie zmieniając odległości między przedmio­tem i ekranem, usunięto soczewkę i wsta­wiono inną w takie miejsce, że na ekra­nie powstał obraz przedmiotu powięk­szony p₂ = 2 razy. Jaka jest ogniskowa drugiej soczewki?

• 5.21. Przesuwając przedmiot i ekran, wykonano pomiary odległości y soczewki od ekranu, na którym uzyskiwano obrazy przedmiotu o różnych powiększeniach p. Na wykresie na rysunku 5.9 przedstawiono zależności p(y). Oblicz ogniskową soczewki.

Rys. 5.9

• 5.22. Dwa punktowe źródła świa­tła znajdują się w odległości a = 40 cm od siebie. Między nimi w odległości b=10 cm od jednego z nich znajduje się soczewka skupiająca. Jaka jest ognisko­wa tej soczewki, jeżeli obrazy obydwóch źródeł światła się pokrywają?

• 5.23. Promienie świetlne rozcho­dzące się z punktowego źródła padają­ce na soczewkę skupiającą dają wiązkę rozbieżną, w której skrajne promienie tworzą kąt α = 90° (rysunek 5.10.). Od­ległość źródła od soczewki x = 3 cm, a średnica soczewki d = 8 cm. Jaka jest ogniskowa soczewki?

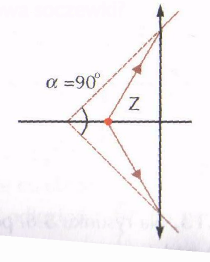
Rys. 5.10

• 5.24. Na rysunku 5.11. pokaza­no punktowe źródło światła wirujące ze stałą szybkością v wokół osi optycznej soczewki skupiającej. W jakiej odległo­ści od soczewki i z jaką szybkością po­rusza się obraz tego źródła? Środek okrę­gu, po którym porusza się źródło znaj­duje się w odległości x = 3 f, gdzie f jest ogniskową soczewki.

Rys.5.11

• 5.25. Wzdłuż osi optycznej soczewki o ogniskowej f = 10 cm umiesz­czono krótki patyczek, którego jeden ko­niec znajduje się w odległości x₁ = 12 cm, a drugi w x₂ = 14 cm od soczewki. Ile razy jest powiększony obraz patyczka?

• 5.26. Na drodze zbieżnej wiązki światła ustawiono soczewkę o ognisko­wej f= 10 cm, co spowodowało, że wiązka została skupiona w odległości y = 5 cm za soczewką. Gdzie skupiłaby się wiązka, gdyby nie było soczewki?

•5.27. Jak zmieni się ogniskowa soczewki płasko-wypukłej położonej płaską stroną na powierzchni wody? Współczynnik załamania materiału so­czewki jest większy od współczynnika załamania wody.

a) zmaleje

b) nie zmieni się

c) wzrośnie

d) soczewka stanie się soczewką rozpraszającą

•5.28. Ze szkła o współczynniku załamania n= 1,5 wykonano soczewkę płasko-wypukłą tak, że promień krzywi­zny części wypukłej R= 25 cm. Jaka jest ogniskowa soczewki umieszczonej w powietrzu?

• 5.29. Zamrażając wodę w odpo­wiedniej foremce, uzyskano płasko-wypukłą soczewkę z lodu, którego współ­czynnik załamania d, = 1,31. Promień krzywizny wypukłej części soczewki /?= 10 cm. Jak zmienią się właściwości fi­zyczne soczewki po włożeniu jej do wody o temperaturze f = 0° C w porów­naniu z właściwościami tej soczewki w powietrzu? Współczynnik załamania wody n₂ = 1,33.

a) soczewka stanie się soczewką rozpraszającą

b) odległość ogniskowa soczewki nieco zmaleje, ale soczewka bę­dzie nadal skupiała światło

c) jej właściwości się nie zmienią

d) odległość ogniskowa soczewki nieco wzrośnie, ale pozostanie¹ ona soczewką skupiającą

• 5.30. Punktowe źródło światła umieszczono w ognisku soczewki roz­praszającej. Do soczewki przystawiono drugą soczewkę skupiającą, co spowo­dowało, że wiązka światła po przejściu przez obydwie soczewki była równoległa. Jaki powinien być stosunek ogniskowej soczewki skupiającej do ogniskowej soczewki rozpraszającej?

1. f_s : f_r = 0,5

2. f_s : f_r = 1

3. f_s : f_r = 2

4. f_s : f_r = 5

• 5.31. Umieszczona w powietrzu soczewka dwuwypukła wykonana ze szkła o współczynniku załamania n_s = 1,5 charakteryzowana jest ogniskową f = 10 cm. Soczewkę zanurzono w wodzie o współczynniku załamania n_w = 1,33. Jaka jest ogniskowa soczewki, gdy znajduje się ona w wodzie?

• 5.32. Pewien gatunek szkła ma współczynnik załamania promieni fioletowych n₁ = 1,8, a czerwonych n₂=l,75. Z tego szkła wykonano soczewkę dwuwypukłą o promieniach krzywizny R₁=R₂=R=0,40 m. W jakiej odległości od siebie znajdują się ogniska tej soczewki dla promieni fioletowych i czerwonych?

• 5.33. Dwuwypukła soczewka o promieniach krzywizn R₁ = 12,5 cm i R₂ = 25 cm tworzy w odległości y = 25 cm obraz pewnego przedmiotu oddalonego od soczewki o x= 100 cm. Jaki jest współczynnik załamania cieczy, do której włożono soczewkę, jeżeli ognisko­wa soczewki w tej cieczy f= 1 m?

• 5.34. Oblicz ogniskową soczew­ki dwuwypukłej znajdującej się w po­wietrzu o promieniach krzywizn R₁ = 20 cm, R₂ = 80 cm, wykonanej z krysz­tału NaCl o współczynniku załamania światła n= 1,54.

• 5.35. Z tego samego szkła wykona­no dwie soczewki. Jaka jest zdolność sku­piająca soczewki 2., jeśli wiadomo, że zdol­ność skupiająca soczewki 1. D₁ = 4 D?

Rysunek 5.12.

a) D₂ = -8 D

b) D₂ = -4 D

c) D₂ = 4D

d) D₂ = 8 O

• 5.36. Dwie soczewki skupiające o ogniskowych odpowiednio równych f₁ i f₂, stykając się stanowią układ optycz­ny. Jaką zdolność skupiającą D ma so­czewka, która może zastąpić układ tych dwóch soczewek?

1. D=f₁+f₂ / f₁•f₂

2. D= f₁- f₂ / f₁•f₂

3. D= f₁+f₂ / 2•f₁•f₂

4. D= f₁- f₂ / 2•f₁•f₂

• 5.37. Jak ustawić na wspólnej osi optycznej dwie soczewki skupiające o różnych ogniskowych, aby równoległa wiązka światła padająca na pierwszą soczewkę po przejściu przez układ pozostała wiązką równoległą?

a) takie ustawienie nie jest możliwe

b) należy soczewki ze sobą zetknąć

c) należy soczewki ustawić w odle­głości od siebie f₁+f₂ /2 od siebie

d) należy soczewki ustawić w odle­głości f₁+f₂ od siebie

• 5.38. Na popularnych lupach znajdujących się w sprzedaży często umieszczany jest napis „5x", „8x" itp. Określa on, ile razy lupa powiększa oglą­dane obiekty. Jaki napis powinien być umieszczony na lupie, której zdolność skupiająca D= 8 D?

a) „3x"

b) „5x"

c) „8x"

d)„10x"

• 5.39. Aby zobaczyć pozorny po­większony obraz przedmiotu, należy przedmiot umieścić w odległości x = 5 cm przed soczewką. Oblicz zdolność sku­piającą soczewki i powiększenie obrazu.

• 5.40. Pewien człowiek chciał określić zdolność skupiającą swoich okularów. W tym celu trzymając je po­ziomo pod lampą, tak długo zmieniał ich wysokość, aż uzyskał ostry obraz lampy na podłodze. Odległość lampy od pod­łogi l = 2,5 m, a okularów od podłogi y = 0,5 m. Jaka była zdolność skupiają­ca soczewek tych okularów?

1. D = 1,5 D

2. D = 2,0 D

3. D = 2,5 D

4. D = 3,0 D

• 5.41. Niewielka świeczka stoi w odległości x= 10 cm od soczewki, któ­rej zdolność skupiająca D = 5 D. Jaka jest odległość obrazu świeczki od so­czewki? Jaki to obraz?

• l 5.42. Jaka jest ogniskowa soczew­ki, której zdolność skupiająca jest rów­na D= -4 D?

a) f = -25 cm

b) f = -4 cm

c) f = ą cm

d) f = 25 cm

• 5.43. Soczewka rzutnika o zdol­ności skupiającej D= 8 D ustawiona jest tak, że jej ognisko F, znajduje się w środ­ku płaskiego zwierciadła ustawionego pod kątem a = 45° do płaszczyzny so­czewki (rysunek 5.13.). Poniżej ogniska F₂ soczewki, w odległości l= 2,5 mm od niego, znajduje się oświetlone od spodu przeźrocze, którego obraz przez soczewkę i zwierciadło rzutowany jest na ekran E. Jakie wymiary ma obraz na ekranie, jeże­li wymiary przeźrocza wynoszą a x b = 4 cm x 6 cm?

Rysunek 5.13

• 5.44. Przedmiot znajduje siew odległości n = 4 razy większej od soczewki niż jej ogniskowa. Jakie jest powiększenie obrazu?

• 5.45. Zataczając latarką krąg o promieniu r= 0,5 m, którego środek leży na osi optycznej soczewki o zdolności skupiającej D = 2 D, otrzymano na ekranie za soczewką ostry obraz w postaci wirującego punktu świetlnego o promieniu R = 1,5 m. W jakiej odległości od soczewki znajduje się ekran?

• 15.46. Szklana soczewka umieszczona w powietrzu ma zdolność skupia­jącą D = 5 D. Jaka będzie jej zdolność skupiająca po zanurzeniu w wodzie? Współczynnik załamania szkła soczewki n_} = 1,5, wody n₂ = 1,3, powietrza n_} = 1.

• l 5.47. Płasko-wypukła soczewka wykonana jest ze szkła o współczynni­ku załamania n, a promień krzywizny so­czewki jest równy R. Jak zmieni się zdol­ność skupiająca D soczewki, jeżeli jej płaską stronę posrebrzymy tak, że stanie się płaskim zwierciadłem dla promieni padających od jej strony wypukłej?

1. dwukrotnie zmaleje

2. nie zmieni się

3. dwukrotnie wzrośnie

4. będzie równa zeru

• l 5.48. Pewien człowiek może czy­tać bez wysiłku druk umieszczony w od­ległości x= 1 m od oka. Jaką zdolność skupiającą powinny mieć okulary, dzię­ki którym będzie on mógł czytać swo­bodnie druk umieszczony w odległości dobrego widzenia L = 0,25 m?

• 5.49. Krótkowidz posługując się okularami o zdolności skupiającej D = -5 D, może czytać tekst umieszczony w odległości dobrego widzenia L = 25 cm. W jakiej odległości od oka powinien umieścić tekst, aby mógł go czytać bez okularów?

• 5.50. Dalekowidz używając oku­larów o zdolności skupiającej D = 1 D, czyta swobodnie tekst umieszczony w od­ległości x= 0,5 m. Jaka powinna być zdol­ność skupiająca nowych okularów, aby za ich pomocą mógł czytać tekst z odle­głości dobrego widzenia L = 0,25 m?

6. DrganIa

Wprowadzenie

• RUCH HARMONICZNY

Ruchem harmonicznym prostym nazywamy ruch drgający odbywający się pod wpływem siły o wartości wprost proporcjonalnej do wychylenia ciała z położenia równowagi:

Rysunek I

F = -kx (25)

gdzie: F jest wartością siły powodującej wychylenie, k- współczynnikiem sprężystości, x- wychyleniem z położenia równowagi.

Zwrot siły F jest przeciwny do zwrotu wychylenia x. Współczynnik k charakteryzuje dane ciało

Okres drgań punktu materialnego om masie m, drgającego pod wpływem siły wyraża się wzorem:

T = 2π√m/k (26)

• WYCHYLENIE, SZYBKOŚĆ l PRZYSPIESZENIE W RUCHU HARMONICZNYM

Wychylenie z położenia równowagi jest opisane następującą funkcją czasu:

x(t) = Asin (ωt+ϕ₀), (27)

gdzie: A jest amplitudą drgań, ω- częstością kołową (pulsacją), ϕ₀ - fazą początkową.

Szybkość w ruchu harmonicznym:

v(t) = Aωcos(ωt+ϕ₀). (28)

Przyspieszenie w ruchu harmonicznym:

a(t) = -Aω²sin(ωt+ϕ₀). (29)

Ze wzorów (27) i (29) wynika:

a = -ω²x. (30)

Częstotliwość kołowa ω związana jest z częstotliwością f i okresem drgań T zależnością;

ω = 2πf = 2π/T. (31)

• WAHADŁO MATEMATYCZNE
Okres drgań wahadła matematycznego przy niewielkich wychyleniach nie zależy od|
amplitudy (przy wychyleniach do 20° błąd przybliżenia okresu nie przekracza 0,007)
i jest równy:

T = 2π√l/g (32)

gdzie: l jest długością wahadła, g- przyspieszeniem ziemskim (zwykle 9,81 m/s²).

• ENERGIA DRGAŃ HARMONICZNYCH

Energia kinetyczna wyrażana jest wzorem: E_k = mv²/2

po podstawieniu v ze wzoru (28) mamy:

E_k = ½ mω²A²cos(ω+ϕ₀). (33)

Energia potencjalna drgań jest równa:

E_p = ½ kx².

Po podstawieniu x ze wzoru (27) oraz zastąpieniu, na podstawie wzorów (26) i (31), k przez mω², mamy:

E_p = ½ mω²A²sin²(ωt+ϕ₀). (34)

Energia całkowita E_h = E_k + E_p nie zależy od czasu i wyraża się wzorem:

E_h = ½ mω²A². (35)

Przykładowe zadania

• 1.Ciało o masie m= 0,04 kg drga ruchem harmonicznym. Amplituda tego ruchu A = 3 cm, a całkowita energia drgań E_h = 5 mJ. Oblicz okres drgań i maksymalną szybkość ciała.

• DANE

masa ciała m - 0,04 kg

amplituda ruchu harmonicznego A = 3 cm

całkowita energia drgań E_h = 5 mJ

• SZUKANE

okres drgań T maksymalna szybkość v_m

• ROZWIĄZANIE

Do obliczenia okresu T wykorzystamy wzór (35) E_h = ½ mωA² oraz wzór(31) ω = 2π/T. Stanowią one układ dwóch równań z dwiema niewiadomymi ω i T. Podstawiając częstotliwość kołową ω ze wzoru (31) do wzoru (35), otrzymamy:

E_h = 2mπ²A² / T².

Po pomnożeniu obu stron równania przez T² i podzieleniu przez E_h mamy:

T² = 2mπ²A² / E_h.

Wyciągamy pierwiastek kwadratowy z obu stron równości:

T = πA√2m/ E_h.

Po podstawieniu danych liczbowych T= 0,377 s.

Energia całkowita drgań jest liczbowo równa energii kinetycznej w chwili, gdy ciało osiąga szybkość maksymalną:

E_h.=mv²_m/2.

Po pomnożeniu obu stron równania przez 2, podzieleniu przez m i wyciągnięciu ui< wiastka kwadratowego uzyskamy:

v_m=√2E_h/m.

Po podstawieniu danych liczbowych otrzymamy v_m = 0,5 m/s.

• ODPOWIEDŹ

Okres drgań T= 0,377 s, a szybkość maksymalna v_m = 0,5 m/s.

•2. Na rysunku II pokazano zależność wartości siły sprężystości F działającej na ciało o masie m = 0,04 kg od wychylenia x. Oblicz maksymalną szybkość ciała v_m w ruchu drgającym o amplitudzie A = 3 cm. Przyjmij fazę początkową ϕ₀ = 0.

Rysunek II

•DANE

wykies zależności F(x)

masa ciała m= 0,04 kg

amplituda drgań A = 3 cm

•SZUKANE

szybkość maksymalna v_m

•ROZWIĄZANIE

Współczynnik sprężystości k wyznaczymy z wykresu, obliczając wartość bezwzględ­ną współczynnika kierunkowego (nachylenia) prostej. Prosta przechodzi przez punkty (0,0) i (50, -800). Stosunek różnicy rzędnych do różnicy odciętych tych punktów:

k = ΔF/Δx = 800N/50m = 16 N/m.

Ze wzorów (26): T = 2π√m/k i (31): ω = 2πf = 2π/T, a po przekształceniu mamy:

ω = √k/m

Skorzystamy również ze wzoru na szybkość w ruchu harmonicznym (28):

v(t) = Aωcos(ωt) (przy założeniu, że faza początkowa jest równa zeru). Szybkość

jest największa wówczas, gdy cos(ωt) = 1 i wynosi:

v_m = Aω = A√k/m.

Po podstawieniu danych liczbowych otrzymamy v_m = 0,6 m/s.

•ODPOWIEDŹ

Maksymalna szybkość ciała w omawianym ruchu harmonicznym wynosi v_m = 0,6 m/s.

• 3. Dwa wahadła matematyczne o długościach ^ = 162 cm i /₂ = 72 cm w pewnej chwili znajdują się w tej samej fazie drgań. Ile drgań muszą wykonać wahadła, aby ponownie znaleźć się w jednakowej fazie ruchu?

• DANE

długości wahadeł l₁ = 162 cm, l₂ = 72 cm

jednakowe fazy w chwili t₀

• SZUKANE

liczba drgań n₁

liczba drgań n₂

• ROZWIĄZANIE
Ponieważ ta sama faza drgań następuje okresowo, co przedział czasu T, 2T, 3T itd.
obydwa wahadła będą miały takie same fazy, jak na początku, gdy: pierwsze wahadło
wykona n₁ drgań w czasie T= n₁ T₁ , a drugie w tym samym czasie t= n₂T₂ wykona n₂

pełnych wahnięć. Stąd równość:

n₁ T₁= n₂T₂.

Podstawiając okresy drgań ze wzoru (28), mamy:

n₁2π√l₁/g = n₂2π√l₂/g.

Jest to równanie z dwiema niewiadomymi: n₁ i n₂ Można je jednak rozwiązać, gdyż poszukiwane liczby muszą być liczbami całkowitymi. Po podzieleniu obu stron rów­nania przez 2π i podniesieniu do kwadratu mamy:

n₁² l₁/g = n₂² l₂/g.

Po pomnożeniu obu stron przez g.

n₁²l₁ = n₂²l₂

Obie strony równania dzielimy przez l₁ n₂² i otrzymujemy:

(n₁/ n₂)² = l₂/l₁.

Po podstawieniu wartości liczbowych l₁ i l₂ uzyskujemy:

(n₁/ n₂)² = 72 cm/162 cm = 72/162 = 36/81.

Poszukujemy liczb całkowitych, których stosunek kwadratów jest równy 36/81. Zauważmy, że 81 = 9² i 36 = 6². Możemy napisać równość:

(n₁/ n₂)² = (6/9)².

Stąd:

n₁/ n₂ = 6/9.

Wartości n₁ = 6, n₂ = 9 są rozwiązaniem, ale szukamy najmniejszych liczb spełniających ten rachunek. Ponieważ 9 i 6 mają wspólny dzielnik 3, szukanymi liczbami są n₁ = 2 i n₂ = 3.

•ODPOWIEDŹ

Te same fazy powtórzą się, gdy wahadła wykonają n₁ = 2 oraz n₂ = 3 drgania.

ZADANIA

• 6.1. W wesołym miasteczku na n₁ = 4 obroty karuzeli przypada n₂ = 12 pełnych wahnięć huśtawki. Z jaką czę­stotliwością waha się huśtawka, jeżeli ka­ruzela w czasie t= 30 s wykonała 6 peł­nych obrotów?

a) 2 Hz b) π Hz

c)1/π Hz d)4π Hz

• 6.2. Jak zmieni się okres drgań kuli zawieszonej na sprężynie, jeżeli spręży­nę tę skrócimy o połowę?

a) zmaleje

b) nie zmieni się

c) wzrośnie

d) nie wiadomo, po skróceniu sprę­żyny ruch nie będzie harmoniczny

• 6.3. Ciężarek o masie m = 1 kg zawieszony swobodnie na sprężynie roz­ciąga ją o Δx = 9,81 mm. Jaki będzie okres drgań T ciężarka, jeżeli zostanie wprawiony w ruch drgający?

• 6.4. Ciężarek o masie m, leżący na gładkim stole, przymocowany jest do sprężyny, której drugi koniec jest unie­ruchomiony. Sprężynę rozciągnięto siłą o wartości F= mg przyłożoną do ciężar­ka, a następnie puszczono. Napisz rów­nanie opisujące wychylenie ciężarka z położenia równowagi w funkcji cza­su, wiedząc, że współczynnik sprężysto­ści sprężyny jest równy k.

F

Rysunek 6.1.

• 6.5. Sprężysta kulka odbija się cy­klicznie od stalowej płyty pionowo do góry bez strat energii. Po każdym odbi­ciu kulka wznosi się na wysokość h = 0,98 m. Jaki jest okres drgań tej kulki?

• 6.6. Jaka jest masa ciężarka m po­wieszonego na sprężynie o współczyn­niku sprężystości k = 20 Nm^-1, jeżeli okres ruchu harmonicznego T= 3,14 s?

• 6.7. Metalowa kula wisi na sprę­żynie o długości l i współczynniku sprę­żystości k. Wprawiona w ruch harmo­niczny w kierunku pionowym drga z czę­stotliwością f₁ Jaka będzie częstotliwość drgań, jeżeli sprężynę przetniemy na dwie równe części, a kulę zawiesimy na obu równolegle zawieszonych częściach sprężyny?

Rysunek 6.2

• 6.8. Metalowa kula zawieszona jest na sprężynie i drga ruchem harmo­nicznym o okresie T. Jaki będzie okres drgań kuli drewnianej o takim samym promieniu, przymocowanej do tej sprę­żyny zamiast kuli metalowej? Gęstość kuli drewnianej jest n= 9 razy mniejsza od gęstości kuli metalowej.

• 6.9. Na sprężynie zawieszony jest ciężarek o masie m= 0,20 kg, który wpra­wiono w ruch drgający w płaszczyźnie pionowej, o amplitudzie A = 10 cm. Jaki jest okres drgań T tego ciężarka, jeżeli pod działaniem siły F= 0,25 N sprężyna rozciąga się o Δl= 2 cm?

• 6.10. Stalowa kulka, zawieszona na długiej nici, wykonuje drgania harmoniczne. W pobliżu punktu równowagi od dołu zbliżono magnes. Jak zmieni się okres drgań kulki?

---