Wyznaczanie niezbędnej liczebności próby
Model 1
Minimalna liczebność próby niezbędna do oszacowania wartości średniej n na poziomie ufności 1-ά z maksymalnym błędem szacunku nie przekraczającym d obliczanym ze wzoru:
![]()
σ - odchylenie standardowe populacji
uά - wartość zmiennej losowej w standaryzowanym rozkładzie normalnym odczytana z tablicy rozkładu normalnego, dla przyjętego z góry współczynnika ufności 1-ά
d - dopuszczalny ustalony z góry maksymalny błąd szacunku średniej
Model 2
Minimalna liczebność próby przy estymacji średniej z nieznanym odchyleniem standardowym:
![]()
no - próba wstępna
n≤ no - liczebność próby wstępnej jest wystarczająca, gdy n≥ no, to trzeba dostosować do właściwej próby n-no elementów
Model 3
W przypadku, gdy możliwe jest przeprowadzenie badania wstępnego, to minimalna liczebność próby , która gwarantuje żądaną precyzję przy szacowaniu wskaźnika struktury p przy założonym maksymalnym błędzie szacunku d ze wzoru:
![]()
p - spodziewany rząd wielkości szacowanych wskaźników struktury
d - maksymalny dopuszczalny błąd szacunku
Model 4
Gdy nie znamy rządu wielkości szacowanego wskaźnika struktury, to wzór na minimalną liczebność przyjmuje postać:
![]()
Zadanie 1
Ile rodzin należących do określonej grupy zamożności należy wylosować niezależnie do próby by oszacować średnią miesięczną kwotę wydatków na cele kulturalne tych rodzin z dopuszczalnym maksymalnym błędem szacunku wynoszącym 10 zł. Wiadomo, że odchylenie standardowe populacji wynosi 80 zł., a przyjmowany współczynnik ufności 0,90 (wartość statystyczna 1,64)
![]()
Aby oszacować miesięczne wydatki na cele kulturalne z dopuszczalnym błędem 10 zł. do próby należy wylosować 173 rodziny.
Zadanie 2
W celu uzyskania przeciętnego dziennego czasu poświęcanego przez emerytów na oglądanie TV wylosowano do próby 10 osób i otrzymano dla nich średnią 3,75 godziny oraz odchylenie standardowe 1,10 godziny. Wyznaczyć niezbędną liczebność próby, dla ustalenia średniego czasu poświęcanego na oglądanie TV z dokładnością do 0,5 godziny, przy współczynniku ufności 0,95 (wartość statystyczna 2,262).
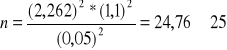
Aby oszacować średni dzienny czas poświecony przez emerytów na oglądanie TV należy wylosować 25 osób, czyli oprócz 10 już wylosowanych należy jeszcze wylosować 15 emerytów.
Zadanie 3
Jak liczna powinna być próba, by z maksymalnym dopuszczalnym błędem 3% przy współczynniku ufności 0,95 oszacować odsetek osób, które wezmą udział w najbliższych wyborach. Wyniki ostatniego sondażu przeprowadzonego przez OBOP wskazują, że udział w wyborach deklaruje 38% uczestników badania (wartość statystyczna 1,96).
![]()
Chcąc zagwarantować postulowaną dokładność należy do próby wylosować 1006 osób.
Zadanie 4
Wśród rodzin pewnego osiedla zamierza przeprowadzić się ankietę w celu oszacowania odsetka rodzin chcących mieć stałe połączenie z Internetem. Ile rodzin należy wylosować do próby, aby z maksymalnym błędem próby 5% przy współczynniku ufności 0,90 oszacować odsetek rodzin zainteresowanych stałym połączeniem z Internetem (wartość statystyczna 1,64).
![]()
Do próby należy wylosować 269 rodzin.
Przedział ufności dla wariancji
Estymacji przedziałowej wariancji dokonujemy i dla dużej i dla małej próby.
Model 1
Zakładamy ze populacja generalna ma rozkład normalny o nieznanej średniej i odchyleniu standardowym. Z populacji tej wylosowano dużą próbę n>30, to przedział ufności dla 1-ά wyznaczamy według wzoru:
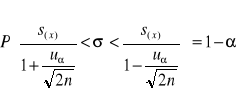
Względną precyzję szacowanego parametru wyznaczamy według wzoru:
![]()
Model 2
Populacja generalna ma rozkład normalny, nie znamy ani średniej ani odchylenia standardowego. Pobieramy próbę n<30 wówczas przedział ufności dla wariancji wyznaczamy według wzoru:
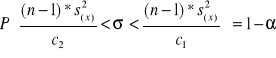
c1, c2 - wartości zmiennych wyznaczane z tablic CHI² dla n-1 stopnia swobody oraz współczynnik ufności 1-ά
Dla określonego współczynnika ufności 1-ά wartość c1 znajdujemy z tablic rozkładu dla prawdopodobieństwa 1-½ά, natomiast c2 dla ½ά.
Zadanie 1
W pewnym mieście w losowo wybranych 200 gospodarstwach domowych badano miesięczne wydatki na usługi telekomunikacyjne. Okazało się, że odchylenie standardowe miesięcznych opłat wyniosło 28 zł. Zakładając, ze badana cecha ma rozkład normalny oszacować metodą przedziałową nieznane odchylenie standardowe miesięcznych wydatków na usługi telekomunikacyjne w tym mieście, przyjmując współczynnik ufności 0,90 i ocenić precyzję dokonanego szacunku (wartość statystyczna 1,64)
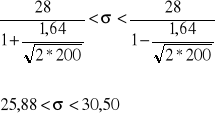
![]()
Przedział liczbowy o końcach 25,88 i 30,50 złotych z prawdopodobieństwem 0,90 obejmuje nieznane odchylenie standardowe wydatków na usługi telekomunikacyjne. Błąd względny wynosi 8,2% co wskazuje na dostateczną precyzję oszacowania i dopuszcza do wnioskowania na podstawie próby.
Zadanie 2
W celu zbadania zróżnicowania wielu kandydatów na studia niestacjonarne II stopnia w UEP wylosowano 10 osób i otrzymano średni wiek 24,3 lata i odchylenie standardowe wynoszące 4,7 lat. Zakładając, że badana cecha ma rozkład normalny oszacować metodą przedziałową nieznane odchylenie standardowe wieku kandydatów na studia niestacjonarne II stopnia, przyjmując współczynnik ufności 0,90 (wartość statystyczna c1 = 3,325 i c2 = 16,919)
UWAGA!!! - c2 zawsze jest większą wartością !!!
![]()
![]()
![]()
Przedział liczbowy o końcach 11,75 i 59,79 z prawdopodobieństwem 0,90 pokrywa nieznaną wariancję wieku wszystkich kandydatów na studia niestacjonarne II stopnia w UEP. Natomiast przedział liczbowy o końcach 3,43 i 7,73 z prawdopodobieństwem 0,90 pokrywa nieznane odchylenie standardowe wieku kandydatów.
Przedział ufności dla współczynnika korelacji (Pearsona)
Model
Dwuwymiarowy rozkład dwóch cech mieszanych X, Y, jest normalny lub zbliżony do normalnego. Losujemy dużą próbę i dla tej próby wyznaczamy współczynnik korelacji p
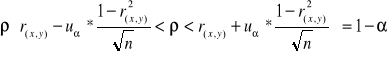
Zadanie 1
Na podstawie 500 obserwacji ustalono współzależności między poziomem dochodów a oszczędności. Uzyskano współczynnik korelacji N(x,y) = 0,82. Przyjmując współczynnik ufności 1-ά = 0,95 zbudować przedział ufności dla współczynnika korelacji w populacji generalnej (wartość statystyczna 1,96).
UWAGA!!! Współczynnik Pearsona nie może przekroczyć 1. !!!
![]()
![]()
Przedział liczbowy o końcach 0,791 i 0,849 z prawdopodobieństwem 0,95 pokrywa nieznaną wartość współczynnika korelacji Pearsona.
Weryfikacja hipotez statystycznych
Weryfikacja to sprawdzenie hipotez rozkładów lub założeń populacji generalnej.
Hipoteza statystyczna to sąd dotyczący rozkładu lub wartości pewnych parametrów określonej zmiennej wydany bez przeprowadzenia badania wyczerpującego.
Hipoteza parametryczna to przypuszczenia dotyczące parametrów populacji.
Hipoteza nieparametryczna to przypuszczenia dotyczące rozkładu populacji.
Hipoteza zerowa (H0) jest bezpośrednio sprawdzana
Hipoteza alternatywna (H1) jest konkurencyjna względem hipotezy zerowej (jest jej zaprzeczeniem).
Hipoteza zerowa zakłada, że pomiędzy estymatorem i parametrem nie ma statystycznie istotnej różnicy (zawsze ma znak równości).
Hipoteza alternatywna dopuszcza różnice między estymatorem i parametrem.
Testem statystycznym nazywamy regułę postępowania, która każdej możliwej próbie losowej przyporządkowuje decyzje przyjęcia bądź odrzucenia postawionej hipotezy. Wyróżnia się:
Testy parametryczne służą do weryfikacji hipotez parametrycznych.
Testy nieparametryczne służą do weryfikacji hipotez nieparametrycznych.
Błąd pierwszego rodzaju polega na odrzuceniu hipotezy zerowej gdy jest ona prawdziwa.
Błąd drugiego rodzaju polega na przyjęciu hipotezy zerowej gdy jest ona fałszywa.
Poziom istotności to prawdopodobieństwo popełnienia błędu pierwszego rodzaju. Jest on ustalany z góry jako dowolnie małe, bliskie zeru prawdopodobieństwo. Do najczęstszych należą 0,1; 0,05; 0,01; 0,001. Im wyższy poziom, tym większe prawdopodobieństwo odrzucenia hipotezy.
Testy istotności, to testy w których na podstawie wyników próby możemy podjąć decyzję o odrzuceniu hipotezy zerowej lub stwierdzamy, że nie ma podstaw do jej odrzucenia.
W testach nie podejmuje się decyzji o przyjęciu hipotez.
Obszar krytyczny to obszar odrzucenia hipotezy zerowej przy założeniu jej prawdziwości.
W zależności od hipotezy alternatywnej, wyróżnia się obszar krytyczny:
- dwustronny
- lewostronny
- prawostronny
Etapy testowania hipotez:
sformułowanie hipotezy zerowej i hipotezy alternatywnej
ustalanie poziomu istotności
wybór odpowiedniej statystyki testowej związanej z hipotezą zerową
określenie obszaru krytycznego
obliczenie wartości wybranej statystyki na podstawie wyników z próby
porównanie dwóch wartości: obliczonej z próby i odczytanej z tablic
podjęcie decyzji weryfikującej
Test istotności dla wartości średniej populacji generalnej
Model 1
Populacja generalna ma rozkład normalny ze znanym odchyleniem standardowym. Z populacji tej wybieramy n - elementową próbę. Na podstawie wyników tej próby weryfikujemy hipotezę zerową, że średnia populacji generalnej jest równa wartości hipotetycznej, według hipotezy alternatywnej jest różna.
H0::m = mo H1::m ≠ mo
![]()
Jeżeli: |u|≥uά - są podstawy do odrzucenia hipotezy zerowej
|u|≤uά - nie ma podstaw do odrzucenia hipotezy zerowej
W tych testach nie podejmuje się decyzji przyjęcia.
Model 2
Populacja generalna ma rozkład normalny o nieznanej średniej o odchyleniu standardowym. Z populacji tej pobieramy małą próbę, w oparciu o wyniki tej próby weryfikujemy hipotezę zerową:
![]()
mo - wartość hipotetyczna
|t|≥tά - odrzucamy hipotezę zerową na korzyść hipotezy alternatywnej
|t|≤tά - nie ma podstaw do odrzucenia hipotezy zerowej
Model 3
Zakładamy, że populacja generalna ma rozkład normalny lub inny, ale nie znamy ani średniej, ani odchylenia standardowego. Z populacji pobieramy dużą próbę (n>30).
Do weryfikacji hipotezy zerowej wykorzystuje się u:
![]()
Konstrukcja przebiega identycznie jak w modelu 1.
Zadanie 1
Wiadomo, że rozkład stażu pracy pracowników pewnego zakładu jest normalny z odchyleniem standardowym wynoszącym 2,3 lata. Na podstawie próby liczącej 16 pracowników stwierdzono, że średni staż pracy wynosi 7,4 lata. Czy na poziomie istotności 0,05 można twierdzić, że średni staż pracy pracowników w tym zakładzie jest większy od 7 lat (wartość krytyczna 1,64).
H0::m = 7 H1::m > 7
![]()
u<uά → Nie ma podstaw do odrzucenia hipotezy zerowej.
Zadanie 2
Czy prawdą jest, że średni czas realizacji zamówienia na dostarczenie pizzy do domu konsumenta wynosi 28 minut i jeżeli w 17 elementowej próbie takich zamówień średni czas realizacji to 24 minuty i odchylenie standardowe to 10 minut. Przyjąć poziom istotności 0,05 (wartość krytyczna 2,12).
H0::m = 28 H1::m ≠ 28
![]()
|t|<tά → Nie ma podstaw do odrzucenia hipotezy zerowej.
Zadanie 3
Wysunięto przypuszczenie, że przeciętny czas dokonania zakupów przez klientów w pewnym supermarkecie w Poznaniu wynosi 65 minut. W celu sprawdzenia tego przypuszczenia wylosowano niezależnie próbę liczącą 100 klientów i otrzymano dla niej średni czas 62 minuty i odchylenie standardowe 22,96 minut. Zakładając, że rozkład czasu zakupu jest normalny oraz, że poziom istotności jest równy 0,05 zweryfikować to przypuszczenie (wartość krytyczna 1,96).
H0::m = 65 H1::m ≠ 65
![]()
u<uά → Nie ma podstaw do odrzucenia hipotezy zerowej.
Test istotności dla dwóch wartości średnich
Model 1
Zakładamy, że dwie badane populacje generalne mają rozkłady normalne, ze znanymi wariancjami. Z populacji tych pobieramy dwie próby o liczebności n1 i n2
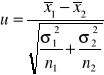
H0::m1 = m2 H1::m1 ≠ m2
H1::m1 > m2
H1::m1 < m2
Model 2
Badamy dwie populacje generalne mające rozkłady normalne o nieznanych odchyleniach standardowych. Z populacji pobieramy dwie małe próby o liczebności n1 i n2 < 30. Na podstawie prób wyznaczamy średnią i odchylenie standardowe.
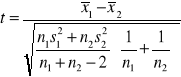
Porównujemy wynik ze statystyką rozkładu studenta o n1 + n2 stopnia swobody.
Model 3
Badamy dwie populacje generalne, gdy obu rozkłady są nieznane. Pobieramy dwie duże próby i weryfikujemy hipotezę:
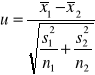
Model 4
Poziom wartości pewnej cechy dokonuje się przed lub po poddaniu badanych jednostek określonemu zabiegowi. W tej sytuacji przedmiotem analizy są różnice obserwowanych wartości.
Sprawdzamy H0 jest tu H0::mR = 0 mR → średnia w populacji różnic
![]()
gdzie:
![]()
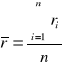
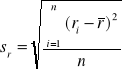
lub
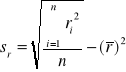
Przy założeniu, że hipoteza zerowa jest prawdziwa, statystyka t ma rozkład T-studenta z n-1 stopnia swobody.
Zadanie 1
Zbadano w losowo wybranych indywidualnych gospodarstwach rolnych województwa pomorskiego i wielkopolskiego. Średnie zużycie nawozu w kilogramach na hektar użytków rolnych. Wiadomo, że w obu województwach zużycie nawozów ma rozkład normalny z jednakowym odchyleniem standardowym 43kg/ha. Średnia z próby o liczebności n1 = 18 wylosowanej z województwa pomorskiego wyniosła 111,2 kg/ha natomiast liczebności n2 = 22 wylosowanej z województwa wielkopolskiego wyniosła 90,7 kg/ha. Przyjmując poziom istotności 0,05 sprawdzić hipotezę, że średnie zużycie nawozu w obu województwach jest jednakowa (wartość krytyczna 1,96).
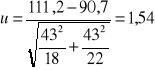
u<uά → Nie ma podstaw do odrzucenia hipotezy zerowej.
Zadanie 2
Czy prawdą jest, że średnie oceny z przedmiotów ścisłych uzyskanych przez studentów wydziału ekonomii i zarządzania nie różnią się istotnie, przy istotności 0,05. Jeśli na podstawie prób otrzymamy:
Wydział Ekonomii |
Wydział Zarządzania |
n1 = 15 |
n2 = 10 |
s1 = 0,35 |
s2 = 0,54 |
x1 = 3,93 |
x2 = 3,68 |
Rozkład na obu wydziałach średnich ocen jest normalny (wartość krytyczna 2,069)
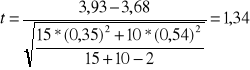
|t|<tά → Nie ma podstaw do odrzucenia hipotezy zerowej.
Zadanie 3
Powszechnie panuje pogląd, że średnia liczba dni opuszczonych w pracy przez kobiety z powodu choroby jest wyższa od absencji chorobowej mężczyzn. Na podstawie badania absencji w pracy uzyskano dla losowo wybranych prób n1 = 80 i n2 = 60. Następujące dane dotyczące czasu przebywania na zwolnieniu lekarskim:
`x1 = 31 s1 = 14,3
`x2 = 24 s2 = 9,6
Przyjmując poziom istotności 0,05 sprawdzić hipotezę, że absencja kobiet w pracy z powodu choroby jest wyższa aniżeli mężczyzn (wartość krytyczna 1,64).
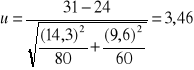
u>uά → Hipotezę zerową odrzucamy.
Zadanie 4
Pewnej grupie 10 pacjentów, którzy poddali się kuracji odchudzającej podano odpowiedni lek. Wyniki wagi w tej grupie przed kuracją i po kuracji umieszczono w tabeli poniżej:
Kg przed (x1) |
Kg po (x2) |
r=x1 - x2 |
r² |
102 |
97 |
5 |
25 |
113 |
102 |
11 |
121 |
97 |
88 |
9 |
81 |
122 |
118 |
4 |
16 |
109 |
99 |
10 |
100 |
98 |
87 |
11 |
121 |
87 |
81 |
6 |
36 |
101 |
98 |
8 |
64 |
119 |
108 |
11 |
121 |
105 |
97 |
8 |
64 |
SUMA |
83 |
749 |
|
Czy dane te dowodzą, że średnia waga przed i po kuracji jest jednakowa. Poziom istotności 0,1 (wartość krytyczna 1,8830
![]()
![]()
![]()
![]()
![]()
![]()
Hipotezę zerową odrzucamy.
Wyszukiwarka
Podobne podstrony:
Wnioskowanie statystyczne (wykład), UEP semestr I, Wnioskowanie statystyczne
statystyka III, UEP semestr I, Wnioskowanie statystyczne
Wyznaczanie temperatury Curie ferrytu [wnioski], Akademia Morska Szczecin, SEMESTR II, Fizyka, I sem
Prawo wykład, UEP semestr II, Prawo gospodarcze
II stopni 2 semestr plan zajęć
Psychologia Rozwojowa, II ROK, SEMESTR II, rozwój po adolescencji, sylabusy
zif sciaga, Studia UE Katowice FiR, II stopień, Semestr I, Zarządzanie instytucjami finansowymi
Szymura, II ROK, SEMESTR II, psychologia różnic indywidualnych, opracowania
Nęcka r. 6, II ROK, SEMESTR II, psychologia różnic indywidualnych, opracowania
Problemy i kwestie spoeczne wy II rok 2 semestr oraz III rok ciocia
Czarne Kwiaty, POLONISTYKA, II ROK SEMESTR ZIMOWY, HLP II ROK, romantyzm
metodologia - zagadneinia na egzamin, UKSW - Pedagogika, II rok - I semestr, Metodologia Badań Pedag
Rynek pracy, Wojskowa Akademia Techniczna - Zarządzanie i Marketing, Licencjat, II Rok, Semestr 3, R
Litera M, Pedagogika UŚ, Licencjat 2010-2013, II rok - semestr letni, Metodyka edukacji polonistyczn
więcej podobnych podstron