WOJSKOWA AKADEMIA TECHNICZNA
--------------------------------------------------------------------------------------------------------
LABORATORIUM FIZYCZNE
Grupa szkoleniowa C04J mgr inż. Andrzej Wiśniewski
stopień i nazwisko prowadzącego
GOLONKA Marcin
ŁUKASZEWICZ Jarosław
( imię i nazwisko słuchacza)
ocena końcowa ocena przygot.
do ćwiczenia
SPRAWOZDANIE
Z
PRACY LABORATORYJNEJ Nr 20
![]()
Temat: Wyznaczanie z pomiarów efektu magnetronowego.
1. Wstęp teoretyczny.
Jeżeli w jednorodnym polu magnetycznym wstrzelimy prostopadle do linii sił tego pola elektron
(o ładunku = -e) z prędkością ,to na ten ładunek działa siła:
![]()
gdzie:
![]()
-wektory pola elektrycznego i indukcji magnetycznej;
q -dodatni ładunek próbny;
![]()
-wektor prędkości ładunku;
W tym przypadku ![]()
=0,a q = -e, co prowadzi do związku :
![]()
Wynikiem działania siły na elektron będzie zakrzywienie jego toru w płaszczyźnie prostopadłej do kierunku wektora ![]()
.Ponieważ elektron wciąż porusza się w kierunkach prostopadłych do ![]()
,to kąt stale wynosi /2 i wartość bezwzględna siły Lorentza jest stała ,a więc torem elektronu jest okrąg .Zjawisko to zwie się
efektem magnetronowym .Posłuży ono do wyznaczenia wartości e/m.
Aby tego dokonać należy określić równocześnie trzy wielkości fizyczne :wielkość indukcji magnetycznej, prędkość wstrzelenia elektronu w pole oraz promień okręgu ,po którym on krąży w polu magnetycznym. Trudno jest wyznaczyć przy ustalonym polu magnetycznym krzywiznę toru elektronu ,więc w ćwiczeniu odbędzie się postępowanie odwrotne -- poszukamy pola o takiej indukcji B ,aby elektron krążył z góry wyznaczonym torze (określ. r).
Do tego służy dioda lampowa ,w której cienki drut (katoda) umieszczony jest w osi cylindrycznej anody .Elektrony wychodzące z tejże katody biegną promieniście do anody uzyskując przy tym prędkość
![]()
gdzie Ua jest napięciem przyłożonym między katodę i anodę .
W diodzie lampowej o promieniach anody i katody (odpowiednio ra i rk ;ra <rk)
tor elektronowy zostanie tak zakrzywiony ,aby był on styczny do powierzchni anody, czyli promień musi wynosić:
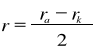
Wartość indukcji w której sytuacja ta nastąpi nazwiemy krytyczną i oznaczymy Bkr
Dioda lampowa umieszczona jest w polu magnetycznym wytwarzanym przez cewkę z prądem .Znając natężenie w polu magnetycznym prądu I płynącego w solenoidzie można wyznaczyć indukcję magnetyczną pola w pobliżu środka cewki za pomocą wzoru :
B = I
Gdzie oznacza empirycznie wyznaczoną stałą .
++
Rys. Układ w którym jest badany efekt magnetronowy
W doświadczeniu badana jest zależność prądu anodowego Ia funkcji B przy ustalonym napięciu anodowym.
2. Opis ćwiczenia.
2.1 Opis:
Poszukujemy takiego pola magnetycznego B przy którym elektrony będą krążyć po z góry określonym okręgu. W doświadczeniu badana jest zależność prądu anodowego Ia Przy ustalonym napięciu anodowym.
2.2 Dane:
δI = 5 mA błąd pomiaru prądu zasilającego cewkę
δIa = 5 μA błąd pomiaru prądu anodowego
δUa = 0,25 V błąd pomiaru napięcia anodowego
β = 1,35 ⋅ 10-2 T/A doświadczalnie wyznaczona stała dla cewki
δβ = 0,02 ⋅ 10-2 T/A błąd wyznaczenia stałej
ra = 0,8 mm promień anody
δra = 0,01 mm błąd promienia anody
rk = 0,05 mm promień katody
δrk = 0,01 mm błąd promienia katody
3. Wyniki pomiarów
I [mA] |
dla Ua=5 [V] |
dla Ua=8 [V] |
dla Ua=11 [V] |
|
|
Ia [μA] |
|
0 |
205 |
388 |
590 |
20 |
210 |
388 |
600 |
40 |
200 |
390 |
595 |
60 |
195 |
385 |
590 |
80 |
195 |
380 |
593 |
100 |
190 |
390 |
585 |
110 |
187 |
385 |
583 |
120 |
185 |
365 |
582 |
130 |
183 |
358 |
575 |
140 |
180 |
355 |
565 |
150 |
170 |
350 |
555 |
160 |
160 |
315 |
535 |
170 |
110 |
283 |
510 |
180 |
93 |
345 |
460 |
190 |
83 |
200 |
400 |
200 |
73 |
185 |
350 |
220 |
60 |
148 |
270 |
240 |
53 |
125 |
228 |
260 |
45 |
110 |
200 |
280 |
40 |
100 |
180 |
300 |
38 |
90 |
160 |
320 |
35 |
83 |
150 |
340 |
30 |
75 |
135 |
360 |
29 |
70 |
128 |
380 |
28 |
65 |
120 |
400 |
26 |
63 |
113 |
4. Wykresy (w załączeniu)
5. Zestawienie wyników
Ua [V] |
Ikr [A] |
Bkr [T] |
e/m [C/kg] |
(e/m)śr [C/kg] |
Błąd bezwzgl. (e/m)gr [C/kg] |
Błąd wzgl. (e/m) |
5 |
0,168 |
0,0022 |
1,38⋅1011 |
1,81⋅1011 |
7,07⋅109 |
0,05 |
8 |
0,182 |
0,0024 |
1,87⋅1011 |
|
6,18⋅109 |
0,03 |
11 |
0,198 |
0,0026 |
2,18⋅1011 |
|
5,44⋅109 |
0,02 |
6. Obliczenia
6.1 Obliczenie indukcji magnetycznej w pobliżu środka cewki Bkr
Korzystamy ze wzoru:
Bkr = β ⋅ Ikr
Bkr1 =1,35 ⋅ 10-2 T/A ⋅ 0,168 A = 2,27⋅ 10-3 T
Bkr2 =1,35 ⋅ 10-2 T/A ⋅ 0,182 A = 2,46⋅ 10-3 T
Bkr3 =1,35 ⋅ 10-2 T/A ⋅ 0,198 A = 2,67⋅ 10-3 T
6.2 Obliczanie e/m
![]()
Korzystamy z wzoru:
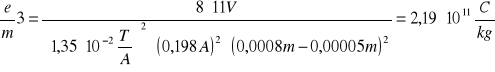
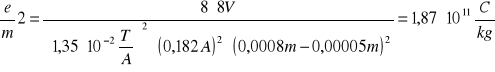
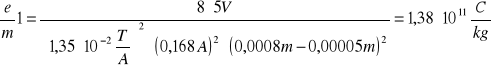
6.3 Obliczanie średniej arytmetycznej e/m
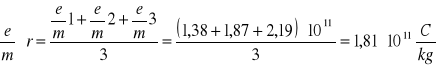
6.4 Obliczanie błędów:
6.4.1 Obliczanie błędów bezwzględnych granicznych dla poszczególnych pomiarów
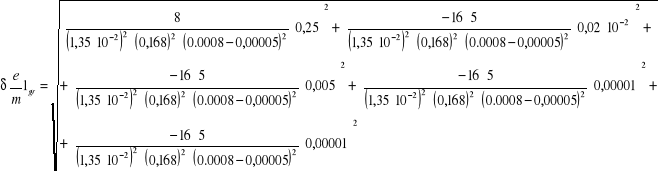
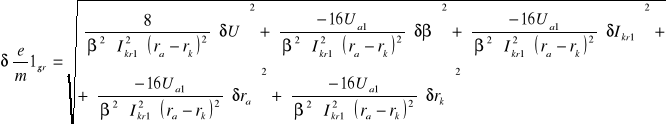
![]()
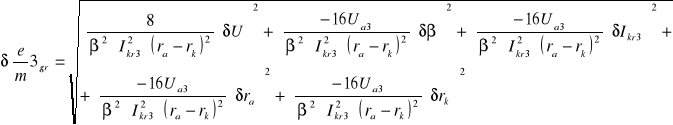
![]()
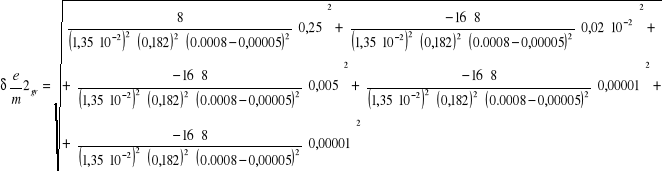
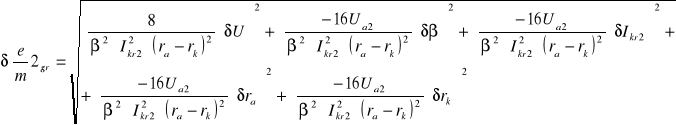
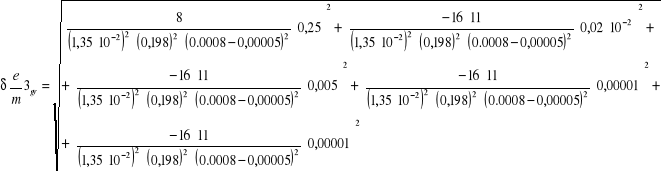
![]()
6.4.2 Obliczanie błędów względnych dla poszczególnych pomiarów
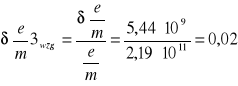
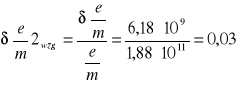
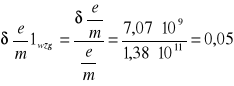
6.4.3 Obliczanie wartości średnich:
Średni błąd bezwzględny
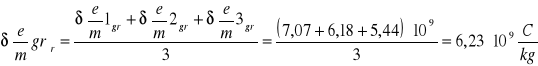
Średni błąd względny
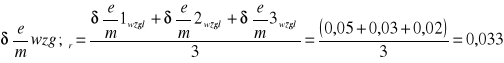
7. Wnioski
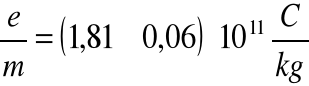
Wartość ładunku właściwego wyznaczona przez nas wynosi:
Niewiele odbiega ona od wartości teoretycznej, która wynosi 1,75⋅1011 C/kg.
Na błąd wpłynęła graficzna metoda wyznaczenia prądu krytycznego Ikr ,ale nasz wynik i obliczony błąd zawiera w sobie wartość teoretyczną ładunku właściwego, tak że cel został osiągnięty. Ponadto ćwiczenie zostało przeprowadzone z dużą dokładnością, o czym świadczy niewielki błąd względny, który wynosi 3,3 %.
![]()
![]()
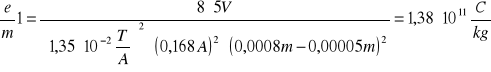
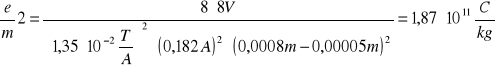
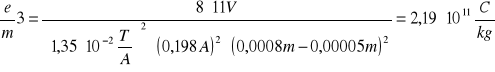
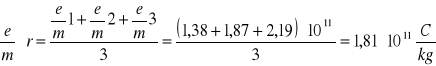
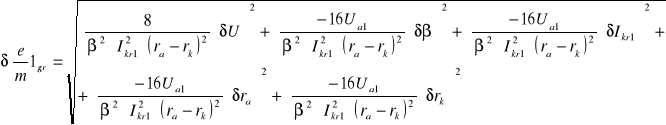
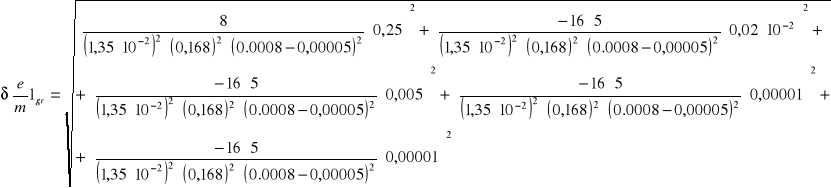
![]()
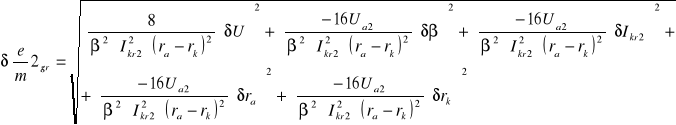
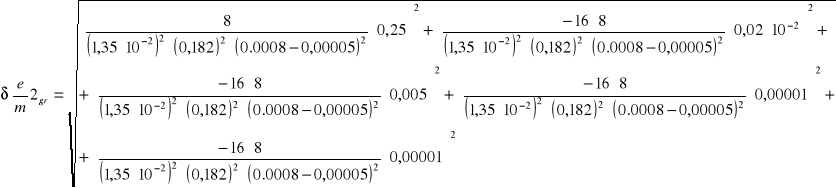
![]()
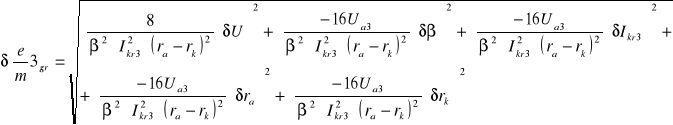
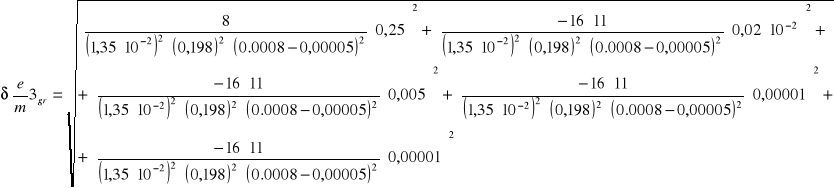
![]()
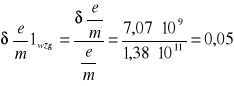
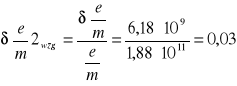
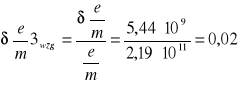
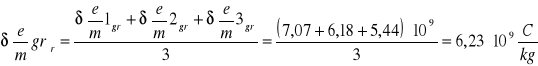
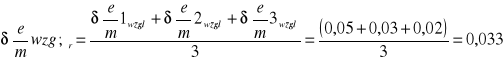
![]()
Wyszukiwarka
Podobne podstrony:
Zawal serca 20 11 2011
20 Rysunkowa dokumentacja techniczna
Prezentacja 20 10
20 2id 21226 ppt
20 H16 POST TRANSFUSION COMPLICATIONS KD 1st part PL
20 Tydzień zwykły, 20 środa
3 Analiza firmy 2015 (Kopia powodująca konflikty (użytkownik Maciek Komputer) 2016 05 20)
Prezentacja 20
plik (20)
20
20 Księga Przypowieści Salomona
01 Top 20 ports
cw 20 Instrukcja
chojnicki 1999 20 problemy GP
20 12id 21221
24 gold & 20's
Podstawy Teorii Okretow Pytania nr 4 (20) id 368475
więcej podobnych podstron