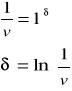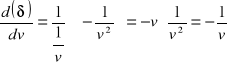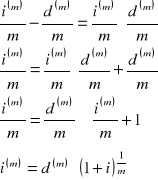KAROLINA KRÓLAK GR.2

ZADANIA II - ROZWIĄZANIA

ZADANIE 1. Dla równoważnych stóp
i
wyprowadzić formułę
.

ROZWIĄZANIE:

dla
mamy: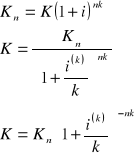
dla
mamy: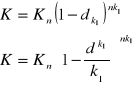

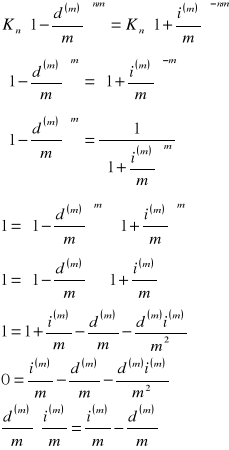
co było do pokazania.

ZADANIE 2. Korzystając z poprzedniego zadania pokazać, że
.

ROZWIĄZANIE:

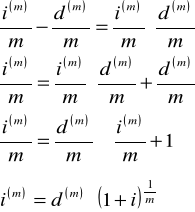
ZADANIE 3. Znając
oraz
wyznaczyć
.

ROZWIĄZANIE:

ZADANIE 4. Nominalna stopa oprocentowania ciągłego jest funkcją czasu
,
. Znaleźć średnią stopę oprocentowania ciągłego i równoważną efektywną roczną stopę oprocentowania składanego
w tym okresie.

Wskazówka:
,
.

ROZWIĄZANIE:

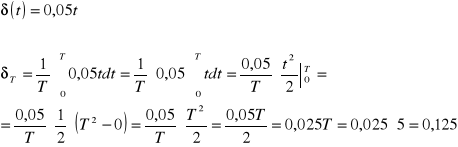
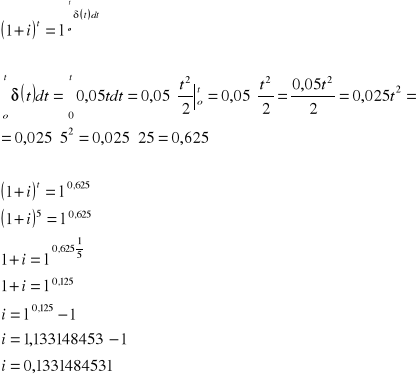
ZADANIE 5. Znaleźć zakumulowaną wartość $1 na koniec 15 lat, jeżeli
.

Wskazówka:
.

ROZWIĄZANIE:

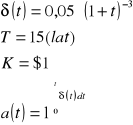
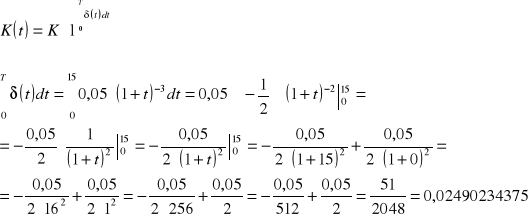
więc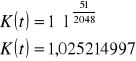

ZADANIE 6. Znaleźć efektywną roczną stopę oprocentowania składanego
obowiązującą w okresie trzech lat równoważną zmiennej stopie dyskonta w tym okresie:
w pierwszym roku
w drugim roku i
w trzecim roku.

Wskazówka:
.

ROZWIĄZANIE:

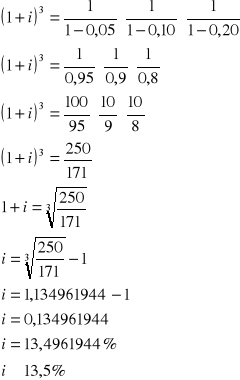
ZADANIE 7. Nominalna stopa oprocentowania ciągłego wyraża się wzorem

dla
. Dla dowolnego okresu rocznego pomiędzy rokiem
i
wyznaczyć równoważną nominalną stopę dyskontową
.

Wskazówka: Wyznaczyć najpierw
, następnie stopę dyskontową w okresie rocznym pomiędzy
i
(z zależności
)

i w końcu szukane
dla tego okresu.

ROZWIĄZANIE:

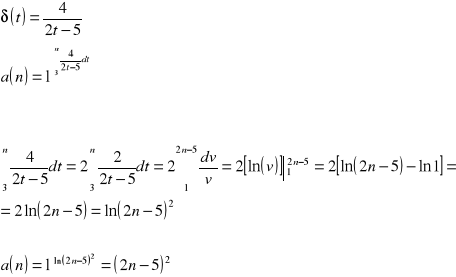
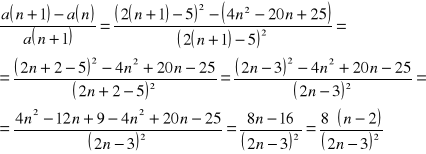
podstawiam n=4 i otrzymuję:

Korzystając ze wzoru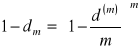
wyliczam szukane

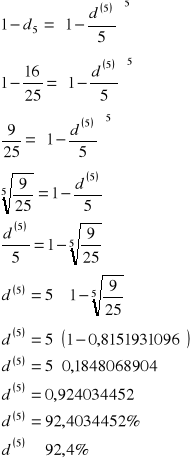
ZADANIE 8. Korzystając z poznanych zależności: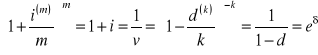

obliczyć następujące pochodne:

a)
, b)
, c)
, d)
, e)
.

ROZWIĄZANIE:

a)

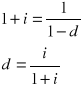
b)

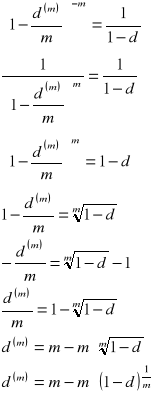
c)

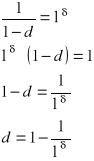
d)

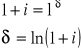
e)

---