Równanie Bernoulliego
Równanie Bernoulliego jest całką równania Eulera otrzymaną przy następujacych założeniach:
Płyn jest nielepki
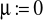
i nieprzewodzący ciepła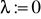
,Płyn jest barotropowy
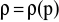
(gęstość jest jawną funkcją wyłącznie ciśnienia),Przepływ odbywa się w potencjalnym polu sił masowych, czyli
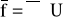
,
gdzie: U - potencjał pola jednostkowych sił masowych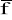
,Przepływ jest stacjonarny:
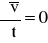
- pochodna lokalna prędkości równa zeru.
Wyprowadzenie:
W przypadku płynu nielepkiego równaniem ruchu (wynikającym z zasady pędu) jest równanie Eulera:
![]()
.
Ponieważ pole sił masowych jest potencjalne (zał. 3), więc ![]()
;
Ponieważ płyn barotropowy (zał.2), zatem istnieje funkcja ciśnienia ![]()
, która spełnia zależność: ![]()
(uzasadnienie zamieszczone poniżej − po wyprowadzeniu równania Bernoulliego). Zatem równanie Eulera przybiera postać:
![]()
![]()
, ![]()
(mnożymy skalarnie przez element linii prądu ![]()
, która w przypadku przepływu stacjonarnego pokrywa się z torem elementu płynu - operacja jest równoznaczna
z rzutowaniem na kierunek linii prądu wektorów będących składnikami obu stron równania. Od tego miejsca dalsze rozważania obowiązują tylko wzdłuż linii prądu):
![]()
;
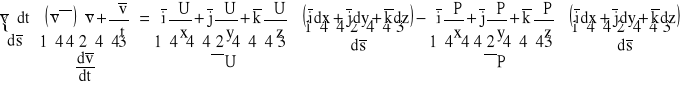
.
Ponieważ przepływ jest stacjonarny (ustalony) - zał.4, zatem pochodna lokalna prędkości ![]()
, zatem:
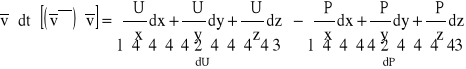
;
gdzie: dU; dP - różniczki zupełne funkcji U i P.
![]()
.
Przekształcimy lewą stronę równania, rozpisując pochodną konwekcyjną prędkości ![]()
:
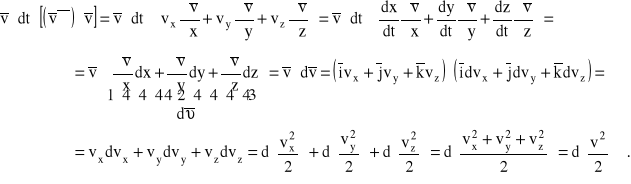
Powracając do przekształconego równania Eulera, otrzymujemy:
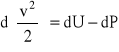
,
co można zapisać jako różniczkę zupełną wyrażenia:
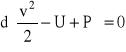
.
Po scałkowaniu otrzymujemy ogólną postać równania Bernoulliego:
![]()
.
Stała w tym równaniu obowiązuje tylko wzdłuż linii prądu (ponieważ dokonaliśmy rzuto-wania na kierunek linii prądu). Można wykazać, że w przypadku przepływu potencjalnego (pole prędkości bezwirowe) stała obowiązuje w całym obszarze przepływu (bez dowodu).
Uzasadnienie wykorzystanej wcześniej zależności:
Jeżeli ![]()
i ![]()
, to istnieje funkcja ciśnienia: ![]()
:
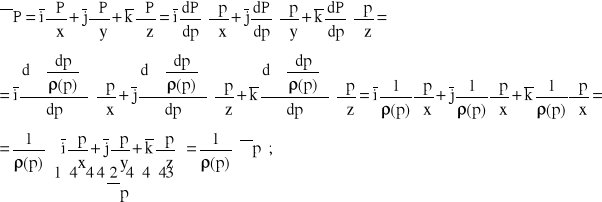
Uwaga: 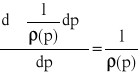
- pochodna całki jest równa funkcji podcałkowej.
Równanie Bernoulliego dla płynu doskonałego
w polu grawitacyjnym ziemskim
Płyn doskonały, zatem:
nielepki:
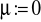
,nieściśliwy:
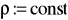
.
Funkcja ciśnienia przybiera w związku z tym postać:
![]()
.
Przepływ w polu grawitacyjnym ziemskim, czyli pole jednostkowych sił masowych: ![]()
, gdzie ![]()
- przyspieszenie ziemskie. Zatem:
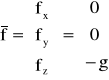
.
Na podstawie równania różniczkowego potencjału U pola jednostkowych sił masowych ![]()
, mamy:
![]()
,
skąd po scałkowaniu otrzymujemy:
![]()
.
Równanie Bernoulliego przybiera zatem postać:
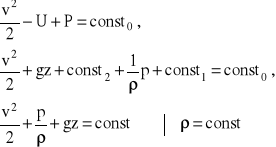
![]()
- równanie Bernoulliego w wymiarze ciśnienia,
lub po podzieleniu przez ![]()
:
![]()
- równanie Bernoulliego w wymiarze wysokości.
Interpretacja energetyczna
Pomnóżmy obie strony równania Bernoulliego (w wymiarze wysokości) przez ciężar ΔG elementu płynu o objętości ΔV i masie Δm:
![]()
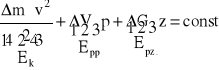
,
gdzie: Ek - energia kinetyczna elementu płynu,
Epp - praca sił ciśnieniowych (określana także jako energia potencjalna ciśnienia),
Epz - energia potencjalna położenia (względem przyjętego poziomu odniesienia).
Równanie Bernoulliego dla płynu doskonałego w polu grawitacyjnym ziemskim wyraża zatem zasadę zachowania energii w odniesieniu do elementu płynu o masie jednostkowej.
Interpretacja hydrauliczna
Suma:
„wysokości” położenia z, (rozumianej jako współrzędna położenia
względem przyjętego poziomu odniesienia)
„wysokości ciśnienia” ![]()
,
„wysokości prędkości” ![]()
jest stała wzdłuż linii prądu.
Dr inż. Janusz Bidziński Mechanika płynów - materiały pomocnicze dla studiów niestacjonarnych
1
![]()
![]()
![]()
![]()
Z2
Z1
V1
V2
Wyszukiwarka
Podobne podstrony:
Równanie ruchu różniczkowe i równanie Eulera, simr, mechanika płynów, mechanika płynów
Równanie Bernoulliego dla przepływu stacjonarnego płynu nieściśliwego, mechanika plynów
Równanie Bernoulliego, mechanika plynów
Równanie Bernoulliego ---przemiana adiabatyczna, mechanika plynów
Równanie Bernouliego-przemiana izotermiczna, mechanika plynów
Równanie Bernoulliego dla płynu ściśliwego, mechanika plynów
Rownanie Bernoulliego dla plynu idealnego, mechanika plynów
Równanie Bernouliego dla jednowymiarowego stacjonarnego przepływu strugi, mechanika plynów
Równanie równowagi płyny, mechanika plynów
Tematyka kolokwium z MP - materiał wykładów, simr, mechanika płynów, mechanika płynów
ćw.5 Kawitacja PRO, SiMR, mechanika płynów, Mechanika Płynów Sprawozdania
Mechanika płynów - podstawowe pojęcia 2, simr, mechanika płynów, mechanika płynów
mechanika płynów ściąga, SiMR, Mechanika płynów
ćw.1 Lepkość, SiMR, mechanika płynów, Mechanika Płynów Sprawozdania
I Mechanika płynów, SiMR, mechanika płynów, Praca domowa - skrypt MEGA, mechanika plynow, plyny
praca domowa 2(1), SiMR, mechanika płynów, Praca domowa - skrypt MEGA, mechanika plynow
Różniczkowe równanie ruchu Eulera, mechanika plynów
Równanie równowagi płyny, mechanika plynów
więcej podobnych podstron