Akademia Techniczno-Humanistyczna
w Bielsku-Białej
Wydział: Budowy Maszyn i Informatyki
Kierunek: Zarządzanie i Inżynieria Produkcji
Rok akademicki: 2011/2012; Semestr III

ĆWICZENIE NR 61

Wyznaczanie natężenia pola elektrycznego metodą sondy płomykowej.

Grupa: 106

1. Wstęp teoretyczny:

1. Natężenie i potencjał pola elektrycznego:

Oddziaływanie miedzy ładunkami elektrycznymi nie ma charakteru działania na odległość, lecz odbywa się za pośrednictwem pola elektrycznego. Pole elektryczne istnieje w przestrzeni otaczającej ciała naelektryzowane i przejawia się w postaci sił działających na ładunki elektryczne. W dowolnym układzie ładunków, każdy ładunek wytwarza własne pole elektryczne. W wyniku nałożenia się tych pól, powstaje pewne pole wypadkowe, które powoduje, że na każdy ładunek w rozważanym układzie działa określona siła. Pole elektryczne wytworzone przez nieruchome ładunki nazywa się polem elektrostatycznym.

W celu ilościowego opisania pola elektrycznego wprowadza się wielkość wektorową zwaną natężeniem pola elektrycznego
, określoną jako:

(1)

Gdzie:
- jest tzw. Ładunkiem próbnym, czyli bardzo małym dodatnim ładunkiem punktowym (w przypadku pola elektrostatycznego nieruchomym) umieszczonym w danym punkcie pola elektrycznego, a
- jest siłą działającą w polu na ten ładunek.

Ładunek
musi mieć małą wartość tak, by jego własne pole elektryczne nie zakłócało w wyraźny sposób pola, którego natężenie określamy.

Wektor
, jak wynika ze wzoru (1), ma kierunek zgodny z kierunkiem wektora siły działającej w polu elektrycznym na ładunek dodatni. W ogólnym przypadku natężenie pola elektrycznego może mieć różną wartość i kierunek w różnych punktach pola - wówczas
jest funkcja położenia:
. Szczególnym zaś przypadkiem pola elektrycznego jest pole jednorodne, w którym wektor natężenia pola ma wszędzie jednakową wartość i ten sam kierunek, czyli spełnia warunek
. W polu elektrostatycznym natężenie pola nie zmienia się w czasie, co można zapisać w postaci warunku:

Pole elektrostatyczne w danym punkcie przestrzeni można scharakteryzować podając jego potencjał elektryczny. Jest to wielkość skalarna określona jako stosunek energii potencjalnej
dodatniego ładunku próbnego
w danym punkcie pola do wielkości tego ładunku:

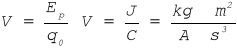
(2)

Ponieważ energia potencjalna
ładunku
w jakimś punkcie określona jest jedynie z dokładnością do stałej addytywnej, przyjmuje się, że energia potencjalna
ładunku nieskończenie odległego od układu wytwarzającego pole elektryczne jest równe zeru. Zatem potencjał elektryczny danego punktu pola jest równy liczbowo pracy na jednostkę ładunku wykonywanej przez siły pola przy przenoszeniu jednostkowego ładunku dodatniego z danego punktu do punktu nieskończenie odległego (lub do innego punktu, którego potencjał przyjmuje się umownie jako potencjał zerowy).

Różnice potencjałów
między dwoma punktami pola elektrycznego określamy jako napięcie elektryczne
:

(3)

2. Związek między wartością natężenia pola E i potencjałem V:

(4)

Powyższa zależność określa wartość natężenia pola elektrostatycznego jako stosunek spadku potencjału
na niewielkim odcinku prostopadłym do powierzchni ekwipotencjalnej

(powierzchnia równego potencjału) do długości
tego odcinka.

Znak „ - ” wynika stąd, że zwrot wektora
jest przeciwny do spadku potencjału.

3. Gęstość powierzchniowa ładunku i jej związek z natężeniem pola E:

Ładunki elektryczne na powierzchni jakiegoś naładowanego przewodnika rozmieszczone są z różną na ogół gęstością powierzchniowa
. Gęstość powierzchniowa ładunku określamy jako:

(5)

Gdzie:
- ładunek elektryczny znajdujący się na elementarnej powierzchni
.

Ważny jest związek miedzy gęstością powierzchniową ładunku i natężeniem pola elektrycznego, który można zastosować np. do obliczenia wartości
na podstawie znajomości natężenia pola elektrycznego
.

Rozważmy dwie przewodzące płytki, o jednakowych rozmiarach (powierzchnia każdej z płytek wynosi
) ustawione w odległości
od siebie. Przypuśćmy, że na jednej płytce znajduje się ładunek
a na drugiej
, a odpowiednie wartości potencjałów oznaczymy przez
i
.

Zakładając pole jednorodne w całym obszarze między płytkami, odpowiednia gęstość ładunku na wewnętrznej powierzchni jednej z płytek wynosi:

(6)

Gdzie:
- przenikalność elektryczna próżni

2. Stosowane przyrządy:

Układ zawierający dwie płytki kondensatora oraz sondę płomykową, zasilacz wysokiego napięcia WN, woltomierz.

3. Przebieg ćwiczenia:

1. Sprawdzić czy zasilacz WN jest podłączony do sieci.

2. Wyjąć przednią szybę obudowy i ustawić prawą płytkę kondensatora w odległości d₁ = 40mm od przymocowanej płytki.

3. Zapalić sondę płomykową - płomień sondy powinien być jak najmniejszy.

4. Zasunąć przednią szybę.

5. Włączyć zasilacz woltomierza i zasilacz WN.

6. Przesunąć sondę do położenia, przy którym wskazanie woltomierza wynosi około 600V.

7. Przesuwając sondę w kierunku prawej płytki, co 2mm wykonać pomiary potencjału.

8. Wyłączyć zasilacz wysokiego napięcia i rozsunąć okładki na odległość d₂ = 80mm.

9. Powtórzyć czynności pomiarowe jak w punktach e-g, ale pomiary wykonać, co 3mm.

10. Wyłączyć zasilacz wysokiego napięcia i rozsunąć okładki na odległość d₂ = 120mm.

11. Powtórzyć czynności pomiarowe jak w punktach e-g, ale pomiary wykonać, co 3mm.

12. Wyniki pomiarów zestawić w Tab.1.

Tab.1

d=40 [mm]		d=80 [mm]		d=120 [mm]
l [mm]	V1 [V]	l [mm]	V1 [V]	l [mm]	V1 [V]
10	600	21	600	36	600
12	720	24	700	39	660
14	900	27	770	42	700
16	1080	30	920	45	770
18	1260	33	1040	48	850
20	1450	36	1160	51	890
22	1630	39	1280	54	970
24	1850	42	1400	57	1050
26	2030	45	1540	60	1120
28	2220	48	1680	63	1210
30	2390	51	1800	66	1290
32	2590	54	1960	69	1380
34	2740	57	2100	72	1460
36	2910	60	2240	75	1570
38	-	63	2420	78	1660
		66	2580	81	1760
		69	2730	84	1870
		72	2820	87	1950
		75	3000	90	2120
		78	-	93	2180
				96	2290
				99	2360
				102	2500
				105	2610
				108	2740
				111	2850
				114	3000
				117	-

4. Opracowanie wyników pomiarowych / tabele / obliczenia:

a) Na podstawie wyników pomiarów z tab.1 sporządzić trzy wykresy zależności U=f(l), a następnie obliczyć współczynniki a i b prostych regresji dopasowanych do wykreślonych zależności (współczynniki zostały wyliczone i odczytane z programu rysującego funkcje):

d=40mm

a=91,63 ± 0,781 [V/mm]

b=-366,9 ± 19,024 [V]

d=80mm

a=45,2 ± 0,65 [V/mm]

b=-446,6 ± 33 [V]

d=120mm

a=30,85 ± 0,63 [V/mm]

b=-669,1 ± 50 [V]

b) Obliczyć teoretyczne wartości natężenia pola elektrycznego E_t dla poszczególnych wartości d i zadanego napięcia miedzy okładkami (wartość napięcia odczytać z zasilacza WN:

d=40mm

d=80mm

d=120mm

c) Obliczyć względne odchylenia δ (wyrażone w procentach) wartości doświadczalnych natężenia pola elektrycznego E_d od wartości teoretycznych E_t:

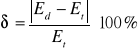
d=40mm

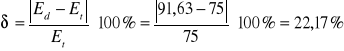
d=80mm

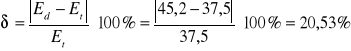
d=120mm

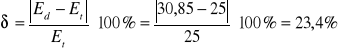
Tab.2.

d1=40mm			d2=80mm			d3=120mm
Ed [V/mm]	Et [V/mm]	δ [%]	Ed [V/mm]	Et [V/mm]	δ [%]	Ed [V/mm]	Et [V/mm]	δ [%]
91,63	75	22,17	45,2	37,5	20,53	30,85	25	23,4

d) Obliczyć gęstości powierzchniowe ładunku
_d na wewnętrznej powierzchni jednej z płytek, na podstawie trzech doświadczalnych zależności U=f(l) wyznaczonych w pkt. a.

d=40mm - zależność liniowa U=f(l) więc:

E_d=91,63 [V/mm]

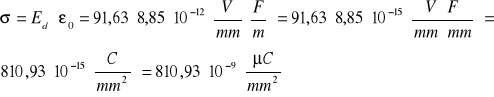
d=80mm - zależność U=f(l) odbiega od prostej więc współczynniki a i b wyznaczamy z kilku ostatnich pomiarowych punktów gdzie widoczna jest lokalna zależność liniowa (współczynniki odczytujemy z programu):

a=49,89 ± 0,89

b=-737,44 ± 57

a=E_dl=49,89[V/mm]

d=120mm - zależność U=f(l) odbiega od prostej, więc postępujemy tak samo jak dla d=80mm:

a=37,11 ± 1,3

b=-1268,7 ± 130

a=E_dl=37,11[V/mm]

Tab.3.

d1=40mm		d2=80mm		d3=120mm
Ed [V/mm]	σ x 10^-7[μC/mm^2]	Edl [V/mm]	σ x 10^-7[μC/mm^2]	Edl [V/mm]	σ x 10^-7[μC/mm^2]
91,63	8,1	49,89	4,4	37,11	3,3

e) Policzyć w 3 przypadkach liczbę elektronów przypadająca na 1 mm² powierzchni płytki:

d=40mm

liczba elektronów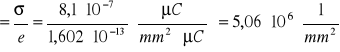

d=80mm

liczba elektronów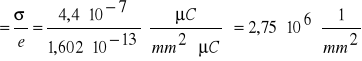

d=120mm

liczba elektronów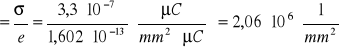

d=40mm	d=80mm	d=120mm
liczba elektronów [1/mm^2]	liczba elektronów [1/mm^2]	liczba elektronów [1/mm^2]
5,06*10^6	2,75*10^6	2,06*10^6

5. Wnioski:

Metoda ta nie jest w 100% skuteczna. Błędy popełnione w trakcie wykonywania tego ćwiczenia są spowodowane małą dokładnością przyrządu pomiarowego (linijka), małą dokładnością odczytów pomiarów oraz indywidualnymi własnościami oka obserwatora. Dodatkowo jest ona dość niebezpieczna gdyż grozi porażeniem prądem o wysokim napięciu.

4

---