Laboratorium Fizyki I

Ćwiczenie nr 36: BADANIE EFEKTU FOTOELEKTRYCZNEGO

ZEWNĘTRZNEGO

1. Wstęp.

Celem ćwiczenia było zapoznanie się z metodą wyznaczenia stałej Plancka, oraz pracy wyjścia elektronu, przy pomocy metody sumy najmniejszych kwadratów. W doświadczeniu tym wielkościami mierzonymi były: V_h przy ustalonym λ.'

2. Układ Pomiarowy.

nanoamperomierz: typ U722A

woltomierz: V534

3. Wykonanie ćwiczenia:

1. Włączenie układu pomiarowego, wyregulowanie położenia 0 w amperomierzu.

2. Dokonanie pomiarów potencjału hamowania dla długości fali światła od 420 do 640nm co 10nm.

3. Zbadanie zależności prądowo - napięciowej fotokomórki, od natężenia = 0nA, do uzyskania napięcia = 12V dla światła o długości 420nm i 640nm. Napięcie było zmieniane w zakresie 0-1nA co 0,04nA, a w pozostałej części zakresu co 0,2nA.

4. Wyniki i ich opracowanie.

Badanie zależności długości światła(częstotliwości) od potencjału hamowania:

Lp.	Długość fali λ [nm]	Potencjał Hamowania Vh [V]	Częstotliwość ν [THz]
1	420	-1,245	713,79
2	430	-1,217	697,19
3	440	-1,118	681,34
4	450	-1,060	666,21
5	460	-1,006	651,72
6	470	-0,949	637,85
7	480	-0,881	624,56
8	490	-0,836	611,82
9	500	-0,778	599,58
10	510	-0,735	587,82
11	520	-0,687	576,52
12	530	-0,644	565,64
13	540	-0,596	555,17
14	550	-0,548	545,07
15	560	-0,500	535,34
16	570	-0,466	525,95
17	580	-0,431	516,88
18	590	-0,399	508,12
19	600	-0,373	499,65
20	610	-0,344	491,46
21	620	-0,346	483,53
22	630	-0,347	475,86
23	640	-0,341	468,42

Częstotliwość wyliczona jest ze wzoru ν=c/λ, gdzie c=prędkość światła (c=299792458 m/s)

Przykładowe wyliczenie dla λ=640nm:

ν=c/λ = 299792458 [m/s] / 6,4*10^-7 [m] = 4,6842*10¹⁴[Hz] = 468,42 [THz]

Aby możliwe było skorzystanie z metody najmniejszych kwadratów należy zasadę zachowania energii dla zderzenia elektronu i fotonu sformułowaną przez Einsteina napisać w następującej postaci:

gdzie h- stała Plancka

ν - częstotliwość światła

e - ładunek elektronu

W-praca wyjścia elektronu

Dzięki zabiegowi linearyzacji funkcji możemy swobodnie zastosować metodę sumy najmniejszych kwadratów do obliczenia szukanych wartości i ich błędów. W zlinearyzowanym równaniu (y=a+bx) rolę b-pełni (h/e), a rolę a- pełni (W/e).

Po zastosowaniu metody sumy najmniejszych kwadratów przy pomocy a i b możemy, znając elementarny ładunek elektronu wyliczyć, wyliczyć stałą Plancka i pracę wyjścia.

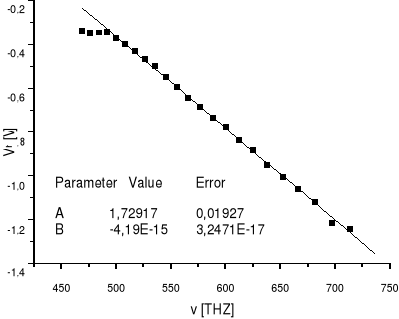
Dopasowanie na wykresie zostało dokonane tylko dla zakresu w którym postać funkcji jest liniowa.

Jak wynika z powyższego wykresu

b = -4,19*10^-15 ± 3,2471*10^-17

a = 1.72917 ± 0,01927

Tak więc mając dany ładunek elektronu e=1,60*10^-19[C] możemy wyliczyć stałą Plancka ze wzoru : h=|b*e|

h=|-4,19*10^-15 * 1,60*10^-19| = 6,704*10^-34 [J*s]

W podobny sposób mając dane e- ładunek elementarny i b- stałą wyliczoną metodą sum najmniejszych kwadratów możemy wyliczyć pracę wyjścia elektronu ze wzoru: W=|a*e|

W=|1,60*10^-19 * 1.72917 | = 2,766672*10^-19 [J]

Błąd w ten sposób wyliczonych wartości wyliczamy w następujący sposób, przy założeniu że wartość elektronu nie jest obarczona błędem:

Δh=Δb*E

Δh= 3,2471*10^-17* 1,60*10^-19 = 0,0519536 *10^-34 [J*s]

ΔW=Δa*e

ΔW=0,01927 * 1,60*10^-19= 3,0832*10^-21 [J] = 0,030832*10^-19 [J]

Jak wynika z powyższych obliczeń wartości obliczane w doświadczeniu mają następującą postać:

h=(6,704±0,052)*10^-34 [J*s]

W=(2,767±0,031)*10^-19 [J] = (1,73±0,02) [eV]

Pracę wyjścia w dżulach przeliczyłem na elektronowolty korzystając z następującej metody:

1[eV] / x [eV] = 1,602*10^-19 [J] / 2,767*10^-19 [J] ->

x = (1 [eV] * 2,767*10^-19 [J] ) / 1,602*10^-19 [J] = 1,73 [eV]

Gdzie x równy jest szukanej pracy wyjścia w elektronowoltach.

Na tej samej zasadzie przeliczyłem błąd pracy wyjścia na elektronowolty.

3. Wnioski:

Wartości które otrzymaliśmy wskutek analizy wyników doświadczenia są bardzo małe, mimo to są porównywalne z danymi tablicowymi (wartość tablicowa h=6,6260755)*10^-34 [J*s]).

Jednoznacznie dowodzi to prawidłowości zastosowanej metody pomiarowej.

Z odszukanych przeze wartości pracy wyjścia dla poszczególnych metali, wynika iż metalem z którego wykonana jest fotokatoda jest cez.

W celu uzyskania dokładniejszych wyników należałoby zastosować urządzenia o mniejszym błędzie systematycznym. Należałoby również zapewnić lepsze warunki do przeprowadzenia pomiarów dla tak czułego urządzenia jak nanoamperomierz.

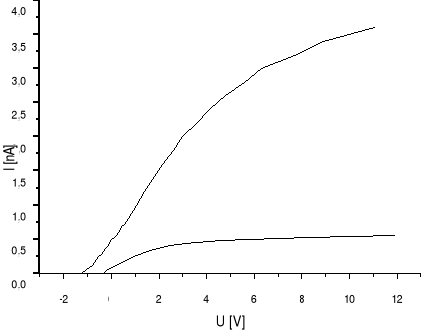
Poniżej załączam wykres zależności prądowo-napięciowej dla światła o długości 640nm i 420nm:

---