Wydział EAIiE

kierunek Automatyka i Robotyka

wykonanie ćwiczenia - 19.12.2007

Andrzej Leśko grupa laboratoryjna 4

Rozwiązywanie układów równań liniowych

1. Wstęp

Rozpatrujemy układy równań liniowych postaci Ax=B, gdzie A jest pewną macierzą (posiadającą m wierszy i n kolumn), B jest znanym wektorem (posiadającym m współrzędnych), a x jest szukanym wektorem (n nieznanych współrzędnych).

Układy takie mogą mieć 0, 1 lub nieskończenie wiele rozwiązań. Ilość rozwiązań można przewidzieć analizując odpowiednie - zazwyczaj dość proste warunki.

Rozwiązanie omawianych układów można znaleźć na wiele różnych sposobów, które generalnie można podzielić na dwie grupy: metody dokładne i metody iteracyjne.

Metody dokładne (np. metoda Cramera, eliminacji Gaussa, rozkładu LU) - pozwalają przy wykorzystaniu skończonej ilości dokładnych działań arytmetycznych, przekształcających macierz A i wektor B, otrzymać rozwiązanie.

Metody iteracyjne (np. metoda Jacobiego, metoda Gaussa-Seidla) - polegają na wykonaniu skończonej ilości działań, coraz lepiej przybliżających rozwiązanie. Za pomocą tych metod - zwiększając ilość obliczeń możemy znaleźć wynik z dowolną dokładnością.

Aby dana metoda iteracyjna mogła przynieść oczekiwany efekt - muszą być spełnione odpowiednie - zależne od wyboru metody warunki zbieżności.

2. Wykonanie ćwiczenia

1. Metody dokładne - metoda Cramera

Metoda Cramera pozwala znaleźć rozwiązanie układu równań poprzez obliczanie ilorazów wyznaczników odpowiednich macierzy.

Najpierw obliczamy wyznacznik główny - wyznacznik macierzy A.

Następnie kolejne j-te kolumny macierzy zastępujemy znanym wektorem B i obliczamy wyznaczniki tak otrzymanych macierzy. Rozwiązaniem układu jest wektor składający się z j wyznaczników tych macierzy podzielonych przez wyznacznik główny.

Gdy wyznacznik główny jest niezerowy - układ posiada jedno rozwiązanie. Gdy wyznacznik główny jest zerowy i pozostałe j wyznaczników też jest równa 0 - układ ma nieskończenie wiele rozwiązań. W przeciwnym razie układ jest sprzeczny.

Dany był układ równań:

Ax=b

gdzie:

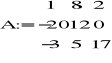
Układ rozwiązałem za pomocą funkcji:

- ta funkcja tworzyła odpowiednie macierze - gdzie i- ta kolumna zastępowana jest wektorem b i zwracała wyznacznik macierzy

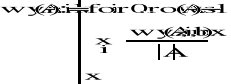
- druga funkcja wykonywała odpowiednie dzielenia i w efekcie znajdowała rozwiązanie.

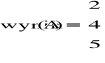
- wynik - rozwiązanie badanego układu równań

2. Metody dokładne - metoda eliminacji Gaussa

Metoda eliminacji Gaussa składa się z dwóch etapów.

W pierwszym wykonujemy odpowiednie operacja na wierszach macierzy A i wektora b tak, aby przekształcić macierz do macierzy trójkątnej górnej.

W drugim etapie korzystając z odpowiedniego wzoru rekurencyjnego wyznaczamy niewiadome - zaczynając od ostatniej, stąd etap ten nazywamy postępowaniem odwrotnym.

Etap pierwszy:

Aby otrzymać macierz trójkątną musimy kilkakrotnie powtórzyć następujące działanie:

od i-tego wiersza układu odejmujemy wiersz pierwszy pomnożony przez iloraz współczynników - pierwszy współczynnik pierwszego wiersza podzielony przez pierwszy współczynnik i-tego wiersza. Oczywiście analogiczną operacją wykonujemy na wektorze b.

W pierwszej iteracji uzyskamy zera na pierwszej pozycji każdego wiersza (poza pierwszym). Analogicznie eliminujemy niezerowe wartości na kolejnych pozycjach - od i-tego wiersza odejmujemy w kolejnych iteracjach pomnożone przez odpowiedni iloraz kolejne wiersze: 2,3,…,n.

Otrzymujemy macierz trójkątną górną.

Etap drugi:

Ostatnią współrzędną szukanego wektora x otrzymujemy wprost - dzieląc ostatnią współrzędną wektora b przez jedyny wyraz ostatniego wiersza macierzy trójkątnej.

Z tak otrzymanym wynikiem przesuwamy się „wyżej” - obliczamy przedostatnią współrzędną wektora x. Wykorzystujemy wzór rekurencyjny:

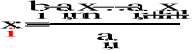
Dane były:

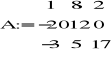
Do rozwiązanie układu równań (tego samego co w przypadku metody Cramera) metodą eliminacji Gaussa wykorzystałem funkcje:

n - indeks ostatniej kolumny i wiersza, bo macierz jest kwadratowa

k - mówi który wiersz traktujemy jako bazowy - względem którego liczymy

i - to numer wiersza. skoro bazowy jest k-ty to zaczynamy liczyć na k+1

s - to iloczyn prze który będziemy mnożyć każdy wiersz

wykonujemy odpowiednie iteracje na macierzy b i A

j - numer kolumny - liczymy po wszystkich kolumnach od k do n

dopisujemy wektor wyników b do macierzy A

Funkcja Gauss1 tworzy macierz trójkątną górną.

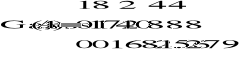
Ostatnia kolumna macierzy to wektor b.

Funkcja Gauss2 rozwiązuje macierz trójkątną i zwraca szukany wektor x:

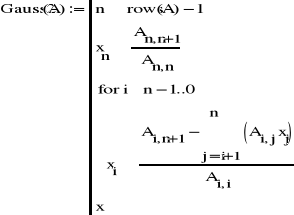
- wyznaczamy ostatnią współrzędna szukanego wektora

- realizacja wzoru rekurencyjnego

Otrzymałem wynik:

3. Metody dokładne - metoda rozkładu LU

W metodzie tej poszukujemy macierzy trójkątnych L i U, których iloczyn będzie równy danej macierzy A. Macierze L (trójkątna dolna) i U (trójkątna górna) można wyznaczyć korzystając z algorytmów związanych z metodą eliminacji Gaussa.

Macierz U wyznaczyłem korzystając z funkcji:

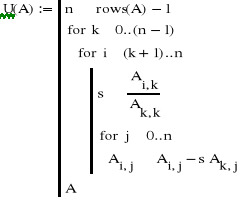
Funkcja ta tylko nieznacznie różni się od funkcji Gauss1 (różnica polega na opuszczeniu obliczeń związanych z wektorem b).

Macierz L wyznaczyłem korzystając z funkcji:

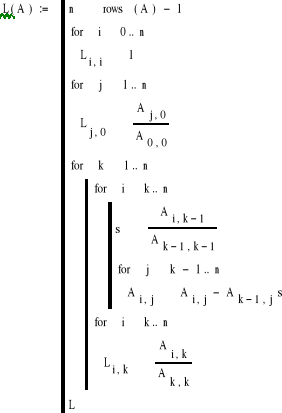
Celem tej funkcji było znalezienie macierzy postaci:

gdzie L - to iloraz odpowiednich współczynników początków wierszy macierzy A - otrzymanych w kolejnych iteracjach (L z pierwszej kolumny - współczynniki z pierwszej iteracji, L drugiej kolumny - to współczynniki z drugiej iteracji itd.)

Tak jak poprzednio:

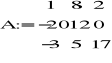
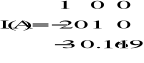
Zatem wykonując obliczenia otrzymałem:

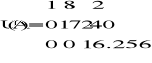
oraz

Rzeczywiście:

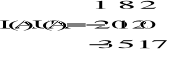
zatem macierze L i U zostały wyznaczone poprawnie.

Kolejnym krokiem metody jest rozwiązanie układów równań:

Ly=b oraz Ux=Y (ponieważ Ax=b oraz LU=A)

Macierz L - jest macierzą trójkątną dolną, zatem układ równań łatwo rozwiązać - począwszy od pierwszego wiersza, a następnie rekurencyjnie obliczając niewiadome z kolejnych wierszy:

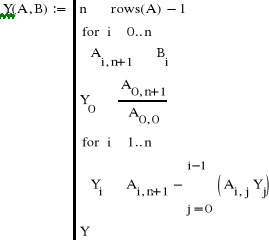
-do macierzy A dopisujemy dodatkową kolumnę - wektor B

-pierwsza niewiadoma

-wzór rekurencyjny

- zwracam wektor Y

Mając wektor Y - możemy rozwiązać drugi układ. Można do tego wykorzystać funkcję Gauss2 - ponieważ mamy układ z macierzą trójkątną górną.

Musimy jednak do macierzy U dodać dodatkowy wektor - Y (ponieważ macierz takiej postaci jest argumentem mojej funkcji Gauss2)

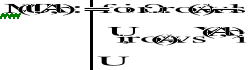
-dodanie do macierzy trójkątnej wektora Y

Otrzymujemy macierz:

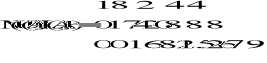
ponieważ wektor Y był postaci:

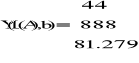
Podstawiając macierz do funkcji Gauss2 otrzymujemy:

Co jest poprawnym rozwiązaniem naszego układu.

Funkcja niekorzystająca z funkcji Gauss2 byłaby postaci:

dołączenie wektora B do macierzy trójkątnej A

obliczenie ostatniej współrzędnej szukanego wektora

wzór rekurencyjny - identyczny ze wzorem z funkcji Gauss2

A wynik zgodnie z oczekiwaniami:

4. Metody iteracyjne - macierze L, U, D

W przypadku dwóch rozpatrywanych na ćwiczeniach metod iteracyjnych - metodzie Jacobiego i metodzie Gaussa-Seidla - macierz A układu równań Ax=b musi być taką macierzą, aby można było ją rozłożyć na macierze: diagonalną (D), poddiagonalną (L) oraz naddiagonalną (U).

W ćwiczeniu rozpatrywałem układ równań, w którym:

Można było zatem łatwo wyznaczyć macierz L, U, D. Wykorzystałem następujące funkcje:

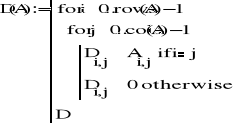
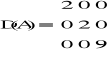
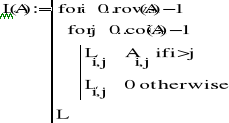
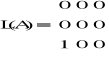
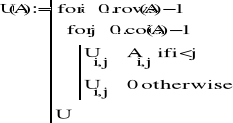
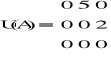
Z macierzy L, U, D tworzymy następnie kolejną macierz - będącą punktem wyjścia do dalszych kroków metod:

- dla metody Jacobiego tworzymy macierz:

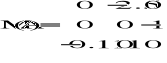
- dla metody Gaussa-Seidla macierz:

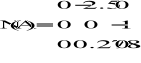
5. Metody iteracyjne - warunki zbieżności

Aby metody iteracyjne mogły zostać zastosowane muszą spełnione być pewne warunki gwarantujące, że dany algorytm doprowadzi nas do rozwiązania.

Warunek zbieżności dla metod jest następujący: promień spektralny macierzy M (lub N) musi być mniejszy od 1 (Promień spektralny to największa co do modułu wartość własna danej macierzy).

Aby sprawdzić czy w przypadku danej macierzy A mogę stosować omawiane metody obliczyłem promienie spektralne wyznaczonych w poprzednim kroku macierzy M i N. W tym celu wykorzystałem następujące funkcje zwracające wektor wartości własnych:

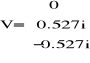
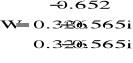
Oraz funkcję obliczającą moduł wartości własnych:

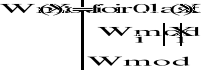
Oraz funkcję znajdującą największą współrzędną w danym wektorze:

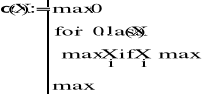
Przekazując tej funkcji wektor modułów wartości własnych wyznaczałem promień spektralny macierzy.

Dla metody Jacobiego - i macierzy M(A) - promień spektralny wyniósł:

Dla metody Gaussa-Seidla:

Zatem w obydwu przypadkach warunki zbieżności były spełnione - można było kontynuować obliczenia.

6. Metody iteracyjne - metoda Jacobiego i metoda Gaussa-Seidla - kroki iteracyjne

Iterację w obydwu metodach rozpoczyna się przyjmując pewne - dowolne wartości początkowe, które automatycznie stają się pierwszym przybliżeniem szukanego wektora x. Dla obydwu metod przyjąłem jako wartości początkowe wektor o zerowych współrzędnych.

Związek między kolejnymi iteracjami można zapisać - dla metody Jacobiego:

Co można zapisać:

Natomiast dla metody Gaussa-Seidla:

A zapisując dla współczynników macierzy:

Wyniki każdej kolejnej iteracji dołączałem do danego wektora startowego - tworząc w ten sposób macierz o coraz większej - równej ilości iteracji - liczbie kolumn.

Napisałem następujące funkcje rozwiązujące układ równań:

Metoda Jacobiego (wyniki kolejnych iteracji zapisane w macierzy Ja):

ustalenie wartości początkowych

pętla for - zabezpiecza przed nieskończonymi obliczeniami - możliwymi w razie błędu implementacji

właściwe obliczenia - pozwalające na wyznaczenie kolejnego przybliżenia wyniku - wykorzystując przybliżenie poprzednie

pętlę przerywamy, gdy różnica między kolejnymi przybliżeniami będzie wystarczająco mała

funkcja zwraca wynik ostatniej iteracji

dodatkowa współrzędna zwracanego wektora informuje o ilości wykonanych iteracji

Metoda Gaussa-Seidla (wyniki kolejnych iteracji w macierzy GS):

Funkcja realizująca metodę Gaussa-Seidla różni się jedynie sposobem obliczania kolejnego przybliżenia:

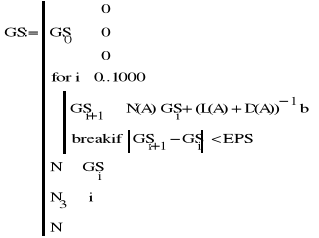
wzór rekurencyjny - jedyna różnica między funkcjami realizującymi metody Jacobiego i Gaussa-Seidla

Przyjmując

Otrzymałem wyniki:

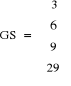
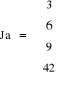
Zatem obie metody pozwoliły znaleźć rozwiązanie danego układu.

3. Wnioski

1. Metoda Cramera wymaga (n+1)! mnożeń, zatem warto ją stosować tylko przy niedużych macierzach - gdy znalezienie wyznaczników nie wymaga wielu obliczeń. Metoda Eliminacji Gaussa wymaga wykonania

mnożeń oraz dodawań

Zatem przy większych macierzach stosuje się metodę eliminacji Gaussa. Metoda rozkładu LU wymaga:

mnożeń oraz dodawań

Jest zatem jeszcze mniej kosztowna od metody eliminacji Gaussa.

2. Gdy do rozwiązania mamy kilka układów różniących się tylko wektorem b to najkorzystniejsza jest metoda rozkładu LU, ponieważ w takim przypadku wystarczy jednorazowe wyznaczenie macierzy L oraz U. Dzięki temu liczba niezbędnych działań do rozwiązania kolejnych układów będzie jeszcze mniejsza.

3. Aby stosować metody iteracyjne koniecznie należy sprawdzić warunki zbieżności. Metodę Gaussa-Seidla można stosować jedynie, gdy na diagonalni są elementy niezerowe.

Obie metody są zbieżne, gdy dana macierz A jest silnie diagonalnie dominująca wierszowo lub kolumnowo.

Jeśli macierz A jest symetryczna i dodatnio określona to zbieżna jest metoda Gaussa-Seidla, natomiast metoda Jacobiego nie musi być zbieżna.

4. Metoda Gaussa-Seidla pozwoliła znaleźć rozwiązanie po znacznie mniejszej liczbie obliczeń niż metoda Jacobiego. Zatem jeśli tylko warunki zbieżności są spełnione warto wybrać metodę Gaussa-Seidla, gdyż jest ona szybciej zbieżna.

19.12.2007

Andrzej Leśko grupa 4

---