Wydział Elektroniki Politechniki Wrocławskiej	Laboratorium Przyrządów Półprzewodnikowych
^Wykonał		^Grupa -	^Ćw. nr 4	^Prowadzący
Wpływ temperatury na półprzewodnik (termistory) oraz na złącze p - n		^Data wykonania	^Data oddania	^Ocena

WYKAZ PRZYRZĄDÓW :

• Multimetr cyfrowy 1331

• Multimetr cyfrowy VC-10T

• Piec KBC II

• Termistor NTC

• Tranzystor TG-5

PRZEBIEG ĆWICZENIA :

1. Pomiar charakterystyki rezystancyjno - temperaturowej termistora

Rys. 1. Schemat do wyznaczania charakterystyki R_T = f(T) termistora

Piecyk wraz z termistorem nagrzano do temperatury 90°C, wyłączono grzałkę piecyka i mierzono charaktery­stykę w czasie studzenia. Wyniki pomiarów zamieszczono w tabeli:

T	T	1/T	RT
[ °C ]	[ K ]	[ 1/K ]	[ kΩ ]
22	295	0,00339	6,880
90	363	0,00275	0,251
85	358	0,00279	0,334
80	353	0,00283	0,443
75	348	0,00287	0,575
70	343	0,00292	0,766
65	338	0,00296	1,002
60	333	0,00300	1,307
55	328	0,00305	1,651
50	323	0,00310	2,085
45	318	0,00314	2,698
40	313	0,00319	3,570
35	308	0,00325	4,540

Charakterystyka R_T = f(1/T) przedstawiona jest na wykresie 1.

Wzory i obliczenia:

a) Wyznaczenie R_∞

Ponieważ z wykresu 1, zamieszczonego na papierze półlogarytmicznym, nie można odczytać wartość R_∞ (ze względu na małe jej wartości) dlatego posłużę się wykresem komputerowym. Na rys. 2 przedstawiono również charakterystykę R_T = f(1/T) wraz z równaniem prostej (krzywej logarytmicznej, ponieważ oś rzędnych zlogaryt­mowano), która określa zależność rezystancji termistora od temperatury. Zależność ta jest określona wzorem:

.

Z równania zamieszczonego na wykresie:

możemy odczytać, że wartość rezystancji R_∞ wynosi 0,1035819⋅10^-6 kΩ = 103,5819 nΩ.

Czyli ostatecznie R_∞ = 103,5819 [nΩ].

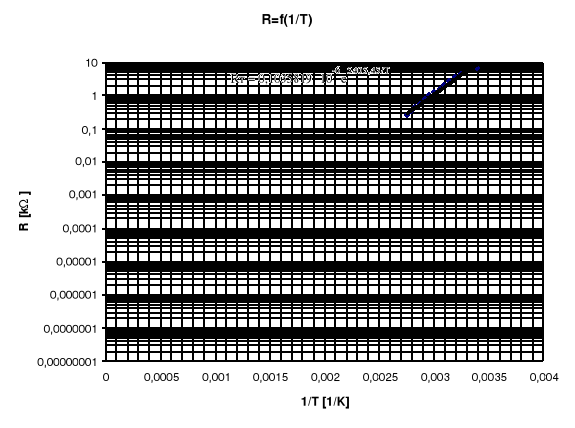
Rys. 2. Charakterystyka RT = f(1/T) termistora NTC

b) Wyznaczenie stałej materiałowej B

W celu wyprowadzenia wzoru na B skorzystamy z zależności rezystancji termistora od temperatury. Ponadto z prostoliniowego odcinka charakterystyki weźmiemy dwa punkty o odpowiednich współrzędnych (1/T₁, R_T1) i (1/T₂, R_T2). Zależność rezystancji od temperatury dla termistora ma postać:

.

Dla punktów z charakterystyki wzór ten będzie miał postać:

.

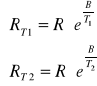
Logarytmując powyższe wzory otrzymujemy:

.

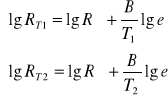
Następnie odejmując od równania drugiego równanie pierwsze otrzymamy:

.

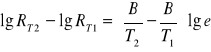
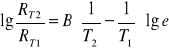
Po czym otrzymujemy ostatecznie wzór na B:

.

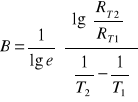
Do obliczeń przyjmuję następujące punkty:

R_T1 = 0,4 [kΩ], 1/T₁ = 2,824⋅10^-3 [1/K]

R_T2 = 4,0 [kΩ], 1/T₂ = 3,250⋅10^-3 [1/K]

i otrzymuję stałą materiałową B równą:

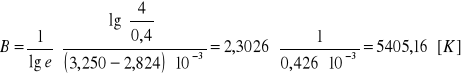
Czyli ostatecznie B = 5405,16 [K].

Posługując się, tak jak przy wyznaczaniu rezystancji R_∞, wykresem komputerowym i otrzymanym wzorem widzimy, że otrzymaliśmy ten sam wynik (B odczytane z wykresu wynosi 5405,45). Małe różnice otrzymane w dziesiątych częściach wynikają z niedokładności odczytania danych z wykresu.

c) Wyznaczenie temperaturowego współczynnika rezystancji α_T w temperaturze otoczenia (22 °C)

W celu wyprowadzenia wzoru na temperaturowy współczynnik rezystancji α_T skorzystamy z zależności rezystancji termistora od temperatury i definicji α_T:

, gdzie

Otrzymujemy zatem, że

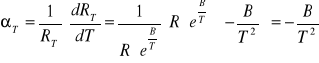
Dla temperatury otoczenia 22 °C (295 K) otrzymujemy:

Czyli ostatecznie α₂₉₅ = -0,062 [1/K] = -6,2 %/K.

2. Pomiar wpływu temperatury na złącze p - n

Rys. 3. Schemat do badania wpływu temperatury na złącze p - n:

1 - polaryzacja w kierunku zaporowym

2 - polaryzacja w kierunku przewodzenia

Do wyznaczania wpływu temperatury na złącze p-n użyto tranzystora germanowego p-n-p TG-5. Jako złącze p-n wykorzystano kolektor i bazę tranzystora. Piecyk nagrzano do temperatury 70°C, a następnie w czasie studzenia mierzono prąd dla kierunku zaporowego na przemian z napięciem dla kierunku przewodzenia. Wyniki pomiarów zamieszczono w tabeli:

T	T	1/T	I	U
[ °C ]	[ K ]	[ 1/K ]	[ mA ]	[ V ]
70	343	0,00292	1,116	0,0323
65	338	0,00296	0,536	0,0397
60	333	0,00300	0,232	0,0435
55	328	0,00305	0,117	0,0471
50	323	0,00310	0,058	0,0501
45	318	0,00314	0,028	0,0523

Na wykresie 2 przedstawiono charakterystykę lg I = f(1/T) dla kierunku zaporowego, zaś na wykresie 3 i 4 charakterystykę U = f(T) dla kierunku przewodzenia.

Wzory i obliczenia:

1. Charakterystyka lg I = f(1/T)

a) Wyznaczenie szerokości pasma zabronionego W_g

W celu wyprowadzenia wzoru na szerokość pasma zabronionego W_g skorzystamy z uproszczonego wzoru na prąd nasycenia (taki prąd płynie w złączu germanowym w kierunku zaporowym). Ponadto z prostoliniowego odcinka charakterystyki weźmiemy dwa punkty o odpowiednich współrzędnych (1/T₁, I₁) i (1/T₂, I₂). Zależność prądu nasycenia od temperatury ma postać:

.

Dla punktów z charakterystyki wzór ten będzie miał postać:

.

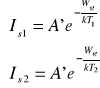
Logarytmując powyższe wzory otrzymujemy:

.

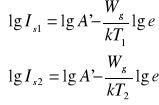
Następnie odejmując od równania pierwszego równanie drugie otrzymamy:

.

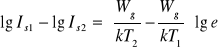
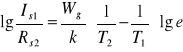
Po czym otrzymujemy ostatecznie wzór na W_g:

.

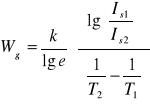
Do obliczeń przyjmuję następujące punkty:

I_s1 = 1 [mA], 1/T₁ = 2,92⋅10^-3 [1/K], I_s2 = 0,03 [mA], 1/T₂ = 3,14⋅10^-3 [1/K]

i otrzymuję szerokość pasma zabronionego równą:

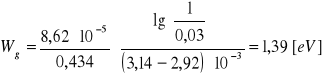
Czyli ostatecznie Wg = 1,39 [eV].

b) Wyznaczenie temperaturowego współczynnika prądu:

Temperaturowy współczynnik prądu wyznacza się na podstawie wzoru na prąd nasycenia:

.

Zatem temperaturowy współczynnik prądu określony jest wzorem:

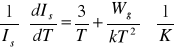
Dla temperatury otoczenia 22°C (295K) mamy:

2. Charakterystyka U = f(T)

Zależność napięcia od temperatury w kierunku przewodzenia ma postać:

.

Wynika ona z uproszczonego wzoru na prąd w kierunku przewodzenia:

.

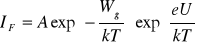
a) Wyznaczenie szerokości pasma zabronionego Wg

Z wykresu U = f(T) oraz z powyższej zależności napięcia od temperatury widzimy, że dla T = 0 K wartość napięcia jest równa szerokości pasma zabronionego przez ładunek elementarny W_g/e [V]. Mnożąc ten iloraz przez ładunek elementarny otrzymamy szerokość pasma zabronionego w elektronowoltach. Zatem wartość napięcia dla T = 0 jest szerokością pasma w eV.

Ze względu na dużą wartość U(0) wykres wykonano komputerowo. Równanie prostej zamieszczone na wykresie 3:

określa zależność napięcia od temperatury dla danych zamieszczonych w tabeli pomiarowej. Z równanie tego widzimy, że dla T = 0 K funkcja przyjmuje wartość 0,3117. Zatem szerokość pasma zabronionego wynosi 0,3117 eV. Dla porównania na wykresie 4 wyznaczono tę wartość. Widzimy, że pokrywa się ona z wartością otrzymaną z równania.

Zatem ostatecznie szerokość pasma zabronionego wynosi W_g = 0,3117 eV.

b) Wyznaczenie temperaturowego współczynnika napięcia:

Temperaturowy współczynnik napięcia określa się wzorem:

Wartość ta jest współczynnikiem kierunkowym prostej w układzie U-T. Zatem z zależności napięcia od temperatury zamieszczonej na wykresie:

widzimy, że temperaturowy współczynnik napięcia wynosi -0,8 mV/°C.

Ostatecznie dU/dT = -0,8 mV/°C.

WNIOSKI I UWAGI:

W pkt. 1 ćwiczenia badaliśmy zależność rezystancji termistora NTC (o ujemnym temperaturowym współczyn­niku rezystancji). Z charakterystyki R = f(1/T) widzimy, że wraz ze wzrostem temperatury rezystancja termistora maleje. Szybkość zmian określa nam stała materiałowa B, której wartość wynosi 5405,45 K. W celu wyznaczenia teoretycznej wartości rezystancji w temperaturze równej nieskończoność R_∞ posłużyłem się analizą komputerową. Z obliczeń widać, że R_∞ jest bardzo mała (setki nanoomów). Oznacza to, że dla temperatury nieskończoność istnieje pewna wartość rezy­stancji, co prawda bardzo mała, ale wartość rezystancji zależy wykładniczo od temperatury i stromo maleje. Temperatu­rowy współczynnik rezystancji dla temperatury pokojowej wyniósł -6,2%/K, co może być porównywalne z rzeczywistą wartością równą -7%/K dla krzemu.

W pkt. 2 ćwiczenia badaliśmy zależność prądu w kierunku zaporowym i napięcia w kierunku przewodzenia od temperatury złącza germanowego (złącze B - C tranzystora). Z charakterystyki lg I = f(1/T) widzimy, że wartość prądu wzrasta wraz ze wzrostem temperatury. Szerokość pasma zabronionego wyznaczona na podstawie tego wykresu wyniosła 1,39 eV. W porównaniu z wartością teoretyczną (0,7 eV) otrzymany wynik jest prawie dwukrotnie zawyżony. Wynikać to może z faktu, że wzór na W_g był wyznaczany przy pewnych uproszczeniach. Teoretycznie w złączu germanowym spola­ryzowanym w kierunku zaporowym płynie tylko prąd nasycenia. Jednak istnieje pewien prąd generacji, rezystancja upływu, które w pewien sposób wpływają na charakterystykę. Podkreślić trzeba, że do obliczeń wykorzystywany był wzór przybliżony. Temperaturowy współczynnik prądu _T wyszedł prawie dwa razy większy od teoretycznego (10%/K). Gdyby przyjąć rzeczywistą wartość szerokości pasma zabronionego (0,7 eV) otrzymalibyśmy rzeczywistą wartość _T.

Z charakterystyki U=f(T) wynika, że wraz ze wzrostem temperatury maleje wartość napięcia na diodzie. Ze względu na to, że pomiary wykonywane były dla małego zakresu zmian temperatury wykres wykonano komputerowo, a do wyzna­czenia szerokości pasma zabronionego i temperaturowego współczynnika napięcia skorzystano z uśrednionej zależności, określającej wartość napięcia na diodzie w kierunku przewodzenia od temperatury. Obliczona szerokość pasma zabronio­nego (0,312 eV) nie pokrywa się całkowicie z wartością teoretyczną, jak również z pomiarami wykonanymi dla kierunku zaporowego. Podobnie rzecz się ma ze współczynnikiem temperaturowym napięcia, który wyszedł ponad dwukrotnie mniejszy niż wartość teoretyczna (-2mV/K). Wartości te wyznaczano z uproszczonego wzoru, w którym przyjęto, że współczynnik doskonałości wynosi 1, a więc w złączu germanowym płynie sam prąd dyfuzyjny, bez uwzględnienia prądu rekombinacji. Jednak przy wyznaczaniu charakterystyki I-U germanowego złącza p-n wykonywanego na drugich zajęciach widać, że tam współczynnik doskonałości wychodził rzędu 1,5. Być może dlatego otrzymaliśmy wyniki obarczone takimi błędami.

- 1 -

---