GRUPA NR: 22 ZESPÓŁ: 3	ĆWICZENIE NR: 3 Prężność pary (sprawozdanie końcowe)	DATA WYKONANIA ĆWICZENIA: 02.06.2008 r.
ZESPÓŁ: 1. Katarzyna Góral 2. Joanna Grzywacz 3. Karolina Paśko 4. Kinga Poźniak			OCENA

1. Wstęp teoretyczny

Prężność pary jest to ciśnienie, pod którym ciecz i para współistnieją w stanie równowagi dynamicznej stanowiąc wówczas układ jednoskładnikowy dwufazowy, który zgodnie z regułą faz Gibbsa posiada         1 stopień swobody (F=C-P Oznacza to, że spośród ekstensywnych parametrów stanu jakimi są np. T,P tylko jeden stanowi zmienną niezależną drugi pozostaje jej funkcją.

Zależność funkcyjna T(P) lub P(T) nazywana jest krzywą równowagi fazowej, a jej opis przedstawia równanie Clapeyrona, które dla omawianego układu równowagowego ciecz-para przybiera postać:

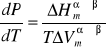
Gdzie:

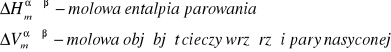
Wymienione wyżej wielkości są, indywidualnymi dla każdej substancji, funkcjami ciśnienia i temperatury, co praktycznie wyklucza scałkowanie równania Clapeyrona w sposób ogólny. Z tego powodu całkuje się, przyjmując następujące założenia upraszczające:

 zakłada się, że objętość molowa cieczy jest znacznie mniejsza od objętości molowej pary nasyconej

 przyjmuje się ze para nasycona jest gazem doskonałym

 pomija się wpływ temperatury i ciśnienia na entalpię parowania i zastępuje ją wartością średnią

 

Przy takich założeniach równanie Clapeyrona przybiera postać:

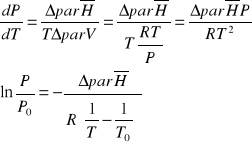
Powyższe równanie można przekształcić do postaci opisującej wpływ ciśnienia na temperaturę wrzenia cieczy

 

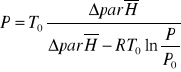
Jak również podać jego ogólną postać

Analiza powyższych zależności wskazuje na istnienie dwóch prawidłowości:

 prężność pary nasyconej cieczy jest monotonicznie rosnącą funkcją temperatury (temperatura wrzenia jest monotonicznie rosnącą funkcją ciśnienia)



 jest praktycznie funkcją liniową o współczynniku nachylenia równym -

.    

2. Cel ćwiczenia

Celem ćwiczenia jest wyznaczenie zależności prężności pary nad wrzącą cieczą w funkcji temperatury, dla n-oktanu, oraz określenie molowej entalpii parowania n-oktanu.

3. Zadane parametry

Dany jest n-oktan o czystości cz.d.a. Należy wyznaczyć prężność pary nad wrzącą cieczą metodą izoteniskopową, dla przedziału temperatur od 30 do 62 stopni Celsjusza, z odstępami 8-stopniowymi. Na podstawie tych danych należy sporządzić wykres zależności prężności pary od temperatury i wykres zależności logarytmu naturalnego prężności pary od odwrotności temperatury. Następnie należy obliczyć molową entalpię parowania (w oparciu o wykres) i porównać wynik z wartością tabelaryczną.

4. Sposób wykonania ćwiczenia

1. Przygotowanie aparatury - zabezpieczenie kranów, uruchomienie pompy próżniowej i ustabilizowanie temperatury w termostacie.

2. Przygotowanie cieczy poddawanej destylacji, uszczelnienie szkła, uruchomienie aparatury.

3. Doprowadzenie cieczy do wrzenia, zamknięcie dostępu powietrza.

4. Otworzenie dwóch kranów w celu wyciągnięcia cieczy wrzącej ponad izoteniskop.

5. Zmiana otwarcia kranów w celu ustabilizowania poziomu cieczy.

6. Wyrównanie poziomu cieczy w izoteniskopie i utrzymywanie go przez pewien okres czasu.

7. Odczytanie różnicy temperatur na manometrze rtęciowym.

8. Odgazowanie układu badawczego i przygotowanie go do kolejnego pomiaru, powtórzenie pomiaru.

Takiego zestawu pomiarów dokonuje się następnie dla wyższych temperatur. Należy uważać przy tym, aby względna różnica pomiędzy dwoma kolejnymi pomiarami (w identycznej temperaturze) nie przekroczyła 5 %.

5. Wyniki pomiarów

	Numer pomiaru	Temperatura, w której dokonano pomiaru		Prężność pary (po 3 pomiary w każdej temperaturze), [mm Hg]			Średnia prężność pary w danej temperaturze
			[°C]				[K]				[mm Hg]	[Pa]
Zespół nr 1	1		293	27	23	26 i 22	22,50	3263,6
		2		313	43	45	41 i 42	42,75	5694,7
		3		327	73	76	74 i 75	74,5	9924,1
		4		334	98	102	100 i 101	100,25	13354,1
	Zespół nr 2	1		306	21	20	21	20,67	2755,27
		2		313	29	27	28	28	3733,03
		3		320	40	42	42	41,3	5506,21
		4		327	52	52	53	52,3	6972,76
	Zespół nr 3	1	30	303	1	1	1	1	133,3
		2	38	311	1	1	1,5	1,2	160
		3	46	319	2	1,5	2,5	2	266,7
		4	54	327	3	3	2	2,7	360
	Zespół nr 4	1		302	16	8	8	10,6	2480
		2		309	14,5	14	13,5	14,2	3413,33
		3		318	26	28	26	26,6	4533,33
		4		328	45	44	45	44,7	5280
	Zespół nr 5	1		304	16	18		17	2266,47
		2		311	24	22		23	3066,41
		3		318	39	45	37	40,34	5378,21
		4		325	59	54	48	53,67	7155,5
	Zespół nr 6	1		303	8	9		8,5
		2		313	12	12		12
		3		323	15	14		14,5
		4		333	20	21		20,5
		5		343	23	23		23

Nr zespołu	Wartość ΔH
1	27,44
2	26,4
3	35,75
4	43,624
5	47,096
6	21,889

6.Przykładowe opracowanie danych doświadczalnych

Obliczamy entalpię parowania oktanu.

Wiemy, że:

Co możemy również zapisać:

Iloraz znajdujący się po lewej stronie równania jest tangensem kąta nachylenia prostej dopasowania (naszego wykresu) do osi x, czyli zarazem współczynnikiem kierunkowym tej prostej:

Zatem lewa strona równania jest równa:

Mając zależność:

a=-ΔH/R

przekształcamy ją, tak aby wyliczyć ΔH:

ΔH=-a*R

Współczynnik kierunkowy a określony na podstawie drugiego wykresu wynosi:

a=(-4,3+-0,7)*10^3

czyli a=-4300

Wiemy że R=8,314

Podstawiając do wzoru:

ΔH=-(-4300)*8,314

Mamy, że:

ΔH=35750,2[J]=35,75[kJ]

Tabelaryczna wartość molowej entalpii parowania n-oktanu w temperaturze wrzenia wynosi:

ΔHt=34,4[kJ/mol]

Błąd naszego pomiaru wynosi:

Δx=( ΔH- ΔHt)*100%/ ΔHt

Δx=(35,75-34,4)*100%/34.4=3,9%

7. Dyskusja wyników

Obliczanie przedziału ufności

Stosując rozkład Studenta-Fischera przedział ufności zakładamy na poziomie p=0,95 i obliczamy ze wzoru:

τ- wartość współczynnika rozkładu t-Studenta zależną od liczby oznaczeń n i poziomu ufności p

S - odchylenie standardowe

- odchylenie standardowe średniej

n - liczba pomiarów

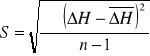
ΔH - pomiar entalpii

- średnia entalpia

Regresja prostoliniowa

8.Wnioski końcowe

Na podstawie wyników doświadczeń wszystkich zespołów otrzymano entalpie parowania

n-oktanu o wartości ΔH_par=31,6 [kJ], zbliżona do wartości tablicowej. Przy rysowaniu wykresu nie uwzględniłyśmy wyników 2 zespołów 3 i 6 ponieważ były obarczone znacznym błędem. W celu zbadania błędów naszych pomiarów wykreśliłyśmy wykres dla funkcji
, która umożliwiła nam odrzucenie wyników najbardziej odbiegających od tablicowych wartości.

Źródłami błędów mogły być:

• Nieszczelność aparatury

• Zanieczyszczenie układu

• Błędy podczas odczytywania ciśnienia na manometrze rtęciowym

• Wahania ciśnienia zewnętrznego

• Inne błędy przypadkowe popełniane przez różne osoby przeprowadzające doświadczenie

---