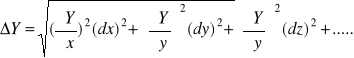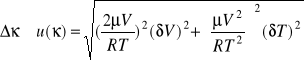Tekst przygotowany częściowo w oparciu o opis Ćwiczenia 0: „Szacowanie niepewności w pomiarach laboratoryjnych”, J. Ostachowicz, Zeszyt A1 do ćwiczeń laboratoryjnych z fizyki, Wydział Fizyki i Informatyki Stosowanej. Pełny tekst, a także opisy większości ćwiczeń znajdują się w Zeszycie: http://www.ftj.agh.edu.pl/zdf/zeszyt.pdf
Absolutnie najważniejszą spraw* w pomiarach wielkości doświadczalnych jest rzetelność wynik*w.
OSZACOWANIE NIEPEWNOŚCI POMIARU
Pomiar i zapis wyniku pomiaru
Aby cokolwiek zmierzyć, musimy znać definicję mierzonej wielkości (np. co to jest długość?)
oraz jej jednostkę (np. metr), musimy dysponować sprawnym przyrządem pomiarowym (np. liniałem czy taśmą metalowa, suwmiarka, śrubą mikrometryczna) wyskalowanym według wzorca. Porównując wielkość mierzoną (np. długość stołu) z jednostkową długością (np. 1 mm na przymiarze metalowym) - uzyskamy wynik pomiaru, to jest liczbę wraz z jednostka (np. 1522 mm).
Liczba otrzymana w wyniku procedury pomiarowej wraz z jednostką, np. przytoczony powyżej rezultat pomiaru długości stołu 1522 mm, nie jest pełną informacją o mierzonej wielkości. Potrzebna jest również ocena wiarygodności uzyskanego rezultatu polegająca na oszacowaniu tzw. niepewności wyniku. Najczęściej wykorzystuje się pojecie niepewności standardowej (u). Przyjęto umowę, że wynikiem pomiaru jest uzyskany liczbowy rezultat pomiaru wraz z wartością liczbową oszacowanej niepewności standardowej -obie liczby reprezentują pewne wielkości, wyrażone przy użyciu tej samej jednostki! Niepewność standardową zaokrągla się do maksymalnie dwóch cyfr znaczących, a wynik pomiaru zaokrągla się i podaje z miejscami znaczącymi zgodnymi co do pozycji z niepewnością. Na przykład, zapisujemy wynik: 1522 z niepewnością 1, ale nie 1522 z niepewnością 0,9. Albo 1,00061 (u = 0, 00027), czy zaokrąglony 1,0006 (u = 0, 0003), ale nie 1,0006 (u = 0, 00027). Karygodnym jest podawanie wszystkich cyfr wynikających z obliczeń numerycznych przy użyciu kalkulatora, np.: 1522,79346214 (u = 1, 35791622).
Rozróżniamy dwie metody obliczeń niepewności pomiaru:
metodę typu A (stosowana dla serii pomiarów) lub
metodę typu B (dla pojedynczego pomiaru) niepewność szacowana jest z niepewności wzorcowania przyrządu lub w oparciu o tzw. działkę elementarna stosowanego miernika).
Ocena niepewności typu B (pomiar jednokrotny)
Dość często w życiu codziennym, w technice i nauce uznajemy za wystarczające jednokrotne
wykonanie pomiaru. Do każdego przyrządu pomiarowego powinna być dostarczona informacja producenta o dokładności z jaką mierzy dany przyrząd (często sprowadza się ona do podania tzw. błędu maksymalnego - maksymalnej różnicy między wynikiem poprawnego odczytu ze skali przyrządu a wartością prawdziwą). W przypadku braku takiej informacji przyjmuje się, ze dokładność, z jaką mierzy dany przyrząd jest równa wartości działki elementarnej (np. 0,01 mm dla śruby mikrometrycznej, czy tez 1 mm dla przymiaru metrowego). Podobnie, wykorzystując przyrząd analogowy, np. woltomierz wychyłowy magnetoelektryczny, możemy oszacować dokładność wyniku pomiaru na podstawie tzw. klasy przyrządu. Klasa przyrządu to wielkość procentowa (podawana zwykle na skali przyrządu) przez którą trzeba pomnożyć używany zakres pomiarowy aby otrzymać dokładność pomiarową. I tak, pomiar napięcia 12,5 V przy zakresie 30 V, przyrządem klasy ”1”, wykonany jest z dokładnością wynoszącą 1% z 30 V = 0,3 V. Klasa przyrządu jest więc liczbą która określa jaki procent używanego w pomiarze zakresu przyrządu może być utożsamiany z dokładnością pomiarową.
Oznaczmy dokładność pomiaru przez Δ - jest to zwykle najmniejsza działka używanego przyrządu . Wtedy niepewność standardowa typu B, uB, pomiaru tym przyrządem wyraża się wzorem
![]()
Przykład 1.
Zmierzono suwmiarką grubość płyty stalowej i odczytano wynik 24,8 mm. Wartość działki elementarnej suwmiarki równa jest 0,1 mm. Zapiszemy wynik pomiaru: 24,8 mm (Δ= 0, 1mm) a niepewność standardowa wynosi uB , równa 0,06 mm.
Ocena niepewności typu A (pomiar wielokrotny)
Znacznie dokładniej można ocenić mierzoną wielkość wielokrotne powtarzając ten sam pomiar. Na przykład, wyniki pomiaru średnicy dość długiego, metalowego drutu o przekroju kołowym, wykonywane śrubą mikrometryczną w różnych miejscach drutu mogą znacząco się różnić. Oznaczmy kolejne wyniki n-krotnie powtórzonego pomiaru przez xi, gdzie indeks i oznacza numer pomiaru (i = 1, ..., n). Wówczas średnia arytmetyczna xsr z wyników pomiarów jest dobrym oszacowaniem wartości oczekiwanej μ:
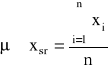
Miarą rozproszenia wyników w serii pomiarowej jest
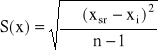
Wielkość S(x) jest oszacowaniem tzw. odchylenia standardowego pojedynczego pomiaru a więc miary rozproszenia mierzonej wielkości wokół jej wartości oczekiwanej.
Natomiast niepewność standardową typu A, uA, mierzonej wielkości x utożsamiamy w tym przypadku z odchyleniem standardowym średniej S(xsr); i tak niepewność standardowa uA opisana jest wzorem:
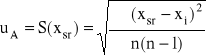
Przykład 2).
Zmierzono śrubą mikrometryczną średnicę drutu miedzianego. Wykonano 10 pomiarów średnicy d i uzyskano kolejno wyniki (w mm): 2,46; 2.49; 2.52; 2,47; 2,50; 2,51; 2,48; 2,49; 2,45; 2,50. Jaka jest średnica tego drutu i z jaką niepewnością została określona?
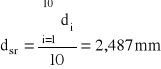
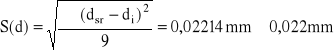
S(d) charakteryzuje rozrzut wyników wokół wartości średniej. Niepewność standardowa obliczona metodą typu A (uA(d)) wynosi
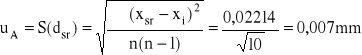
.
Ponieważ jednak poszczególne wartości różnią się znacząco miedzy sobą i różnice te sięgają 0,05
mm, to świadczy to o odstępstwie „modelu pomiarowego” naszego drutu (jednorodny cylinder, o stałej - wzdłuż całej długości- średnicy) od sytuacji rzeczywistej. Dlatego jako niepewność pomiaru lepiej jest wtedy stosować S(d).
Ostatecznie wynik pomiaru średnicy drutu możemy zapisać w postaci: d = 2,49 (0,02) mm.
JAK PRZEDSTAWIAĆ WYNIKI POMIARÓW NA WYKRESIE I JAK SZACOWAĆ NIEPEWNOŚCI WIELKOŚCI MIERZONYCH POŚREDNIO
Powiedzmy, że naszym celem jest pomiar prędkości dźwięku w CO2 a następnie obliczenie z prędkości dźwięku współczynnika κ=Cp/CV (który oczywiście na podstawie tej prędkości można obliczyć) .
Załóżmy też , że chcąc zmierzyć prędkość dźwięku w CO2 zmierzono długości fal dźwiękowych w zależności od częstości dźwięku, uzyskując wyniki (i niepewności tych wyników):
częstość f[Hz] |
1/f [s] |
λsr [m] |
δ(λ)[m] |
400 |
1/400 |
0.645 |
0.015 |
600 |
1/600 |
0.430 |
0.010 |
750 |
1/750 |
0.344 |
0.005 |
900 |
1/900 |
0.288 |
0.015 |
Prędkość dźwięku łączy się z długością fali relacją
|
(1) |
Z kolei, szukany współczynnik κ=Cp/CV oblicza się korzystając ze związku prędkości dźwięku z własnościami ośrodka sprężystego (czyli gazu)
|
(2) |
gdzie:
R-stała gazowa
μ-masa molowa gaz
Podstawowym sposobem wizualizacji wyników pomiarowych jest ich
Przedstawienie wynik*w λ(f) na wykresie
Można oczywiście wprost zrobi* wykres λ(f) (czyli tak jak poniżej), ale ze względu na relację λ=V/f wykres będzie hiperbol*, z której niewiele informacji da się w prosty sposób wyciągnąć.
. (rys 1). 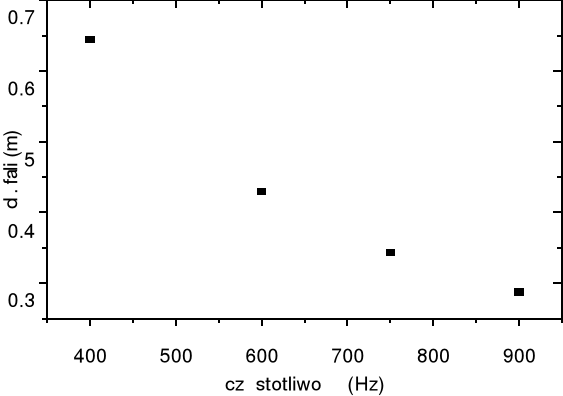
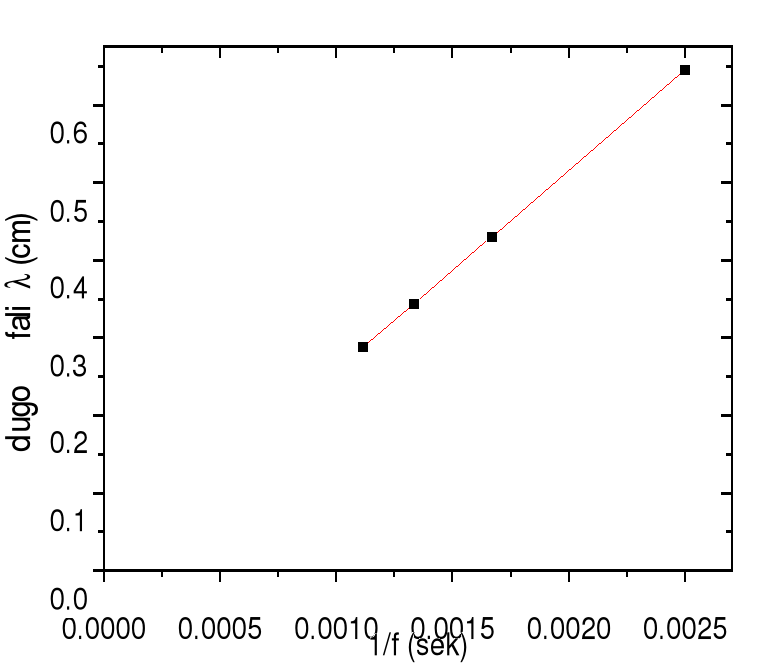
Dlatego bardziej celowe jest przedstawienie wynik*w na wykresie λ(1/f):
Ponieważ , więc λ w funkcji 1/f powinna dawać linię prostą o współczynniku kierunkowym równym V, tj. poszukiwanej wielkości.
|
(3) |
Zatem λ w funkcji (1/f) jest prostą o współczynniku kierunkowym V i wyrazie wolnym =0. Wykres w tym układzie osi przedstawiono na Rys 2, gdzie podano też dopasowane metodą najmniejszych kwadratów parametry prostej.
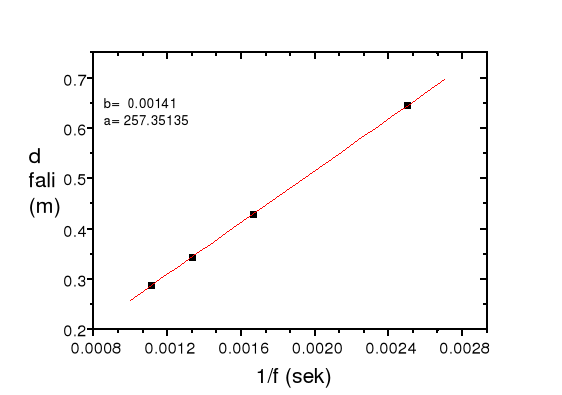
UWAGI:
1.Nale*y pamięta* o dobrze opisanych osiach wykresu (wymiary:[cm], [s]; jednostka). Proszę też zwrócić uwagę, że wykres nie musi zaczynać się od punktu (0.0):
|
|
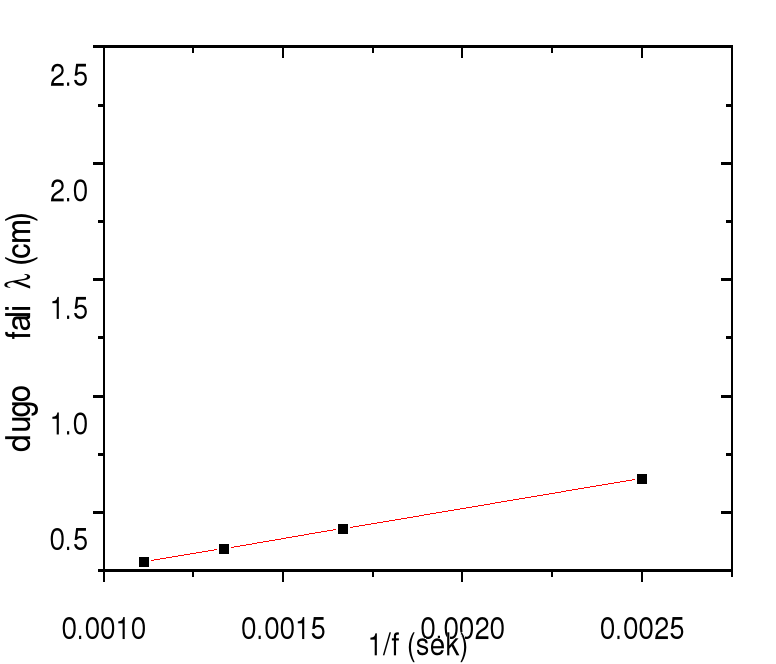
jak też musi wykorzystywać cała dostępną przestrzeń rysunku:
2.Obliczone poprzednio niepewności λ (f przyjmujemy jako warto** określoną bez błędu) muszą by* zaznaczone na wykresie. Czasem niepewność zawiera się w „grubo*ci” punktu (tak jak na rysunku powyżej), ale ten fakt musi by* zaznaczony w opisie.
3)Dopasowanie krzywej teoretycznej (tutaj: prostej) do wykresu wynik*w doświadczalnych.
Prostą λ=a*(1/f) +b dopasowuje się metod* najmniejszych kwadrat*w (tj. tak dobiera się prostą, aby suma odległości od niej do wszystkich punkt*w doświadczalnych by*a minimalna). Ta procedura znajduje się w większości kalkulator*w, w każdym razie takich, które szanujący się inżynier mieć powinien. Odpowiednie wzory na współczynniki dopasowania mają postać:
![]()
,
gdzie: 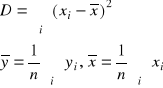
Wyniki tej procedury dla naszego przypadku pokazano na wykresie (rys. 2). Jako wniosek z obliczeń należy jednak wyra*nie napisać:
V=257.3±0.6 [m/s],
gdzie niepewność została obliczona na podstawie odchylenia standardowego parametrów dopasowania prostej (jeszcze raz przypominam: jeśli nawet kalkulator podał wartość np. 257.345678912, ale wiemy, że niepewność jest 0.6, to zostawienie wszystkich cyfr świadczy, że piszący niczego nie rozumie i będzie to traktowane jako błąd!!!). Wzory na takie parametry są albo dostępne w kalkulatorze (czyli stosując metodę najmniejszych kwadratów możemy je też odczytać), lub też trzeba z nich skorzystać "na piechotę”. Te wzory to:
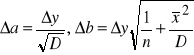
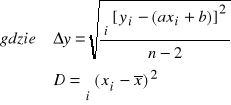
Można też skorzystać ze wzorów:
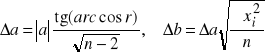
gdzie r jest współczynnikiem korelacji dostępnym we wszystkich kalkulatorach w których jest funkcja regresji liniowej, a n jest ilością pomiarów.
Teoretycznie, parametr b powinien być równy zeru i widać, *e w granicach niepewności pomiarowej tak rzeczywiście jest (chociaż jest to wynik aż podejrzanie dobry: zwykle dopasowanie do prostej jest znacznie gorsze i nie należy się tym specjalnie przejmować).
Dopasowaną prostą należy nanieść na wykres (czyli tak, jak na Rys. 2)
Obliczenie współczynnika κ i oszacowanie jego niepewności
Wiemy zatem, że prędkość dźwięku w gazie wynosi V=257.3±0.6 [m/s]. Naszym celem jest również obliczenie współczynnika κ na podstawie wzoru (2) (dostajemy z niego wyrażenie na wartość κ):
.
Używając danych tablicowych R i μ oraz wielkości zmierzonych (zmierzone jest nie tylko V, ale też temperatura otoczenia T) dostajemy: (μCO2=44g/mol, R=8.314J/molK, V=257m/s, T=295K)
κ=1.185
Jak teraz oszacować niepewność tej wielkości?
Robi się to stosując prawo przenoszenia niepewności. W ogólności, jeśli obliczana wartość Y (u nas κ) jest funkcją zmiennych x,y,z..., które mierzymy bezpośrednio (u nas te zmienne to V, oraz T), to wartość niepewności możemy oszacować wg. przepisu:
|
(to jest oczywiście pierwiastek z sumy kwadratów cząstkowych pochodnych pomnożonych przez kwadraty różniczek).Wartości różniczek dx, dy, itd. interpretujemy jako niepewności odpowiednich wartości x, y, itd. Czyli: dx=u(x), dy=u(y), itd. Zakładając, że κ jest funkcją 2 zmiennych T i V otrzymujemy:
|
(5) |
Szczególnie prostą postać dostanie się, jeśli obliczymy niepewność względną u(κ)/κ
|
(6) |
Uwzględniając niepewności prędkości i T (u(V)=0.6m/s i u(T)=1o) dostajemy u(κ)=0.02.
Zatem κ=1.19±0.02
2
Rys. 2
tak nie!!
tak nie!!
Wyszukiwarka
Podobne podstrony:
lepkość cieczy edwqed, Technologia chemiczna, Fizyka, semestr 2, Laborki, Sprawozdania
nr 31, Technologia chemiczna, Fizyka, semestr 2, Laborki, Sprawozdania
obliczenia, Technologia chemiczna, Fizyka, semestr 2, Laborki, Sprawozdania
WYKRESY-1, Technologia chemiczna, Fizyka, semestr 2, Laborki, Sprawozdania
lepkość cieczy, Technologia chemiczna, Fizyka, semestr 2, Laborki, Sprawozdania
psfiz37, Technologia chemiczna, Fizyka, semestr 2, Laborki, Sprawozdania
dwadzescia, Technologia chemiczna, Fizyka, semestr 2, Laborki, Sprawozdania
ONP, Technologia chemiczna, Fizyka, semestr 2, Laborki, Sprawozdania
FIZ4a, Technologia chemiczna, Fizyka, semestr 2, Laborki, Sprawozdania
lepkość cieczy edwqed, Technologia chemiczna, Fizyka, semestr 2, Laborki, Sprawozdania
nr 31, Technologia chemiczna, Fizyka, semestr 2, Laborki, Sprawozdania
Opracowanie wyników pomiarów dla ćwiczenia lepkość, Fizyka laborka 13 lepkość
więcej podobnych podstron