IMIĘ I NAZWISKO Mariusz Kijak	Ćwiczenie C - 4 WYZNACZANIE WARTOŚCI DLA POWIETRZA METODĄ CLEMENSA - DESOMESA
ROK I KIERUNEK Fizyka Medyczna rok I
		OCENA	OCENA	OCENA
PROWADZĄCY prof. Krzesińska	DATA PODPIS	DATA PODPIS	DATA PODPIS

1. Cel Ćwiczenia

Wyznaczenie wartości κ dla powietrza metodą Clemensa - Desormesa

2. Część Teoretyczna

W ćwiczeniu, które przeprowadziłem należało wyznaczyć stosunek ciepła właściwego przy stałym ciśnieniu do ciepła właściwego przy stałej objętości. Zależność ta jest w skrócie nazywana grecką literą kappa - κ. Pomiar ten przeprowadzałem przez poddanie gazu o ciśnieniu p = ciśnieniu atmosferycznemu o temperaturze t = temp. otoczenia, który znajdował się w naczyniu zamkniętym trzem kolejnym przemianom:

Pierwsza przemiana - izotermiczna - zmieniam ciśnienie p gazu na ciśnienie p + h, za pomocą pompki, pozostawiając stałą temperaturę t. Objętość jest równa V.

Przemiana izotermiczna - przemiana termodynamiczna zachodząca przy stałej temperaturze ( T = const).

Prawo Boyle'a - Mariotte'a - prawo przemiany izotermicznej dla gazu doskonałego:

W izotermicznej przemianie stałej masy gazu iloczyn jego ciśnienia p i objętości V jest stały:

Mogę też powiedzieć, że ciśnienie gazu jest odwrotnie proporcjonalne do jego objętości. Wykres tej zależności nazywa się izotermą (jest nią w układzie (p,V) hiperbola):

Kolejna przemiana - adiabatyczna - otwieram kurek i przez około 2 sekundy naczynie jest połączone z atmosferą. Gaz rozprężając się do ciśnienia p wykonuje pracę, a jego temperatura t zmienia się o ∆t. Następuje również zmiana objętości z V do objętości V'

Przemiana adiabatyczna - przemiana termodynamiczna, która przebiega bez przepływu ciepła (Q = 0) i materii (m = const) między układem a otoczeniem.

Równanie przemiany adiabatycznej (Równanie Poissona):

Równanie opisujące zależność między objętością V gazu doskonałego, a jego ciśnieniem p w przemianie adiabatycznej:

κ - jest stosunkiem ciepła właściewego gazu pod stałym ciśnieniem c_p do ciepła właściwego gazu przy stałej objętości c_v :

Kappa dla gazów wynosi:

• dla gazów jednoatomowych c = 5/3

• dla gazów dwuatomowych κ = 7/5

• dla gazów wieloatomowych κ = 4/3.

Wykresem przemiany adiabatycznej w układzie (p,V) jest adiabata:

Trzecia przemiana - izochoryczna - po zamknięciu kurka gaz, objętość gazu pozostaje stała V' = const. Temperatura gazu zmienia się do temperatury otoczenia, która jest wyższa nią temp. gazu. Natomiast ciśnienie wzrasta do p + h'

Przemiana izochoryczna - przemiana termodynamiczna zachodząca przy stałej objętości (V = cosnt).

Prawo Charles'a - prawo przemiany izochorycznej gazu doskonałego:

W izochorycznej przemianie stałej masy gazu ciśnienie jest wprost proporcjonalne do jego temperatury bezwzględnej:

p - ciśnienie stałej masy gazu w temperaturze t wyrażonej w skali Celsjusza

p₀ - ciśnienie tego gazu w 0˚C

β = (273,15˚C)^-1 - współczynnik termicznej prężności gazu,

Wykres tej zależności nazywa się izochorą (jest nią w układzie (p,T) linia prosta przechodząca przez początek układu):

Trzy kolejne stany gazowe charakteryzuję następujące wielkości:

I stan:

p + h - ciśnienie

V - objętość

t - temperatura

II stan:

p - ciśnienie

V' - objętość

t - ∆t - temperatura

III stan:

p + h' - ciśnienie

V' - objętość

t - temperatura

Ponieważ gaz posiada tę samą temperaturę w stanie pierwszym jak i w trzecim, związek pomiędzy początkową i końcową objętością oraz ciśnieniem można wyrazić za pomocą prawa Boyle'a i Mariotte'a

Przemiana adiabatyczna przebiega zgodnie z prawem Poissona

Wzór pierwszy zapisuję w następującej postaci:

Drugi w postaci:

Po wykonaniu podstawień otrzymuję:

Po logarytmowaniu i wykonaniu prostych obliczeń otrzymuję:

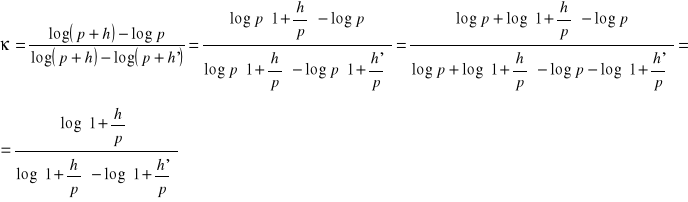
Na podstawie definicji, że dla małych wartości x log(1+x) = x mogę zapisać w moim przypadku, że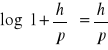
oraz

Otrzymuję:

3. Przyrządy pomiarowe

• Naczynie zamknięte (butla) połączone z pompką przy pomocy kurka

• Manometr cieczowy

4. Przebieg ćwiczenia

• Ustawiam kurek w takim położeniu aby butla była połączona z pompką i wypompowuje pewną ilość powietrza, a następnie zamykam kran.

• Odczekuje chwilę, aby temperatura gazu zrównała się z temperaturą otoczenia, a następnie odczytuje różnicę poziomów h cieczy w manometrze

• Na krótką chwilę ustawiam kurek w takim położeniu aby butla połączona była z atmosferą. Gdy ciśnienie spadnie do wartości ciśnienia atmosferycznego, zamykam kran i odczekuję chwilę, aż powietrze podgrzeje się do temperatury otoczenia, a następnie odczytuję wskazanie manometru h'

• Powtarzam pomiary z punktów 1 - 3 dziesięć razy.

• Wyniki pomiarów przedstawiam w tabelce

• Dla każdego pomiaru obliczam κ

• Obliczam średnią wartość κ i odchylenie standardowe średniej arytmetycznej

• Obliczam niepewność ∆κ zakładając poziom ufności ά = 0.95 według rozkładu Studenta - Fishera

5. Wyniki pomiarów

L.p.	Zmiana ciśnienia h [cm]	Zmiana ciśnienia h' [cm]	Stosunek Cp do Cv κ
1	10.3	2.9	1.39
2	10.5	3.4	1.48
3	9.2	2.5	1.34
4	9	2.7	1.43
5	9	2.6	1.41
6	9	2.7	1.39
7	7	1.6	1.30
8	7	1.5	1.27
9	9.3	3.1	1.39
10	9.9	3.1	1.45

6. Obliczenia

Obliczyłem κ dla każdego pomiaru ze wzoru

1. 
   

2. 
   

3. 
   

4. 
   

5. 
   

6. 
   

7. 
   

8. 
   

9. 
   

10. 
    

Obliczam średnią wartość κ ze wzoru

Obliczam odchylenie standardowe metodą Studenta Fishera dla założonego poziomu ufności ά = 0.95

Współczynnik Studenta Fishera dla założonego poziomu ufności ά = 0.95 i dziesięciu pomiarów n = 10 wynosi t_ά = 2.3

Wykonuje obliczenia

Wartość κ jest równa:

7. Wnioski

• Tablicowa wartość κ wynosi 1.40.

• Wynik, który otrzymałem jest bliski wartości tablicowej.

• κ jest wielkością niemianowaną.

• Sądzę, że doświadczenie zostało wykonane w sposób prawidłowy i że otrzymane wyniki są zadowalające.

---