CZĘŚĆ TEORETYCZNA

Metody wyznaczania rozkładów naprężeń i odkształceń dotyczy przekrojów brył i obszarów dostatecznie odległych od miejsc przyłożenia w postaci sił skupionych, jak również dostatecznie odległych od miejsc nagłych zmian kształtu brył. Były więc analizowane przypadki, dla których obowiązywał niezaburzony rozkład naprężeń zgodnie z zasadą de Saint-Venanta. Wszelkie zmiany przekroju pręta powodują lokalny wzrost naprężeń, tym gwałtowniejszy, im bardziej raptowna jest zmiana jego wymiarów poprzecznych. Takie obliczenia teoretyczne w przekroju 1-1 za pomocą wzoru,

σ₀ = P / F

takie fragmenty ciał, jak skoki przekroju, otwory są nazwane karbami. Maksymalne naprężenia spowodowane istnieniem karbu są kilkakrotnie większe niż tzw. naprężenia nominalne.

Rozpatrując tarczę o danej szerokości, grubości, z otworem o danej średnicy. Pod działaniem siły P występują naprężenia nominalne równe

σ_0­ = P / ( b * δ ) .

Jest to jednowymiarowy stan naprężeń. Analogicznie można policzyć naprężenia w przekroju osłabionym otworem.

σ'_0­ = P / ( δ * ( b - d ) ).

Zatem widać, że σ'₀>σ₀.

Takie podejście nie uwzględnia istnienia karbu. Stan naprężeń powinien być dwuwymiarowy, powodem jest tego fakt, że włókna tarczy przecięte otworem nie mogą przenosić sił wzdłużnych tuż przy granicy otworu i siły te są przejmowane przez najbliższe włókna nie przecięte otworem. Dla różnych przekrojów rozkład naprężeń jest różny, zatem należy rozpatrywać każdy z przypadków oddzielnie. W punktach bardzo blisko położonych otworu naprężenia są bardzo podwyższone. Taki lokalny wzrost wartości naprężeń nazywamy spiętrzeniem lub koncentracją naprężeń. Zjawisko spiętrzenia naprężeń występuje w wielu sytuacjach praktycznych, tam gdzie mamy do czynienie z karbem. W obliczenia stosuje się współczynnik spiętrzenia naprężeń, który można zdefiniować:

α_k = (σ_x)max / σ₀ lub α'_k = (σ_x)max / σ'_{0 .}

Wartość nominalną naprężeń można obliczyć w konkretnym przypadku. Współczynnik spiętrzenia naprężeń może być zdefiniowany na różne sposoby.

Rozważając inne tarcze, taką jak badana na zajęciach. Najbardziej osłabiony punkt może być przesunięty względem pełnego przekroju. Przecinając tarczę to wysiłek stanowić będzie siła P oraz moment gnący. Naprężenia nominalne będą superpozycją naprężeń spowodowanych rozciąganiem σ_r oraz naprężeń spowodowanych zginaniem σ_g. Należy zauważyć, iż w zależności mimośrodu e mogą pojawić się naprężenia ściskające mniejsze od zera. Będzie nas interesował również współczynnik spiętrzeń α'_k = σ_k / σ'_0k. Wartość σ_k wyznaczamy na podstawie pomiarów tensometru w pobliżu punktu K. Na wartość współczynnik spiętrzenia mają wpływ wymiary tarczy, takie jak promień wycięcia, szerokość tarczy oraz głębokość wycięcia. Spiętrzenie naprężeń jest szczególnie groźne przy obciążeniach dynamicznych i o długotrwałym działaniu - obniża się wytrzymałość materiałów, zwana zmęczeniem materiału. Zmęczenia materiału jest własnością nieprawidłową i powinna być nieosiągalna.

PRZEBIEG ĆWICZENIA

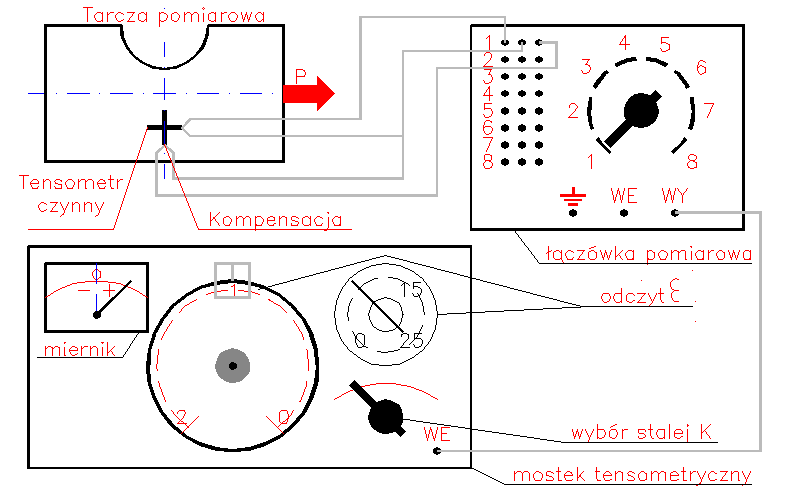
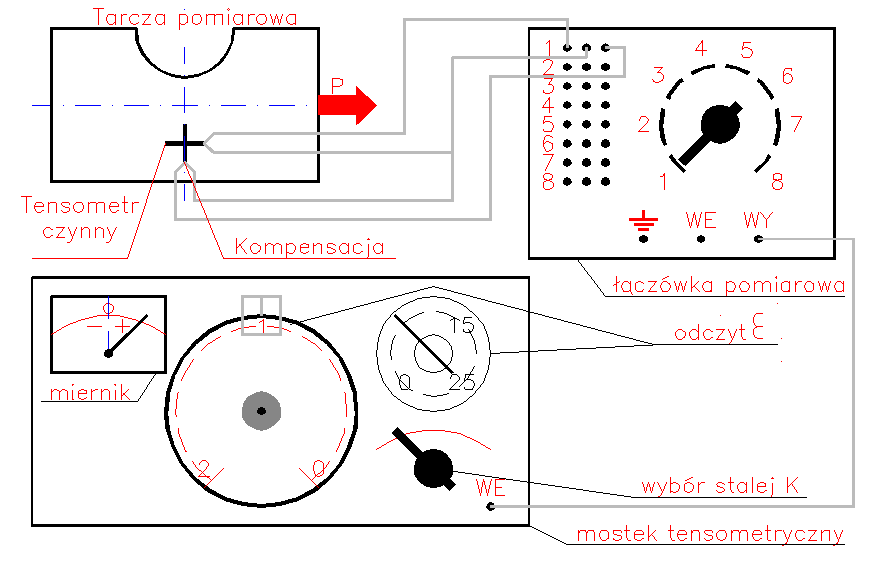
Pierwszą rzeczą jako zrobiliśmy to było zapoznanie się z ustawieniem aparatów pomiarowych, które były ustawione według schematu który jest pokazany na rys1. Później przystąpiliśmy do odczytów wielkości ε dla zadanej próbki. Wyniki te są zamieszczone w tablicy 1. Pomiary są przeprowadzone dwukrotnie i wyciągnięta została średnia arytmetyczna. Oto tabela wyników:

Kanał	0KG	40KG	80KG	120KG
1	14.15	14.22	14.27	14.32
2	14.85	14.88	14.9	14.94
3	13.8	13.82	13.84	13.85
4	13.82	13.83	13.84	13.85
5	14.05	14.06	14.06	14.07
6	13.94	13.94	13.94	13.95

Schemat ustawienia stanowiska pracy

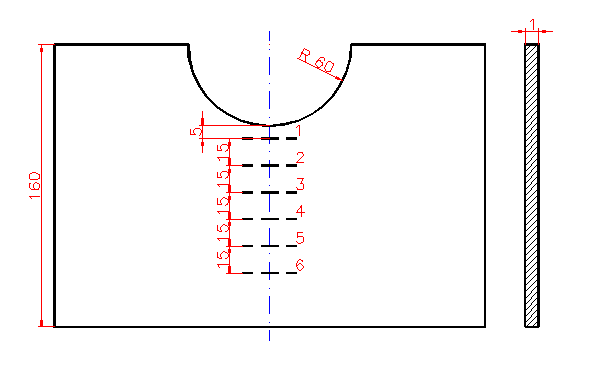
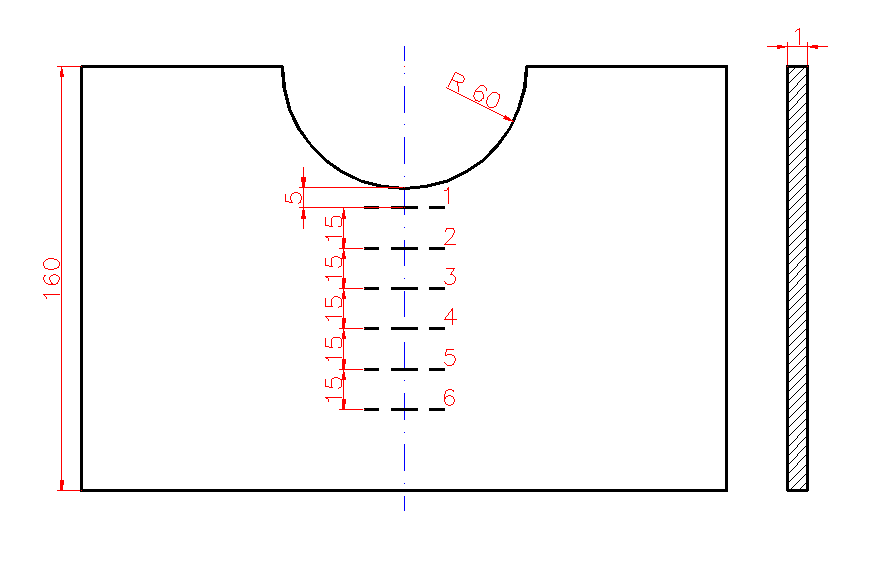
Schemat tarczy pomiarowej

Kolejną czynnością wykonaną było obliczenie σ₀, σ'_0. I tak dla zadanej siły np. 65 KG naprężenia nominalne wynoszą:

σ₀ = 65 / 0,16 / 0,001 = 406 250 Pa,

zaś σ'₀ = 65 / 0,13 / 0,001 = 500 000 Pa.

Kolejną czynnością było obliczenie ε_xi dla kilku obciążeń tarczy, dla danych wartości ε dokonaliśmy obliczenia naprężeń σ_xi = E ( ε_xi - ε_oi ), wyniki te zamieściliśmy w tabeli 2.

B=160 δ=1 d=60 r=30						k=2,15 E=2,1*10^11 Pa
Kanał		ε0i (P=0)	P=65[KG]				P=110[KG]
						ε xi ^O/oo	ε xi - ε 0i ^O/oo	σ xi [MPa]			ε xi ^O/oo	ε xi - ε 0i ^O/oo	σ xi [MPa]
1	14,17		14,26	0,09	18,9Mpa		14,27	0,1	21
2	14,85		14,93	0,08	16,8		14,93	0,08	17
3	13,81		13,84	0,03	6,3		13,85	0,04	8,4
4	13,82		13,83	-0,01	-2,1		13,84	0,02	4,2
5	14,15		14,06	-0,09	-18,9		14,565	0,41	86,1
6	13,94		13,94	0,0	0		13,935	-0,005	-1,05

Kolejną czynnością jaką powinniśmy wykonać to porównanie naprężeń nominalnych z otrzymanymi podczas ćwiczenia. Zatem naprężenia nominalne dla obciążenia P=65KG wynoszą kolejno dla kanałów:\

σ'₀ = σ_r + σ_g = P / ( g * (b - r)) + -12Pe / (g * ( b - r )³) * y

Dla P= 65 [kG]

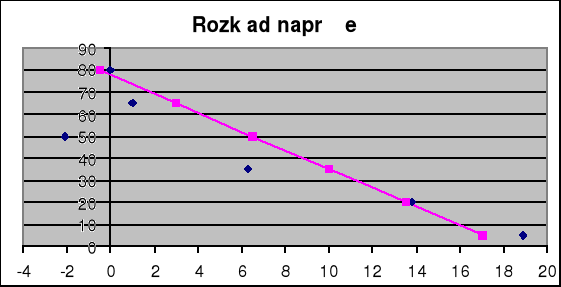
y= 30 [mm], σ₀^'=650/[1(160-60)]+[-12*650*(30)*30]/[1*(160-60)³]=6,5-7,02= -0,55 [MPa]

y= 15 [mm], σ₀^'=650/[1(160-60)]+[-12*650*(30)*15]/[1*(160-60)³]=6,5-3,51= 2,99 [MPa]

y= 0 [mm], σ₀^'=650/[1(160-60)]+[-12*650*(30)*0]/[1*(160-60)³]=6,5+0=6,5 [MPa]

y= -15 [mm], σ₀^'=650/(160-60)+[-12*650*(30)*(-15)]/(160-60)³= 6,5+3,51=10,01[MPa]

y= -30 [mm], σ₀^'=650/(160-60)+[-12*650*(30)*(-30)]/(160-60)³=6,5+7,02=13,52 [MPa]

y= -45 [mm], σ₀^'=650/(160-60)+[-12*650*(30)*(-45)]/(160-60)³= 6,5+10,53=17,03 [MPa]

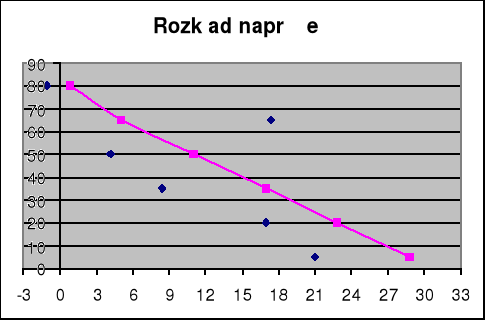
Dla P= 110 [kG]

y= 30 [mm], σ₀^'=1100/(160-60)+[-12*1100*(30)*30]/(160-60)³=11-11,88=-0,88 [MPa]

y= 15 [mm] σ₀^'=1100/[1(160-60)]+[-12*1100*(30)*15]/[1*(160-60)³]=11-5,94=5,06 [Mpa]

y= 0 [mm] σ₀^'=1100/[1(160-60)]+[-12*1100*(30)*0]/[1*(160-60)³]=11 [Mpa]

y= -15 [mm], σ₀^'=1100/(160-60)+[-12*1100*(30)*(-15)]/(160-60)³= 11+5,94=16,94 [MPa]

y= -30 [mm], σ₀^'=1100/(160-60)+[-12*1100*(30)*(-30)]/(160-60)³=11+11,88=22,88 [MPa]

y= -45 [mm], σ₀^'=1100/(160-60)+[-12*1100*(30)*(-45)]/(160-60)³=11+17,82=28,82 [MPa]

Wykres naprężeń nominalnych i otrzymanych w wyniku pomiarów dla 65 KG

Wykres naprężeń nominalnych i otrzymanych w wyniku pomiarów dla 110 KG

Obliczenie współczynnika koncentracji naprężeń

Współczynnik koncentracji naprężeń policzymy dla dwóch obciążeń: 65 [kG] i 110 [kG] w okolicach granicy karbu, gdzie naprężenia są największe. Otrzymujemy go ze wzoru:

σ_XMAX- maksymalne naprężenia otrzymane doświadczalnie;

σ₀'-naprężenia wyliczone w sposób nie uwzględniający wpływu karbu

α_K' = σ_{XMAX /}σ₀'

Dla obciążenia 65 [kG]

α_K' = 18,9/6,5= 2,9

Dla obciążenia 110 [kG]

α_K' = 21/11= 1,909

Wnioski:

• Przeprowadzone doświadczenie wykazało, iż naprężenia w przekroju osłabionym karbem w bezpośredniej bliskości tego karbu są znacznie większe od naprężeń uzyskanych na drodze obliczeń analitycznych;

• Naprężenia policzone bez uwzględnienia karbu mogą być nawet kilkakrotnie mniejsze od rzeczywistych naprężeń ekstremalnych.

• Współczynnik koncentracji naprężeń maleje wraz ze wzrostem obciążenia, co oznacza, iż przy dużych obciążeniach błąd w przypadku nieuwzględnienia karbu jest mniejszy niż w przypadku niewielkich obciążeń.

• W przypadku karbu nie można w obliczeniach pomijać jego wpływu, gdyż powoduje on, iż naprężenia rzeczywiste są kilkakrotnie większe od naprężeń obliczeniowych, co może prowadzić do błędnych wniosków wytrzymałościowych.

• W zależności od przyjętego modelu w dalszej odległości od miejsca karbu naprężenia obliczeniowe są bądź większe, bądź mniejsze od rzeczywistych co przemawia za tym aby w przypadku konstrukcji odpowiedzialnych wykonywać doświadczalne próby wytrzymałościowe.

• W wyniku pomiarów okazało się również, iż w niektórych punktach przekroju osłabionego niesymetrycznie nie występują naprężenia rozciągające, lecz naprężenia ściskające. Częściowo potwierdza to prawdziwość wzorów teoretycznych, które zakładają taką możliwość.

---