I. Wiadomości podstawowe.

Zderzenia sprężyste i niesprężyste.

Cząstki naładowane przechodząc przez materię doznają zderzeń z atomami tj. elektronami i jądrami atomów, w rezultacie czego zostają rozproszone (tzn. zachodzi zmiana kierunku ich ruchu) i tracą część swojej energii kinetycznej.

Rozróżniamy zderzenia :

a) sprężyste,

b) niesprężyste.

W zderzeniach sprężystych obowiązuje zasada zachowania pędu i zasada zachowania energii kinetycznej zderzających się cząstek. W zderzeniach niesprężystych część energii kinetycznej zderzających się cząstek przechodzi w inne rodzaje energii.

Zderzenia niesprężyste dzielimy na:

a) zderzenia niesprężyste z zewnętrznymi elektronami atomów, powodujące jonizację atomów (tzw. hamowanie jonizacyjne),

b) zderzenia niesprężyste z jądrami połączone z wypromieniowaniem energii (tzw. promieniowanie hamowania).

Zderzenia niesprężyste związane z przekazywaniem energii zderzającej się cząstki na jonizację atomów zachodzą wtedy, gdy cząstka przechodzi stosunkowo daleko od jądra i zderza się z zewnętrznymi elektronami atomów, które wskutek uzyskanej energii odrywają się od atomu. Powstaje wówczas para jonów (jon dodatni i elektron). Jeżeli cząstka przechodzi blisko jądra i nie następuje jej wychwyt przez jądro, wówczas zostaje ona rozproszona z ewentualną równoczesną emisją kwantu promieniowania.

Powstawanie promieniowania rentgenowskiego.

Promienie Rentgena powstają zawsze tam, gdzie wiązka promieni katodowych uderza
w pewną substancję i zostaje zahamowana. Do ich wytworzenia stosuje się lampy rentgenowskie, w których zogniskowana wiązka promieni katodowych, tzn. elektronów swobodnych o dużej energii, uderza w metalową anodę (antykatodę). Rozróżnia się dwa typy lamp rentgenowskich:

a) lampy jonowe z zimną katodą,

b) lampy Coolidge'a z żarzoną katodą.

Komory jonizacyjne.

Rozróżniamy dwa typy komór jonizacyjnych:

a) komory prądowe,

b) komory impulsowe.

Jonizacyjne komory prądowe służą do pomiaru całkowitej jonizacji, wywołanej wewnątrz komory przez promieniowanie o stosunkowo dużym natężeniu. W przypadku małego napięcia przyłożonego do elektrod komory w gazie zachodzi zjawisko rekombinacji jonów, które maleje wraz ze wzrostem napięcia. Prąd jonizacji rośnie z napięciem i przy pewnym napięciu uzyskuje się nasycenie prądu jonizacji. Jeżeli promieniowanie wydziela w jednostce czasu w objętości komory jonizacyjnej energię E, to natężenie prądu jaki płynie wewnątrz komory, wynosi

gdzie: e - ładunek elementarny, ε - energia stracona na wytworzenie jednej pary jonów.

Impulsowa komora jonizacyjna służy do pomiaru jonizacji wywołanej przez pojedynczą cząstkę lub grupę cząstek przelatujących równocześnie przez komorę. Amplituda impulsu jest proporcjonalna do jonizacji wytworzonej przez cząstkę i dla danej komory zależy od jej pojemności.

Licznik Geigera-Mullera.

L

W

W stanie normalnym gaz wypełniający licznik nie przewodzi prądu elektrycznego. Jeżeli jednak do wnętrz licznika dostanie się cząstka naładowana , jonizująca gaz wówczas oderwanie od atomów gazu elektrony przyciągane przez dodatnio naelektryzowaniu drut uzyskuje w silnym polu elektrostatycznym panującym wokół anody tak duże prędkości , że przy zderzeniach
z obojętnymi atomami gazu jonizują je. Powstałe elektrony z kolei rozpędzają się i wywołują dalsza jonizację. W bardzo krótkim czasie powstaje lawina elektronów , która przenosi stosunkowo duży ładunek. Przez licznik , a więc w całym obwodzie przepływa prąd elektryczny wywołujący krótkotrwały impuls . Wywołanie lawinowe daje zwiększenie liczby elektronów zbieranych przez anodę wywołując impuls w liczniku. Za pomocą licznika można również rejestrować fotony , które wybijają ze ścianek licznika lub z atomów gazu wypełniającego licznik.

Liniowy i masowy współczynnik pochłaniania.

Przy przejściu promieni X lub γ przez materiał zachodzi charakterystyczna dla promieniowania elektromagnetycznego absorpcja wykładnicza, w odróżnieniu od absorpcji cząstek naładowanych, dla których istnieje określony związek między energią i zasięgiem. Dla danej długości fali zależność natężenia wiązki przepuszczonej przez absorbent od grubości
x absorbenta ma postać:

gdzie I jest natężeniem wiązki, która przeszła absorbent o grubości x, Io natężeniem wiązki padającej na absorbent, μ stałą dla danej długości fali, zwaną liniowym całkowitym współczynnikiem atenuacji absorbenta. Przez zróżniczkowanie powyższego związku otrzymujemy:

Współczynnik atenuacji określa względne osłabienie wiązki w warstwie o grubości jednostkowej. Wymiar współczynnika atenuacji wynosi 1/cm. Czasem używa się wielkości:

którą nazywamy masowym współczynnikiem atenuacji. Jego wymiar to cm²/g.

II. Schemat blokowy aparatury pomiarowej.

II

III I

gdzie:

I - licznik Geigera Mullera

II - zasilacz wysokiego napięcia ZWN - 42

III - przelicznik PT - 72

III. Tabele wyników.

Folia nr	Ilość impulsów m [imp]	Ilość impulsów / s z=m/t [imp/s]
Bez folii	6760	33,8
1	6485	32,4
2	5217	26,08
3	5492	27,46
4	5373	26,86
5	5241	26,2
6	5154	25,77
7	4667	23,33
8	4554	22,77
9	4283	21,41
10	4344	21,72
X	5609	28,04

n	G	m	S	d0=m/S
		[mG]	[g]	[cm^2]	[g/ cm^2]
1	11,2	0,0112	4	0,0028
2	11	0,011	4	0,00275
3	11,3	0,0113	4	0,00282
4	11,1	0,0111	4	0,00277
5	10,9	0,0109	4	0,00272
6	11,2	0,0112	4	0,0028
7	11	0,011	4	0,00275
8	11,4	0,0114	4	0,00285
9	11	0,011	4	0,00275
10	11,3	0,0113	4	0,00282
		mśr=0,01114	d0śr=0,002783

IV. Obliczenia.

n	k	z	lnz	k^2	k*lnz
1	0	32,4	3,520	0	0
2	1	26,08	3,261	1	3,261
3	2	27,46	3,312	4	6,624
4	3	26,86	3,290	9	9,87
5	4	26,2	3,265	16	13,06
6	5	25,77	3,249	25	16,245
7	6	23,33	3,149	36	18,894
8	7	22,77	3,125	49	21,875
9	8	21,41	3,063	64	24,504
10	9	21,72	3,078	81	27,702
X	10	28,04	3,333	100	33,33
	Σki=45		Σlnz=35,645	Σk^2=285	Σk*lnz=175,365

[imp/s]

ln z = 3,520

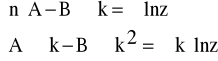
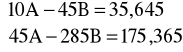
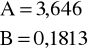
k	y(k) = A - B*k
0	3,646
1	3,4647
2	3,2835
3	3,1021
4	2,9208
5	2,7395
6	2,5582
7	2,3769
8	2,1956
9	2,0143
10	1,833

Obliczamy masowy współczynnik pochłaniania dla glinu

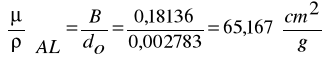
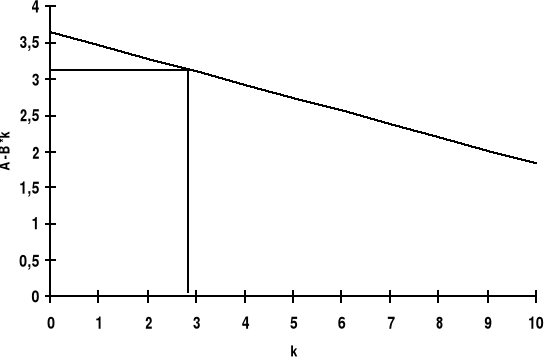
Z wykresu y(k) = ln z odczytujemy wartość k dla folii X k = 2,8

Grubość nieznanej folii obliczamy ze wzoru:

gdzie ρ = 2,67 [g/cm³]

V. Wnioski.

Przeprowadzone pomiary pozwoliły nam na wyznaczenie grubości folii aluminiowej Cała istota ćwiczenia opierała się na wykorzystaniu promieni β przechodzących przez kolejne próbki folii. Należy zwrócić uwagę na to, że natężenie promieni β przechodzących przez warstwy folii ulega osłabieniu na skutek pochłaniania i rozpraszania promieniowania. Masowy współczynnik pochłaniania dla glinu wyniósł 65,107 cm²/g.

Zmniejszenie natężenia promieniowania jest proporcjonalne do grubości folii. Pozwoliło nam to na wyznaczenie wartości k dla nieznanej folii k=0,8 a następnie na wyznaczenie grubości tej folii X=0,00291 cm.

---