CAŁKI KRZYWOLINIOWE
Niech K - krzywa w R3,
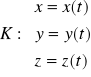
, gdzie ![]()
oraz ![]()
.
Zatem dowolny punkt (x,y,z) krzywej K można przedstawić w postaci
![]()
i krzywa K zadana jest przez wektor parametryzacji ![]()
K: ![]()
.
Definicja
Jeśli krzywa nie ma punktów wielokrotnych, tzn. gdy spełniony jest warunek ![]()
, to nazywamy ją łukiem zwykłym. Łuk zwykły jest łukiem skierowanym, gdy określony jest zwrot tego łuku, tzn. uporządkowanie punktów łuku odpowiadające wzrostowi parametru.
Zmiana parametru na przeciwny daje łuk przeciwnie skierowany -K:
Podstawiamy ![]()
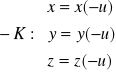
, gdzie ![]()
Definicja
Jeśli jedynym punktem wielokrotnym krzywej jest punkt początkowy i końcowy, tzn. jeśli w łuku zwykłym dopuścimy ![]()
, to krzywą nazywamy krzywą zamkniętą zwykłą.
Definicja
Krzywa zwykła zamknięta, zawarta w R2 dzieli płaszczyznę na dwa obszary: wnętrze, tzn. obszar ograniczony krzywą i zewnętrze (obszar na zewnątrz krzywej).
Jeśli w czasie obiegu po krzywej zamkniętej wnętrze znajduje się po stronie lewej, to krzywą nazywamy zorientowaną dodatnio i oznaczamy ![]()
.
Jeśli w czasie obiegu po krzywej zamkniętej wnętrze znajduje się po stronie prawej, to krzywą nazywamy zorientowaną ujemnie i oznaczamy ![]()
.
Definicja
Punkt ![]()
krzywej K, gdzie ![]()
nazywamy punktem osobliwym krzywej K, gdy zerują się pochodne ![]()
dla dowolnej parametryzacji tej krzywej.
Definicja
K - jest krzywą gładką![]()
![]()
![]()
)
![]()
K nie ma punktów wielokrotnych
![]()
K nie ma punktów osobliwych, tzn. ![]()
, ![]()
Każda krzywa, którą można podzielić na skończoną liczbę krzywych gładkich jest nazywana krzywą odcinkami gładką lub krzywą regularną.
Uwaga
Krzywa regularna jest prostowalna.
Całka krzywoliniowa nieskierowana
(całka krzywoliniowa funkcji skalarnej)
Niech
K - krzywa regularna w R3
f - pole skalarne, tzn ![]()
![]()
Wtedy
krzywą K dzielimy na n części o długościach
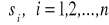
w każdej z krzywych cząstkowych wybieramy po jednym punkcie
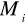
tworzymy sumę
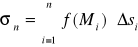
Definicja
Jeśli przy ![]()
i ![]()
istnieje granica ![]()
niezależna od sposobu podziału krzywej i od wyboru punktu Mi, to granicę tę nazywamy całką krzywoliniową nieskierowaną i oznaczamy![]()
.
Uwaga
Gdy zmienimy zwrot krzywej na przeciwny przy tym samym podziale krzywej i tych samych wybranych punktach, to nie zmienią się sumy ![]()
, a zatem nie zmieni się całka krzywoliniowa nieskierowana
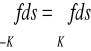
.
Twierdzenie (o zamianie całki krzywoliniowej nieskierowanej na całkę oznaczoną)
Jeżeli K - krzywa regularna,
![]()
to
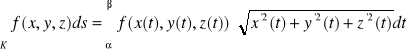
.
Przykład
Obliczyć całkę 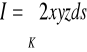
, gdzie K: 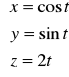
dla ![]()
.
Oczywiście krzywa K jest regularna oraz ![]()
. Zatem można zastosować twierdzenie o
zamianie całki krzywoliniowej na całkę oznaczoną.
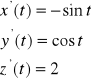
Stąd
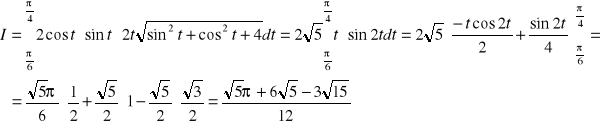
Uwaga
1. Jeśli krzywa K leży w płaszczyźnie OXY, ![]()
,
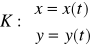
, gdzie ![]()
oraz
![]()
,
to
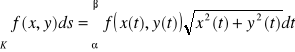
.
2. Jeśli krzywa K leż w płaszczyźnie OXY i zadana jest w sposób jawny, tzn.
![]()
to K możemy sparametryzować:
K: 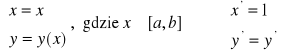
i wtedy
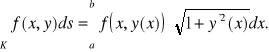
Przykład
Obliczyć 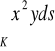
, gdzie![]()
, ![]()
.
Funkcja ![]()
dla ![]()
określa krzywą K.
Obliczamy ![]()
i korzystamy z uwagi 2.
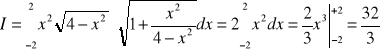
Interpretacja geometryczna całki krzywoliniowej niekierowanej
Niech

na K.
Wtedy
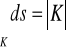
- długość krzywej K.
Niech K - krzywa płaska,
![]()
Wtedy
- pole części powierzchni walcowej znajdujące się pod wykresem funkcji f.
Interpretacja fizyczna całki krzywoliniowej nieskierowanej
Jeśli ρ - gęstość liniowa masy rozmieszczonej wzdłuż krzywej K, to
![]()
- masa krzywej K
Jeśli d - funkcja określającą odległość punktu krzywej K od pewnej prostej, to
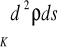
- moment bezwładności krzywej K względem tej prostej.
Uwaga
Niech ![]()
, gdzie ![]()
krzywa regularna dla i=1,…,n.
Wtedy definiujemy
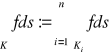
.
Całka krzywoliniowa skierowana
(całka krzywoliniowa funkcji wektorowej)
Niech K - krzywa regularna o początku A i końcu B, zawarta w ![]()
W - pole wektorowe, ![]()
![]()
![]()
Wtedy
dzielimy krzywą K na n krzywych punktami:
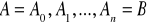
, gdzie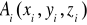
dla i=1,2,…,ntworzymy wektory cięciw:
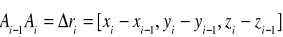
dla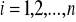
wybieramy po jednym punkcie
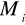
na każdej z krzywych cząstkowych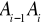
,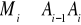
dla i=1,2,…,nwyznaczamy wektory
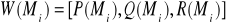
dla i=1,2,…,ntworzymy sumę
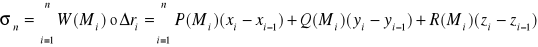
, gdzie „
” oznacza iloczyn skalarny wektorów.
Definicja
Jeśli przy ![]()
i ![]()
istnieje granica ![]()
niezależna od sposobu podziału krzywej i od wyboru punktów Mi, to granicę tę nazywamy całką krzywoliniową skierowaną funkcji W wzdłuż krzywej K i oznaczamy
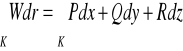
.
Uwagi
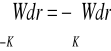
Jeśli krzywa
, jest zadana układem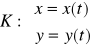
,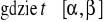
, a na krzywej K zadane jest płaskie pole wektorowe W o składowych [P,Q], to wtedy podobnie definiujemy całkę krzywoliniową skierowaną i oznaczamy ją
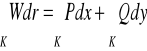
.
Jeśli
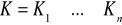
, gdzie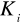
jest krzywą regularną dla i=1,…,n,
to definiujemy
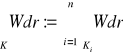
.
Twierdzenie (o zamianie całki krzywoliniowej skierowanej na całkę oznaczoną)
Niech K - krzywa regularna,
W - pole wektorowe ciągłe na krzywej ![]()
Wtedy
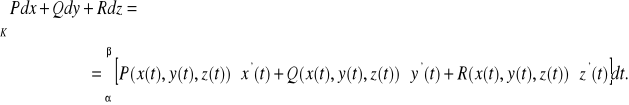
Uwaga
Jeśli krzywa K jest płaska, to
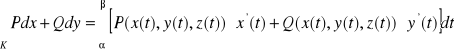
.
Interpretacja fizyczna
Niech K - krzywa skierowana od A do B,
W - pole sił na krzywej K.
Wtedy
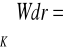
praca siły W wykonana przy przemieszczaniu masy jednostkowej wzdłuż krzywej K od punktu A do B.
Przykład (*)
Obliczyć całkę ![]()
po krzywej ![]()
skierowanej ujemnie względem swego wnętrza.
Zapiszmy równanie określające krzywą K w postaci równoważnej 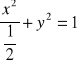
.
Jest to równanie elipsy.
Parametryzacja tej elipsy
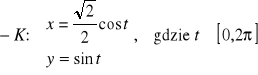
jest niezgodna z kierunkiem krzywej. Zatem
![]()
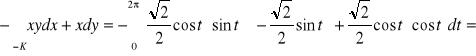
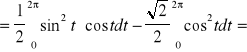
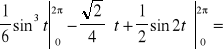
![]()
Definicja
Obszar płaski ograniczony jedną krzywą (Jordana) nazywamy jednospójnym, a obszar ograniczony p nieprzecinającymi się krzywymi obszarem p-spójnym.
obszar jednospójny obszar p-spójny
Umowa
Całkę krzywoliniową skierowaną po krzywej zamkniętej K oznaczamy też ![]()
.
Twierdzenie Greena
Z: Niech K - krzywa płaska zamknięta zorientowana dodatnio i ograniczająca obszar
jednospójny D,
P, Q - funkcje ciągłe mające ciągłe pochodne cząstkowe w obszarze D i na brzegu K.
T: 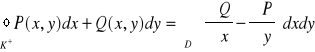
Przykład (*) c.d.
![]()
jest krzywą zorientowaną ujemnie, ![]()
,
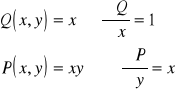
i z twierdzenia Greena otrzymujemy
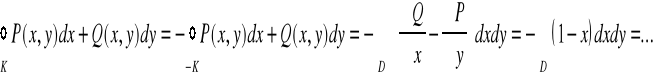
Zastosujemy uogólnione współrzędne biegunowe
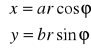
, gdzie a, b - stałe, ![]()
, ![]()
Jakobian powyższego odwzorowania wynosi![]()
.
W naszym przypadku wybieramy ![]()
, aby otrzymać obszar D ograniczony elipsą 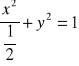
.Stąd
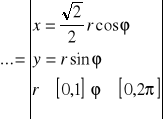
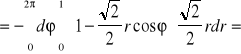
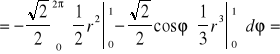
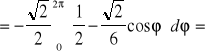
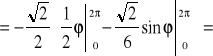
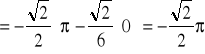
Twierdzenie (o niezależności całki krzywoliniowej od kształtu drogi całkowanej)
Z: Niech D - obszar jednospójny
P, Q - funkcje ciągłe, mające ciągłe pochodne cząstkowe w obszarze D
![]()
![]()
- krzywa regularna , ![]()
T: ![]()
- nie zleży od kształtu krzywej ![]()
a tylko od punktów A i B, t i wtedy oznaczamy ją 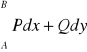
.
Dowód![]()
Niech ![]()
będą krzywymi regularnymi zawartymi w obszarze D, łączącymi punkty A i B, i skierowanymi od punktu A do B.
Wtedy krzywa ![]()
jest krzywą zamkniętą regularną, zorientowaną dodatnio, ![]()
. Oznaczmy przez ![]()
obszar jednospójny ograniczony przez krzywą C. Na podstawie twierdzenia Greena mamy
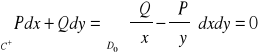
bo ![]()
, więc
![]()
![]()
![]()
![]()
Aby udowodnić implikację ![]()
wystarczy wykazać jej kontrapozycję, czyli udowodnić implikację
![]()
zależy od kształtu krzywej ![]()
.
Bez straty ogólności możemy założyć, że
![]()
.
Zatem
![]()
dla ![]()
.
Niech ![]()
będzie brzegiem koła ![]()
skierowanym dodatnio.
Wtedy na podstawie twierdzenia Greena mamy
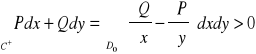
.
Stąd
![]()
,
czyli
![]()
.
Zatem całka po krzywej łączącej punkty A i B zależy od kształtu tej krzywej.
Wniosek
Niech D - obszar jednospójny,
C - krzywa zamknięta regularna, ![]()
,
![]()
- funkcje ciągłe mające ciągłe pochodne cząstkowe w D.
Wtedy
![]()
.
Całka różniczki zupełnej.
Niech D - obszar jednospójny,
![]()
.
Pytamy czy w obszarze D ![]()
, aby wyrażenie
![]()
było różniczką zupełną funkcji U w D ?
Oczywiście musi zachodzić![]()
i ![]()
.
Wtedy
![]()
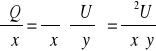
Z założenia
![]()
Zatem warunkiem koniecznym istnienia funkcji U jest równość
![]()
.
Stwierdzenie
Niech D - obszar jednospójny,
![]()
.
Wtedy
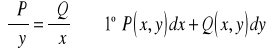
, jest różniczką zupełną funkcji U,
ponadto:
![]()
![]()
, gdzie![]()
,
![]()
- ustalony punkt
![]()
- punkt zmienny,
![]()
- krzywa regularna, ![]()
,
czyli
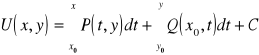
. (*)
![]()
![]()
dla dowolnej krzywej ![]()
.
Uzasadnienie wzoru (*)
Dla
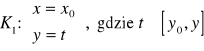
mamy ![]()
.
Podobnie dla

otrzymujemy ![]()
.
Stąd
![]()
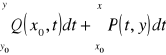
na podstawie twierdzenia o niezależności całki krzywoliniowej od kształtu drogi całkowania. Zatem
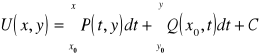
.
Uwaga
Wektor![]()
jest gradientem funkcji U, ![]()
.
Definicja
Funkcję U nazywamy potencjałem pola wektorowego W.
Przykład
Wykazać, że ![]()
jest różniczką zupełną pewnej funkcji ![]()
i wyznaczyć tę funkcję (potencjał).
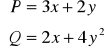
![]()
![]()
![]()
oraz ![]()
.
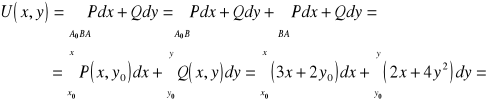
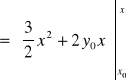
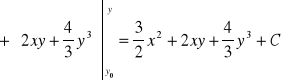
.
1
1
3
1
6
12
Wyszukiwarka
Podobne podstrony:
4.Całka różniczki zupełnej, MATEMATYKA, CAŁKI, CAŁKI KRZYWOLINIOWE I POWIERZCHNIOWE, 01Całki krzywol
ANALIZA MATEMATYCZNA CAŁKI KRZYWO LINIOWE
2.Całka krzywoliniowa nieskierowana, MATEMATYKA, CAŁKI, CAŁKI KRZYWOLINIOWE I POWIERZCHNIOWE, 01Całk
calki+krzywoliniowe, I semstr moje materiały, Matematyka 1 Semsetr, analiza mat zadania
3.Całka powierzchniowa zorientowana, MATEMATYKA, CAŁKI, CAŁKI KRZYWOLINIOWE I POWIERZCHNIOWE, 02Całk
LISTA 14 Całki krzywoliniowe
calki krzywoliniowe I i II rodzaju
03 2 Zastosowanie całki krzywoliniowej w mechanice
Całki krzywoliniowe
Sem 2. Wykład, Całki Krzywoliniowe
Całki, Analiza matematyczna
Całki krzywoliniowe i powierzchniowe, Mechatronika WAT, Matma, Inne notatki zadania itp
6643194-sciaga-calki, Studia, Matematyka, Analiza Matematyczna
więcej podobnych podstron