![]()
Akademia Techniczno - Humanistyczna
Wydział Budowy Maszyn i Informatyki
Zarządzanie i Inżynieria Produkcji
Rok 2, sem. 3
Ćwiczenie nr 40
Wyznaczanie współczynnika lepkości cieczy
metodą Stokesa.
Gr. nr 10
I Wstęp teoretyczny
Lepkość, zwana inaczej tarciem wewnętrznym, jest to właściwość płynów i plastycznych ciał stałych charakteryzująca ich opór wewnętrzny przeciw płynięciu. Lepkością nie jest jednak opór przeciw płynięciu powstający na granicy płynu i ścianek naczynia. Lepkość jest jedną z najważniejszych cech płynów (cieczy i gazów). Zgodnie z laminarnym modelem przepływu lepkość wynika ze zdolności płynu do przekazywania pędu pomiędzy warstwami poruszającymi się z różnymi prędkościami.
Parametrem charakteryzującym ciecz pod względem jej lepkości jest współczynnik lepkości dynamicznej oznaczony symbolem η. Definiuje go równanie Newtona, określające siłę tarcia wewnętrznego F występującą między warstwami cieczy poruszającej się ruchem laminarnym, działającym stycznie do powierzchni warstw.
![]()
gdzie: S - pole powierzchni styku trących o siebie warstw cieczy,
![]()
- gradient prędkości cieczy w kierunku prostopadłym do kierunku
przepływu cieczy, który określa zmianę prędkości cieczy pomiędzy dwoma warstwami oddalonymi o nieskończenie małą odległość dx
Do scharakteryzowania własności cieczy lepkich stosuje się także kinematyczny współczynnik lepkości v, czyli stosunek współczynnika lepkości dynamicznej, do gęstości cieczy:
![]()
gdzie:![]()
- gęstość cieczy lepkiej ,
![]()
współczynnik lepkości dynamicznej.
Wraz ze wzrostem temperatury, współczynnik lepkości η, spada. Lepkość cieczy związana jest z koniecznością pokonywania przez cząsteczki cieczy pewnej bariery energetycznej E między cząsteczkami podczas ruchu. Jako, że temperatura to nic innego, jak energia kinetyczna cząsteczek - jej wzrost ułatwia pokonanie bariery energetycznej. Wpływ temperatury na współczynnik lepkości określa się wzorem:
![]()
gdzie: k = 1,3805 ∙ 10-23 [J/K] jest stałą Boltzmana
T - temperatura w skali bezwzględnej Kelvina,
E - energia aktywacji przepływu lepkiego, jest to energia tworzenia wnęki cząsteczkowej, czyli miejsca w które przeskakuje dana cząsteczka opuszczając po wykonaniu pewnej liczby drgań, swoje poprzednie położenie
![]()
stała zależna od rodzaju cieczy.
Podczas ruchu z małymi prędkościami ciał stałych w cieczy lepkiej, kiedy ciecz opływa je w sposób warstwowy, ciała te doznają działania siły oporu, która jest uwarunkowana lepkością cieczy. Warstwy cieczy przylegające do ciała są unoszone razem z nim i dzięki tarciu wewnętrznemu pociągają za sobą kolejne warstwy położone w coraz dalszej odległości od ciała i poruszające się z coraz mniejszą prędkością. Wprawione w ruch warstwy cieczy działają hamująco na ciało wytwarzając wypadkowa siłę oporu T zwrócona przeciwnie
do kierunku jego ruchu i proporcjonalna do prędkości ciała v, wymiaru
liniowego l oraz współczynnika lepkości dynamicznej η:
T klv
Wartość tej siły dla kuli opisana jest wzorem Stokesa:
![]()
gdzie: T - siła oporu lepkiego
η - współczynnik dynamiczny lepkości cieczy
r - promień kuli
v - prędkość kuli
II Przebieg ćwiczenia, obliczenia oraz opracowanie wyników pomiaru
Przyrządy z których korzystaliśmy w tym ćwiczeniu to:
wiskozymetr Stokesa
ultratermostat
termometr elektroniczny
śruba mikrometryczna
kulki stalowe
stoper
waga laboratoryjna i analityczna
Na początku ćwiczenia sprawdziliśmy poziom wody w ultratermostacie i dolaliśmy wody do pełna zbiornika. Włączyliśmy ultratermostat i rozpoczęliśmy pomiar czasu spadania kulki między ustalonymi liniami na wiskozymetrze. Rozpoczęliśmy pomiar od 22.6 ºC.
Odległość między liniami wiskozymetru wynosiła l=50 cm±0.5 cm. Powtórzyliśmy pomiar w tej temperaturze dla 4 kolejnych kulek. Następnie włączyliśmy grzałkę termostatu i nagrzewając kolejno do temperatur 25ºC, 30ºC, 35ºC, 40ºC, 45ºC, 50ºC mierzyliśmy czas opadania 5 kulek. Zamieniliśmy wartości temperatur w których odbywały się pomiary na wartości w skali bezwzględnej, a następnie obliczyliśmy ich odwrotności 1/T [1/K]. Wyniki wpisaliśmy do tabeli 1.
Tabela 1
Nr pomiaru |
Temp. [C] |
Temp. [K] |
1/T [K] |
t1 [s] |
t2 [s] |
t3 [s] |
t4 [s] |
t5 [s] |
<t> [s] |
1 |
22.6 |
295.6 |
33,82 |
4.71 |
4.78 |
4.78 |
4.81 |
4.75 |
4.77 |
2 |
25 |
298 |
33.56 |
4.21 |
4.06 |
4.21 |
4.00 |
4.06 |
4.11 |
3 |
30 |
303 |
33.00 |
3.21 |
3.12 |
3.12 |
3.09 |
3.15 |
3.14 |
4 |
35 |
308 |
32.46 |
2.68 |
2.62 |
2.65 |
2.62 |
2.62 |
2.64 |
5 |
40 |
313 |
31.95 |
2.28 |
2.25 |
2.31 |
2.34 |
2.28 |
2.29 |
6 |
45 |
318 |
31.45 |
2.00 |
2.00 |
1.96 |
2.00 |
1.96 |
1.98 |
7 |
50 |
323 |
30.96 |
1.75 |
1.75 |
1.78 |
1.84 |
1.78 |
1.78 |
Do tabeli 1 wpisaliśmy także średnie czasy opadania kulki dla poszczególnych temperatur zgodnie ze wzorem:
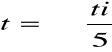
Następnie zmierzyliśmy średnicę 5 wybranych kulek z pomocą śruby mikrometrycznej. Na podstawie średnicy kulek obliczyliśmy średnią średnice kulki oraz średni błąd kwadratowy pojedynczego pomiaru średnicy Sd skorygowany przez współczynnik studenta (wartość odczytana z tablic dla n=5 i α=0.7) i błąd bezwzględny pomiaru średnicy kulki
. Wyniki wpisaliśmy do tabeli 2.
Tabela 2
d1 [ |
d2 [ |
d3 [ |
d4 [ |
d5 [ |
<d> [ |
Sd [ |
|
2.49 |
2.48 |
2.50 |
2,49 |
2,50 |
2,49 |
0,01 |
0,014 |
Obliczyliśmy mase M 10 kulek jako średnią arytmetyczną mas M1 i M2, oraz błąd pomiaru masy ΔM.
Obliczyliśmy masę m jednej kulki, a jej błąd oszacowaliśmy jako Δm = ΔM/10. Wyniki wpisaliśmy do tabeli 3.
Tabela 3
M1 [ |
M2 [ |
M [ |
ΔM [ |
m [ |
Δm [ |
649.1 |
650.3 |
649.7 |
0.6 |
64.97 |
0.06 |
Wprowadziliśmy wyniki pomiarów i obliczeń zgromadzone w tabelach 1-3 do programu komputerowego. Wprowadziliśmy wartości gęstości roztworu gliceryny wykorzystując dane z tab.5 zamieszczonej na ostatniej stronie instrukcji. Gęstość w temperaturze początkowej ustaliliśmy metodą interpolacji liniowej. Program obliczył nam
. Wyniki obliczeń wpisaliśmy do tabeli 4.
Tabela 4
Nr |
Temperatura [C] |
Temperatura [K] |
1/T [K] |
η [Ns/m2] |
Δη [Ns/m2] |
Lnη [-] |
1 |
22.6 |
295.6 |
33.80 |
0.220 |
0.015 |
-1.516 |
2 |
25 |
298 |
33.50 |
0.189 |
0.015 |
-1.664 |
3 |
30 |
303 |
33.00 |
0.145 |
0.013 |
-1.933 |
4 |
35 |
308 |
32.50 |
0.122 |
0.012 |
-2.106 |
5 |
40 |
313 |
31.90 |
0.106 |
0.012 |
-2.247 |
6 |
45 |
318 |
31.44 |
0.092 |
0.012 |
-2,391 |
7 |
50 |
323 |
30.96 |
0.082 |
0.011 |
-2,499 |
![]()
Program obliczył nam wartości parametrów a i b prostej regresji oraz ich błędów pomiarowych. Z równania wynika zależność liniowa (y=ax+b) co oznacza że:
a= ![]()
b= [1]
Natomiast wartości jakie podał nam program komputerowy wyniosły:
a = 3380[K]
Δa = 220[K]
b = -13.02[-]
Δb = 0.72[-]
Następnie obliczyliśmy energie aktywacji przepływu lepkiego E oraz błąd bezwzględny ΔE zgodnie ze wzorami:
E= a*k
k= 1.3805*10-23 [J/K]
E= 3380 * 1.3805*10-23 = 46.7*10-21 [J]
![]()
ΔE= Δa*k
ΔE= 220 * 1.3805*10-23 = 3.0*10-21 [J]
![]()
Zamieniamy uzyskaną energię w dżulach na elektronowolty wiedząc że
1 eV = 1.6*10-19 [J]
E= 46.7*10-21 [J] / 1.6*10-19 [J]= 29.18*10-2 eV = 0.292 eV
ΔE= 3.0*10-21 [J] / 1.6*10-19 [J] = 1.875*10-2 eV = 0.019 eV
Obliczyliśmy współczynnik lepkości dynamicznej dla temperatury 303 [K] według wzoru:
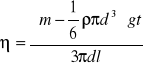
gdzie: ![]()
- gęstość roztworu gliceryny w temperaturze 303 [K]
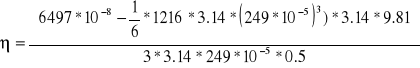
![]()
wyprowadzenie jednostki:
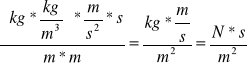
![]()
Obliczyliśmy błąd bezwzględny lepkości dynamicznej dla temperatury 303 [K[ według wzoru:
![]()
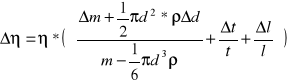
lecz przed podstawieniem do wzoru potrzebowaliśmy obliczyć Δt i obliczyliśmy to ze wzoru:
![]()
z tym że ![]()
lecz musieliśmy skorzystać wczesniej ze wzoru:
St=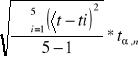
St= 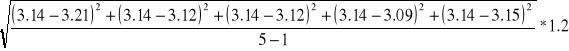
St= 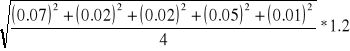
St= 0.0027s = 0.003 s
![]()
![]()
![]()
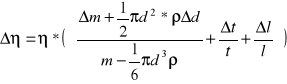
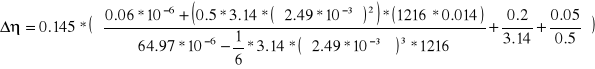
![]()
Mamy obliczone parametry a i b oraz zależność ![]()
więc uzupełniliśmy tabele 4 o nt dla poszczególnych czasów:
a = 3380 [K]
a= ![]()
b = -13.02[-]
b= ![]()
e =2.72
eb =![]()
![]()
![]()
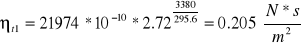
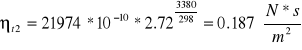
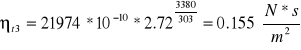
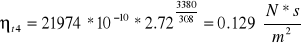
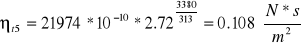
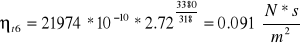
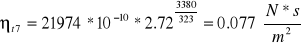
Uzupełniliśmy tabele 4
Nr |
Temperatura [C] |
Temperatura [K] |
1/T [K] |
η [ |
Δη [ |
Lnη |
|
|
|
|
|
|
|
|
|
1 |
22.6 |
295.6 |
33.8 |
0.220 |
0.015 |
-1.516 |
0.205 |
2 |
25 |
298 |
33.5 |
0.189 |
0.015 |
-1.664 |
0,187 |
3 |
30 |
303 |
33.0 |
0.145 |
0.013 |
-1.933 |
0,155 |
4 |
35 |
308 |
32.50 |
0.122 |
0.012 |
-2.106 |
0,129 |
5 |
40 |
313 |
31.90 |
0.106 |
0.012 |
-2.247 |
0,108 |
6 |
45 |
318 |
31.44 |
0.092 |
0.012 |
-2,391 |
0,091 |
7 |
50 |
323 |
30.96 |
0.082 |
0.011 |
-2,499 |
0,077 |
III Wnioski
Ćwiczenie pozwoliło nam zbadać zależność lepkości cieczy od temperatury. Lecz wystąpiły błędy poprzez różny czas reakcji oraz co spowodowało odchylenie od prawidłowych wartości.
![]()