WYNIKI Z ROZWIĄZANIAMI

Ad 1)

Wzór na międzynarodowy efekt Fishera

W naszym przypadku można go zapisać jako

znamy

kurs bieżący s₀ =2,8250

roczną stopę % w Polsce i_PLN =5,5 %

roczną stopę % w Australii i_AUD =2,5%

a szukamy s_t

dlatego przekształcamy wzór do postaci

a podstawiając nasze dane uzyskujemy następujący wynik

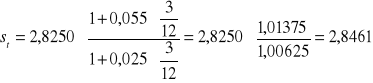
Uwaga: roczną stopę procentową należy sprowadzić do stopy na 3 miesiące i dlatego mnożymy ją przez 3/12

ODPOWIEDŹ:

Zgodnie z międzynarodowym efektem Fishera prognozowany kurs za 3 miesiące wyniesie 2,8461

Zad 2)

zasada względnego parytetu siły nabywczej może zostać wyrażona wzorem

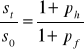
z treści zadania znamy

kurs bieżący (s₀) 1,2400

kurs prognozowany za rok (s_t) 1,2370

prognozę inflacji w USA na ten okres roczny (p_f) 1%

nie znamy prognozy inflacji dla Szwajcarii (p_h) ?

(Uwaga: !!

W naszym wzorze przyjmujemy założenie, że poziom inflacji (p_h) odnosi się do inflacji w kraju waluty notowanej a poziom inflacji (p_f) odnosi się do inflacji w kraju waluty bazowej.

Jeśli więc mamy kurs USD/CHF gdzie dolar jest walutą bazową a frank walutą notowaną to inflację w USA oznaczymy jako p_f a inflację w Szwajcarii jako p_h)

Aby obliczyć (p_h) przekształcamy powyższy wzór

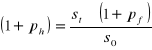
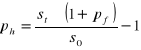
Podstawiamy nasze dane do wzoru

ODP: Aby przy wykorzystaniu względnej teorii parytetu siły nabywczej dokonać prognozy kursu USD/CHF na poziomie 1,2370 należało przyjąć założenie, że w Szwajcarii inflacja wyniesie w analizowanym okresie 0,76%.

Ad 3)

Znamy następujące notowania

Bank A podaje kurs EUR/USD 1,2320 (kupno) 1,2400 (sprzedaż)

Bank B podaje kurs USD/EUR 0,8020 (kupno) i 0,8050 (sprzedaż)

Aby je porównać należy przekształcić np. kursy w Banku B w odwrotne

Po przekształceniu otrzymujemy notowania w Banku B

EUR/USD 1,2422 (kupno) i 1,2469 (sprzedaż)

ODP : W związku z tym możemy dokonać zyskownego arbitrażu, gdyż możemy kupić euro taniej w banku A, a sprzedać drożej w banku B.

Za 1000 dolarów kupimy w banku A

W banku B sprzedamy euro za

ODP: Na arbitrażu zarobimy więc 1,77dolara

4)

mamy następujące informacje:

USD/PLN
3,9250 3,9300

USD/SEK
7,3500 7,4500

Mamy obliczyć kurs krosowy

Rozwiązanie:

Kurs krosowy SEK/PLN otrzymamy w wyniku podzielenia USD/PLN przez USD/SEK, ponieważ:

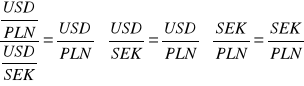
pamiętamy ponadto, że

1.kurs kupna musi być mniejszy od kursu sprzedaży, oraz

2.kurs kupna ma być to kombinacja dająca możliwie najmniejszy kurs

3.kurs sprzedaży ma być kombinacją dającą możliwie największy kurs

dlatego

kurs kupna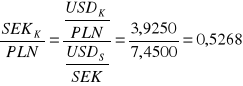

kurs sprzedaży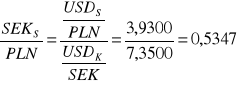

ODP: SEK/PLN 0,5268 0,5347

5)

Mamy następujące notowania rynkowe

(w banku A) USD/CHF 1,2730

(w banku B) USD/PLN 3,9210

(w banku C) CHF/PLN 3,0150

Aby sprawdzić, czy jest możliwy arbitraż między CHF i PLN obliczamy kurs krosowy CHF/PLN na podstawie notowań

USD/CHF 1,2730

USD/PLN 3,9210

Kurs obliczymy dzieląc USD/PLN przez USD/CHF ponieważ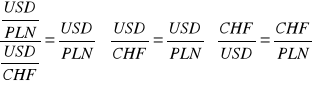

A w związku z tym wyniesie on

Wynika, z tego, że frank szwajcarski jest tańszy w banku C niż poprzez dwie transakcje w banku A i B.

ODP: stwierdzona różnica stwarza okazję do arbitrażu

Arbitraż obliczamy w sposób następujący

1) kupujemy CHF w banku C po kursie 3,0150

za 1000 zł otrzymujemy więc 331,67 franków

2) za CHF kupujemy USD w banku A

za 331,67 franków otrzymujemy 260,54 dolarów

3) za USD kupujemy PLN w banku B

ODP: ostatecznie otrzymujemy 1021,58 zł czyli o 21,58zł więcej niż mieliśmy na początku. Jest to nasz zysk arbitrażowy

6)

USD/PLN po deprecjacji o 5% wynosi obecnie 3,9240

Wiemy, że deprecjację waluty notowanej obliczamy ze wzoru

znamy

s₁=3,9240

d/a _{waluty notowanej} = -5%

chcemy obliczyć s₀

Przekształcamy powyższy wzór

i podstawiamy nasze dane

ODP: Kurs przed deprecjacją złotego wyniósł 3,7278

Znając kurs przed zmiana i po zmianie możemy obliczyć aprecjację USD z wzory na stopę deprecjacji/aprecjacji waluty bazowej

ODP: Aprecjacja USD wyniosła 5,26%

7)

Ze wzoru na parytet stóp %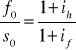

Otrzymujemy wzór na kurs terminowy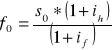

jako, że znamy

kurs spot EUR/PLN 4,8730 (s₀)

roczna stopa % w Polsce 5,3% (i_h)

roczna stopa % w EUM 2,4% (i_f)

to na podstawie powyższego wzoru możemy obliczyć kurs terminowy f₀

w tym celu musimy roczne stopy % dostosować do długości kontraktu terminowego; w naszym przypadku mnożymy je przez 9/12 (ponieważ długość kontraktu wynosi 9 miesięcy)

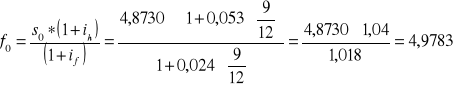
ODP: Kurs terminowy EUR/PLN na 9 miesięcy wyniesie 4,9783

8)

Ze wzoru na parytet stóp %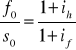

Otrzymujemy wzór na kurs terminowy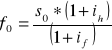

jako, że znamy

kurs spot EUR/USD 1,2080

roczna stopa % w EUM 2,3% (nasze i_f)

roczna stopa % w USA 2,0% (nasze i_h)

to na podstawie powyższego wzoru możemy obliczyć kurs terminowy f₀

(UWAGA !

i_h - jest to stopa % waluty notowanej

i_f - jest to stopa % dla waluty bazowej)

w celu obliczenia kursu terminowego musimy roczne stopy % dostosować do długości kontraktu terminowego; w naszym przypadku przemnożymy je przez 6/12 (ponieważ długość kontraktu wynosi 6 miesięcy)

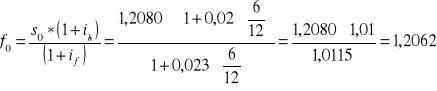
ODP: Kurs terminowy EUR/USD na 6 miesięcy wyniesie 1,2062

---