MACIERZE:

A- macierz wym. m (wiersze)* n (kolumny)

D_ij=(-1)^i+j * det. A_ij det.A=det.A^T

(A^T)^T=A A*A^-1= I

Macierz osobliwa: det. A = 0

Macierz nieosobliwa: det. A≠0

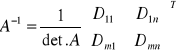
Metoda przekształceń elementarnych:

Rozwiązanie układu równań liniowych:

gdzie:

A-macierz główna ukł. równań

X-macierz niewiadomych

B-macierz wyrazów wolnych

Układ CRAMERA (ma jedno rozw.):

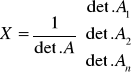
CZYLI:

Rozwiązanie ukł. równań:

LICZBY ZESPOLONE:

Liczba zespolona: Z=(x,y) Suma:Z₁+Z₂=(x₁+x₂, y₁+y₂)

Iloczyn l. zesp. : Z₁*Z₂=( x₁*x₂, y₁*y₂)

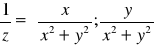
Jednostka urojona:

!!!!!!!!!!! i=(0,1) ALE! i²=-1 !!!!!!!!!!!

Postać algebraiczna liczby zespolonej:

Re(z) = a Im(z) = b

Postać algebraiczna sprzężenia liczby zespolonej:

Interpretacja geometryczna (zakreskowala część na układzie współrzędnych XY):

1)Okrąg

2)Koło

3)Powierzchnia poza kołem

4)Środek odległości miedzy z₁ a z₂

5)Strona z₁ od środka

6)Strona z₂ od środka

Argumenty liczby zespolonej:

Postać trygonometryczna liczby zespolonej:
z = r (cosφ+sinφ) r = |z|

Mnożenie liczb zespolonych w postaci trygonometrycznych:

Dzielenie liczb zespolonych w postaci trygonometrycznej:

Wzór de Moire'a:

Pierwiastek liczby C

GEOMETRIA ANALITYCZNA

Suma wektorów:

Długość wektora :

Iloczyn skalarny:

Iloczyn wektorowy:

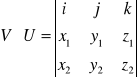
Równania płaszczyzn:

P0=(x0,y0,z0) wektor wodzący n=(A,B,C)

Normalne: Ogólne:

Π: A(x-x₀)+B(y-y₀)+C(z-z₀) Π: Ax+By+Cz+D

Parametryczne: Odcinkowe:

x=x₀+sa₁+ta₂

y=y₀+sb₁+tb₂

z=z₀+sc₁+tc₂

CIĄGI

Równania prostej w przestrzeni R³:

Parametryczne: Kierunkowe:

x=x₀+ ta

y=y₀+ tb

z=z₀+ tc

Odległość między płaszczyznami:

CIĄGI:

Ciąg Fibonacciego: C_n+2=C_n+C_n+1

GRANICE

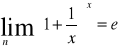
POCHODNE

1. (liczba)'=0 (x)'=1

2.(xⁿ)' = n*x^n-1

3.(sinx)'=cosx

4.(cosx)'=-sinx

5.

6.

7.

8.

9.

10.

11.(a^x)'=a^x lna

12.(e^x)'=e^x

13.

14.

---