1.4. ELEMENTARNE WIADOMOŚCI Z TEORII BŁĘDÓW

Doświadczalne wyznaczenie wartości liczbowych pewnej wielkosci nazywamy pomiarem tej wielkości, a pomierzoną wartość spostrzeżeniem. Zakładając jednolity układ jednostek dla ustalonej metody pomiarowej, stwierdzamy w doświadczeniach, że wyniki naszych pomiarów nie będą dostatecznie ścisłe, to znaczy bezbłędne.

Mniejsze lub większe niezgodności kilkakrotnego pomiaru tej samej wielkości spowodowane są tym, że każde nasze pojedyncze spostrzeżenie obarczone jest mniejszym lub większym błędem. Niedoskonałość naszych zmysłów, ograniczona precyzja budowy przyrządów pomiarowych, którymi wykonujemy obserwacje, oraz zmienność środowiska w czasie trwania pomiarów są najistotniejszymi przyczynami pojawienia się tych błędów. Analiza rodzaju i przyczyn powstawania źródeł błędów, należące do teorii błędów, staje się podstawą wnikliwszego opracowania wyników obserwacji.

Zarówno spostrzeżenie, jak i jego błąd nazywamy w rachunku prawdopodobieństwa zmienną losową, przyjmującą w wyniku doświadczenia pewną liczbę rzeczywistą z pewnym prawdopodobieństwem. Dla scharakteryzowania zmiennej losowej musimy znać zbiór tych liczb, które ona może przyjmować, oraz wiedzieć, jak często zmienna ta może przyjmować różne swe wartości. Spostrzeżenia czy błędy spostrzeżeń traktujemy jako realizację zmiennej losowej. W teorii błędów czynimy założenia, że wynik obserwacji lub jego błędy są zmienną losową natury ciągłej - przybierające dowolne wartości liczbowe, należące do pewnego przedziału liczbowego, lub natury dyskretnej - przybierające wartości skokowe. Występujące błędy przy pomiarach dzielimy, ze względu na źródło ich powstania i istotę, na trzy rodzaje, a mianowicie: błędy grube, systematyczne i przypadkowe.

1.4.1. Charakterystyka błędów pomiarów

A. Istota powstawania błędów

Pomiary lub obserwacje dzielą się na:

a) jednakowo dokładne czyli takie, które dokonywane są w jednakowych warunkach, jednym i tym samym narzędziem oraz przez jednego i tego samego obserwatora;

b) niejednakowo dokładne - takie, które przeprowadzane są w różnych warunkach, przy użyciu różnych narzędzi lub wykonywane przez różnych obserwatorów, itp.

Różnica między jakimkolwiek wynikiem pomiaru i rzeczywistą wartością wielkości mierzonej nosi nazwę błędu prawdziwego. Błędów tych z reguły nie można wyznaczyć, ponieważ rzeczywista wartość mierzonej wielkości pozostaje nieznana. W praktyce zatem błędy pomiarów wyznacza się względem najbardziej prawdopodobnej wartości mierzonej wielkości. Błędy te nazywamy błędami pozornymi.

Rozróżniamy trzy następujące grupy błędów:

a) Błędy grube czyli takie, których bezwzględne wartości przekraczają granice dokładności pomiarów. Do nich zaliczne są omyłki obserwatora oraz błędy nie odpowiadające dokładności pomiarów w danych warunkach. Typowym przykładem może być odczyt koła poziomego teodolitu wynoszący 67, zamiast 76. Podobnie przy pomiarze boku poligonowego taśmą - przez zgubienie jednej szpilki możemy zrobić błąd wartości jednego przyłożenia taśmy.

Błędy grube można łatwo zauważyć w danej grupie pomiarów i sprawdzić przez wykonanie powtórnych pomiarów kontrolnych. Dlatego w rachunku wyrównawczym (zajmującym się przede wszystkim opracowaniem wyników pomiarów) tego typu błędami nie zajmujemy się, zakładając z góry, że muszą one być wyeliminowane z wszelkich rozważań.

b) Błędy systematyczne to takie,które zniekształcają wy- niki pomiarów według określonego prawa.Na przykład przesunięcie tarczy azymutalnej kompasu względem igły magnetycznej powoduje powstanie błędu systematycznego określanych kierunków. Błędy systematyczne mogą być zmienne typu narastającego, jednoronne, periodyczne, stałe i mieszane.

Błędy zmienne typu narastającego mogą powstawać na przykład, podczas mierzenia odcinkami odległości na mapie.

Błędy jednostronne mają zmienne wartości bezwzględ ne, ale zniekształcają wyniki pomiarów w jednym kierunku. Przykładem błędów jednostronnych są błędy azymutów określanych ponownie po pewnym czasie, gdy poprawka żyrokompasu zniemiła się liczbowo.

Błędy systematyczne periodyczne są to takie błędy, które zmieniają się według znanych zależności, nie tylko swoją wartość, ale i znak. Przykładem takiego błędu może być błąd określenia azymutu spowodowany mimośrodem celu.

Błędami stałymi nazywamy takie błędy, które przy każdym pomiarze pozostają niezmienne pod względem wartości bezwzględnej i znaku.

Błędy mieszane to błędy, których błąd systematyczny jest częścią składową błędu przypadkowego.

Błędy systematyczne, zależne od indywidualnych cech zmysłów obserwatora (wzrok, słuch,...) nazywają się błędami osobowymi.

c) Błędy przypadkowe są to takie błędy, których przyczyny zależą od okoliczności zmieniających się w czasie między poszczególnymi pomiarami. Błędy te posiadają następujące zasadnicze własności:

-błędy posiadające równe wartości bezwzględne ale przeciwne znaki są jednakowo prawdopodobne;

-błędy duże są mniej prawdopodobne, niż błędy małe;

-w określonych warunkach prawdopodobieństwo powstania błędów przekraczające pewne granice jest stosunkowo mało;

-wewnątrz tych granic błędy przypadkowe mogą przyjmować dowolne wartości;

-przy zwiększaniu liczby pomiarów tej samej wielkości suma błędów przypadkowych dąży do zera.

Powyższe własności błędów przypadkowych powstają tym częściej, im większa jest liczba pomiarów. Rozkład błędów zgodnie z podanymi wyżej podstawowymi wartościami nosi nazwę normalnego.

B. Pojęcie błędów przypadkowych

Rachunek wyrównawczy posługuje się głównie błędami przypadkowymi, zakładając, że wyeliminowaliśmy ze spostrzeżeń błędy grube i systematyczne, a procesowi wyrównania będziemy poddawać spostrzeżenia obarczone jedynie błędami przypadkowymi.

Pojęcie błędów przypadkowych definiowane jest w rachunku prawdopodobieństwa za pomocą wartości przeciętnej (patrz p. 1.4.2). Błędy nazywamy przypadkowymi, jeżeli ich wartość przeciętna

E() = 0 (1.21)

to znaczy, że

(1.22)

Do grupy błędów przypadkowych należą błędy prawdziwe i błędy pozorne, którymi zajmuje się rachunek wyrównawczy. Zanim zostanie określona ich definicja, należy ustalić, co trzeba rozumieć pod pojęciem wielkości prawdziwej i wielkości prawdopodobniej.

Jeżeli w wyniku pomiaru istnieje możliwość dokładnego ustalenia mierzonego zjawiska, to jego wartość liczbową X nazwywamy wielkością prawdziwą. Również za wielkość prawdziwą możemy uznać (w niektórych okolicznościach) wartość uzyskaną z pomiarów bardzo dokładnych w stosunku do pomiarów charakteryzujących się niższą dokładnością. Tak na przykład wynik pomiaru długości odcinka precyzyjnym dalmierzem elektrooptyczmym może być traktowany jako prawdziwy, w stosunku do pomiaru tego odcinka wykonanego na przykład taśmą stalową. W wyniku n-krotnego powtórzenia obserwacji nad wielkością prawdziwą otrzymujemy ciąg wartości, skupionych swymi wartościami liczbowymi wokół prawdziwej wartości. Zatem, mierząc wielkość prawdziwą X popełniamy pewne nieznaczne błędy niezależnie od naszej woli. Błędy te będziemy nazywać błędami prawdziwymi. Powyższe zależności ujmiemy równością

(1.23)

gdzie: X - wielkość prawdziwa,

- spostrzeżenia (dla i = 1,2, ... , n),

- błąd prawdziwy i-tego spostrzeżenia

lub

(1.24)

Jeżeli w równości (1.23) wartość prawdziwa X nie jest znana, zastępujemy ją wielkością uznaną przez nas za najlepszą (najprawdopodobniejszą). Taką wartość otrzymujemy przez wielokrotne powtórzenie doświadczenia i odpowiednie wyrównanie ich wyników, co zbliża tę wartość prawdopodobną do wartości prawdziwej. Wtedy tak obliczony błąd z wartości najbardziej prawdopodobniej nazywamy błędem pozornym.

Między tymi wartościami istnieje następująca zależność:

(1.25)

gdzie:
- wielkość najbardziej prawdopodobna,

- spostrzeżenia (dla i = 1,2, ... , n),

- poprawka i-tego spostrzeżenia.

Równość (1.25) napisana w formie

(1.26)

jest najprostszą postacią równań, znanych pod nazwą równań poprawek lub obserwacyjnych, a niekiedy pod niewłaściwą nazwą równań błędów.

Podstawienie do prawej strony równości (1.23) wartości
wyznaczonej z (1.25) daje równość

(1.27)

Powyższa równość wskazuje, że wielkość
- jako poprawiająca spostrzeżenie - by osiągnęła swój cel, musi mieć znak przeciwny niż błąd prawdziwy. Jeżeli wielkość
zdąża do wartości X, to i v jako błąd pozorny zdąża do błędu prawdziwego. Rachunek wyrównawczy posłguje się w praktyce głównie błędami pozornymi jako błędami przypadkowymi.

1.4.2. Rozkład normalny błędów przypadkowych

A. Charakterystyka zmiennej losowej

W teorii błędów rozważa się jako zmienną losową błąd przypadkowy pomiaru. Mogą nią być np. odchyłki zamknięć w sieci poligonowej.

Zmienna losowa jest dostatecznie scharakteryzowana, jeżeli znamy jej rozkład i parametry tego rozkładu.

Przyporządkowanie każdej wartości x tej zmienne jej prawdopodobieństwa nazywamy rozkładem zmiennej losowej skokowej, co zapisujemy

dla i = 1,2,... (1.28)

przy czym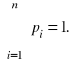

Tabela 1.1

x	x1	x2	..............	xn
p(x)	p1	p2	..............	pn

Tabelę 1.1 nazwywamy tabelą rozkładu zmiennej losowej skokowej.

Funkcję rozkładu zmiennej losowej ciągłej nazywamy prawdopodobieństwo tego zdarzenia, że zmienna losowa x przyjmie wartość spełniającą nierówność

(1.29)

Funkcję rozkładu oznaczamy symbolem

Prawdopodobieństwo
jest funkcją x, i oznaczamy je przez F(x)

= F(x) (1.30)

Funkcja F(x) nosi nazwę dystrybuanty zmiennej losowej.

Dystrybuanta jest funkcją nie malejącą dla dowolnej zmiennej losowej, posiadającą wartości

oraz
(1.31)

czyli, że

= 1 - 0 = 1

Jeżeli wszystkie wartosci zmiennej losowej zawierają się w przedziale [a, b] to na lewo od punktu a F(x) = 0, a na prawo od b F(x) = 1. Dla zmiennej losowej ciągłej dystrybuanta jest również ciągła. Jeżeli dystrybuanta zmiennej losowej ma pochodną w punkcie x, to pochodna ta nazywa się gęstością prawdopodobieństwa zmiennej losowej w punkcie x. Oznaczając gęstość prawdopodobieństwa przez (x), napiszemy

(1.32)

Z wzorów (1.23) i (1.25) wynika, że

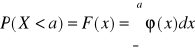
oraz

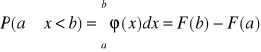
Zmienną losową można scharakteryzować w przybliżony sposób, podając pewne parametry opisowe. Do najczęściej używanych parametrów w teorii błędów należą: wartość oczekiwana, odchylenie przeciętne, wariancja i odchylenie standardowe.

Wartością oczekiwaną lub wartością średnią (nadzieją matematyczną) zmiennej losowej ciągłej x nazywa się całkę

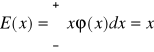
(1.33)

Jeżeli we wzorze (1.26) wszystkie wartości w przedziale (x,x+dx) można uważać za równe x, a prawdopodobieństwo takich wartości (x)dx = p, to zastępując znak całki sumą, otrzymamy

(1.34)

Wzór (1.34) określa wartość oczekiwaną zmiennej losowej skokowej. Ten sam wzór określa również empiryczną wartość oczekiwaną dla zmiennych losowych ciągłych.

W rachunku wyrównawczym wartość (1.34) identyfikuje się ze średnią arytmetyczną. Niech
(dla i = 1,2,...,n), wówczas

Znajomość wartości przeciętnej zmiennej losowej nie wystarczy do przedstawienia rozkładu wartości tej zmiennej względem jej wartości przeciętnej. Możemy to scharakteryzować za pomocą wartości odchyleń.

Odchyleniem wartości zmiennej losowej od wartości przeciętnej tej zmiennej będziemy nazywać różnicę

Z = X - E(x) (1.35)

Odchyleniem przeciętnym zmiennej losowej skokowej nazywamy przeciętną wartość bezwzględnych odchyleń wartości zmiennej losowej od jej wartości przeciętnej, co w przyjętych oznaczeniach zapiszemy

(1.36)

Dla zmiennej losowej ciągłej odchylenie przeciętne oblicza się przez całkowanie

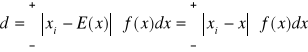
(1.37)

W rachunku wyrównawczym wartość przeciętną zmiennej losowej utożsamia się z wartością średnią (przy jednakowych prawdopodobieństwach). Natomiast wariancją zmiennej losowej x nazywa się wartość przeciętną kwadratu odchylenia tej zmiennej od wartości przeciętnej E(x)

(1.38)

gdzie V(X) jest używanym oznaczeniem wariancji.

Dla zmiennej losowej ciągłej wariancja wyrażona jest wzorem

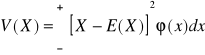
(1.39)

Dla zmiennej losowej skokowej wariancję zapiszemy w postaci

(1.40)

Przy obliczaniu wariancji korzysta się często ze związku

(1.41)

Odchylenie standartowe jest to pierwiastek kwadratowy z wariancji

(1.42)

B. Podstawowe wiadomości o rozkładzie normalnym

Spotykane w praktyce zmienne losowe ciągłe bardzo często posiadają rozkład normalny. Rozkład normalny jest uzasadnionym modelem matematycznym błędów przypadkowych.

Funkcja gęstości (x) rozkładu normalnego określona jest wzorem

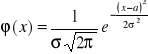
(1.43)

gdzie: i a - parametry rozkładu,

- stosunek obwodu koła do średnicy,

e - zasada logarytmów naturalnych.

Dla lepszego zrozumienia problemu musimy przede wszystkim wyjaśnić znaczenie parametrów a i . Ze wzoru (1.36) wynika, że krzywa y = (x) osiąga maksimum dla x=a

(1.44)

Wartość parametru zawsze > 0 powoduje zmianę kształtu krzywej rozkładu. Ze wzrostem wartość y maleje, a ponieważ pole ograniczone krzywą i osią odciętych jest równe jedności na mocy wzoru

.

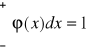
Ze wzrostem krzywa rozszerza się wzdłuż osi 0 X. Odwrotnie, przy zmiejszaniu się krzywa wydłuża się w kierunku pionowym, a zwęża się w kierunku poziomym.

Na rys.1.3 są przedstawione wykresy rozkładów nomalnych dla różnych wartości a i tej samej wartości . Wartość a jest środkiem zgrupowania rozkładu i jeśli się zmienia a, to krzywa (x) przesuwa się wzdłuż osi x, nie zmieniając przy tym kształtu.

Rys. 1.3

Rys. 1.4

Odwrotnie jest na rys.1.4, gdzie dane są wykresy dla a = 0 i różnych wartości . Mamy zbiór krzywych normalnych scentrowanych, zależnych tylko od jednego parametru. Na rys. (1.3) i (1.4) widać, że krzywe gęstości są nieograniczone (
), symetryczne względem x = a i posiadają po dwa punkty przegięcia, oraz wielkość ich pól ograniczonych krzywymi nie zależy od parametrów.

W obliczeniach posługujemy się nieco inną postacią funkcji. Wprowadzamy nową zmienną, zwaną zmienną standaryzowaną (umowną)

(1.45)

otrzymamy wtedy

(1.46)

lub

(1.47)

gdzie

(1.48)

Równość (1.41) jest rozkładem normalnym standardowym, to znaczy o zerowej wartości (oczekiwanej) a i jednostkowej wartości . Jest ona stabelaryzowana i dla żądanych wartości odczytuje się wartość funkcji gęstości. Rozkład normalny standardowy zapisuje się umownie N(0,1).

W rachunku wyrównawczym używa się nieco innej postaci funkcji gęstości rozkładu normalnego, zwanej funkcją Gaussa, spełniającej wszystkie własności rozkładu ogólnego. W miejsce parametru wprowadzono parametr h, zwany miarą dokładności. Między tymi wielkościami istnieje udowodniony związek, a mianowicie

(1.49)

Podstawiając (1.49) do (1.43) otrzymujemy

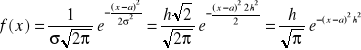
(1.50)

Jeżeli w wykładniku funkcji zastąpimy x - a przez wartość błędu , otrzymamy funkcję, zwaną funkcją Gaussa

(1.51)

Wykres funkcji gęstości (1.51) przestawiono na rys.1.5.

Rys. 1.5

Wartości odłożone są na osi odciętych, zaś () na osi rzędnych. Dla = 0 () jest osią symetrii. Krzywa funkcji gęstości y = () osiąga maksimum dla
w punkcie równym zero.

Dla wartości
wartość rzędnych wynosi zero. Krzywą charakteryzują dwa punkty przegięcia K1 i K2, leżące symetrycznie względem osi (). Ich położenie znajdujemy wstawiając wartości

do funkcji (1.51), a mianowicie

(1.52)

Prawdopodobieństwo tego, że błąd zawiera się między liczbami a i b, zaznaczonymi na osi , wyraża się powierzchnią pola ograniczonego osią od dołu, funkcją () od góry i rzędnymi = a i = b, w stosunku do całego pola ograniczonego osią i krzywą gęstości prawdopodobieństwa. Prawdopodobieństwo to dane jest całką

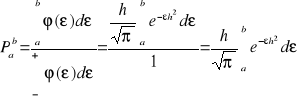
Prawdopodobieństwo tego, że błąd zawiera się między punktami przegięcia dla
wyraża się wzorem

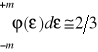
co oznacza, że prawdopodobieństwo popełnienia błędu mniejszego co do wartości bezwzględniej wartości błędu m wynosi w przybliżeniu 2/3. Wyrażenie to zapisane w postaci

(1.53)

należy zapamiętać z uwagi na wprowadzone później znaczenie błędu m. Tak więc dla podsumowania stwierdza się, że dla błędów przypadkowych wg (1.21) a = 0 oraz x = , gdzie oznacza błąd przypadkowy. Parametr zastąpiono przez błąd średni m. W takim razie zmienna standaryzowana t oznaczająca błąd przypadkowy wyrażony w jednostkach błędu średniego określana jest związkiem

(1.54)

Zatem wartość prawdopodobieństwa, że błąd przypadkowy pomiaru nie przekracza określonej wielkokrotności błędu średnigo, wyraża się

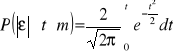
(1.55)

Prawostronna część wzoru (1.55) znana jest jako całka Laplace`a-Gaussa i bywa oznaczona w tablicach statystycznych symbolem (t). Fragmentem takiej tablicy jest tabela 1.2, przydatna do oceny prawdopodobieństwa występenia błędu o wielokrotności t.

Tabela 1.2

	(t)
0,5	0,3829
0,675	0,5000
1,0	0,6827
1,5	0,8664
2,0	0,9545
3,0	0,9973

1

20

---