Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie

Teoria maszyn i mechanizmów

Nr projektu:

5A

Tomasz Łata

Rok II, gr. 7A

Wydział IMiR

Założono następujące wymiary mechanizmu, oraz parametry jednego jego położenia.

Przyjęto wymiary mechanizmu oraz ograniczenia warunkujące jego prawidłową prace i działanie. Założono początkowe położenie mechanizmu, oraz prędkości i przyspieszenie członu napędzającego.

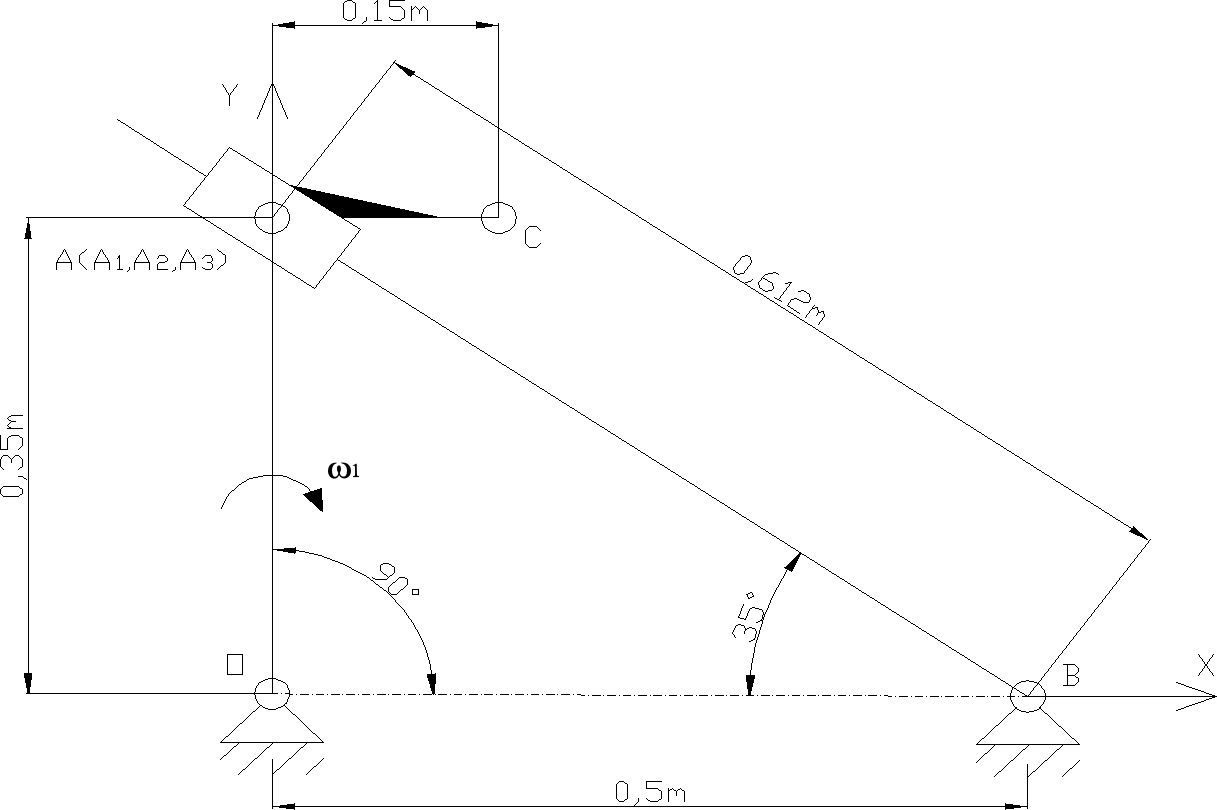
Przyjęto wymiary:

|OA|=0,35[m]

|AB|=0,612[m]

|AC|=0,15[m]

|OB|=0,5[m]

Kąty ustawienia członów dla jednego położenia

φ₁=90[°] φ₂=145[°]

Przyjęto prędkość i przyspieszenie członu napędzającego:

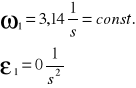
Wyznaczenie ruchliwości mechanizmu, podział na grupy strukturalne oraz klasyfikacja mechanizmu.

Podział na grupy strukturalne.

1. Podział mechanizmu

Analizowana grupa strukturalna jest klasy II

Ruchliwość mechanizmu wyznaczam ze wzoru:

w=3*n-p₄-2p₅

w- ruchliwość mechanizmu

n- liczba członów mechanizmu

p₄- para kinematyczna klasy czwartej

p₅- para kinematyczna klasy piątej

Określenie ruchliwości analizowanego mechanizmu

n= 3

p₄=0

p₅=4

Analiza kinematyczna mechanizmu.

Analiza kinematyczna wykonana jest metodą grafoanalityczną dla przedstawionego położenia mechanizmu.

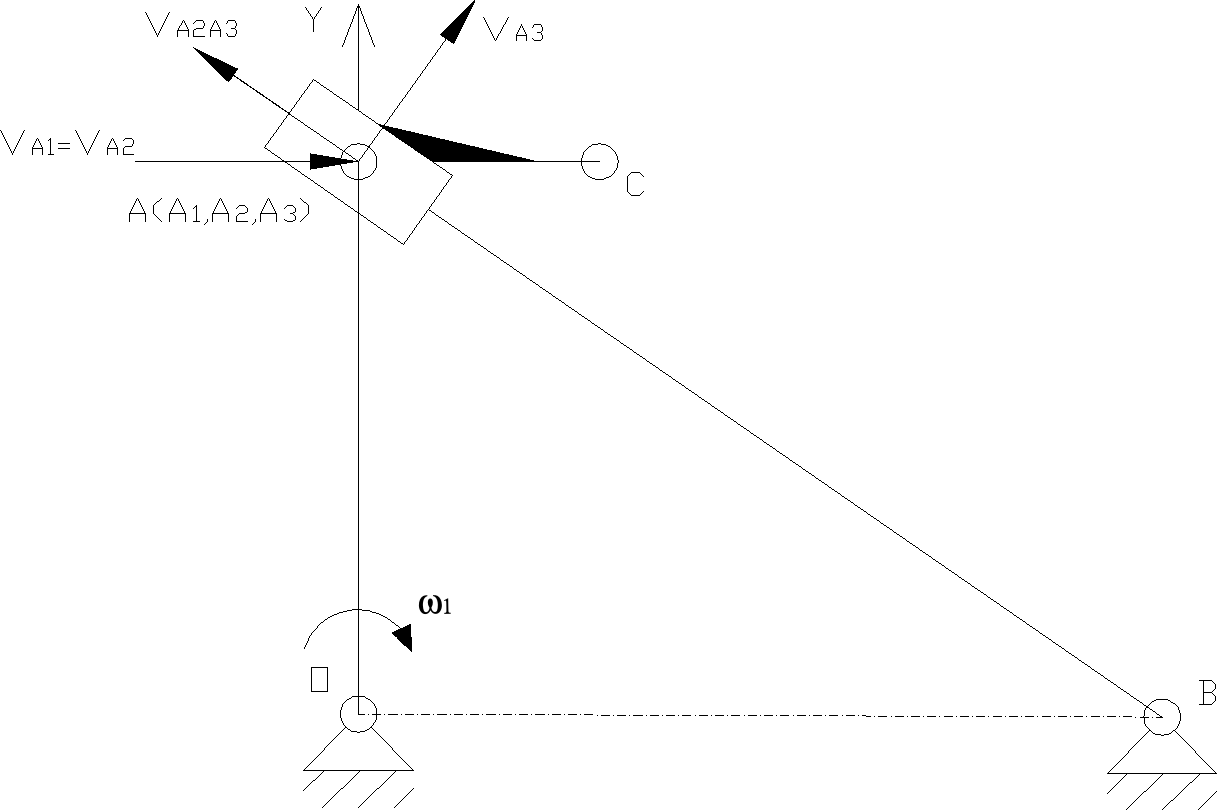
2. Schemat rozkładu prędkości

Grafoanalityczna analiza prędkości mechanizmu

Przyjęto prędkość członu napędzającego

ω₁=3,14[1/s]

Wyznaczenie prędkości V_A1

V_A1= ω₁·|0A1|=3,14·0,35=1,1

Wyznaczenie prędkości V_A2

V_A1= V_A2=1,1

Wyznaczenie prędkości V_A3

Wektor prędkości V_A2 jest jest prostopadły |0A|

Wektor prędkości V _A3A2 jest równoległy |AB|

Wektor prędkości V _A3 jest prostopadły |AB|

Wyznaczenie prędkości V_C

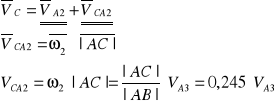
Wektor prędkości V _CA2 jest prostopadły |AC|

Prędkość (m₂) środka masy

Określenie podziałki rysunkowej dla planu prędkości:

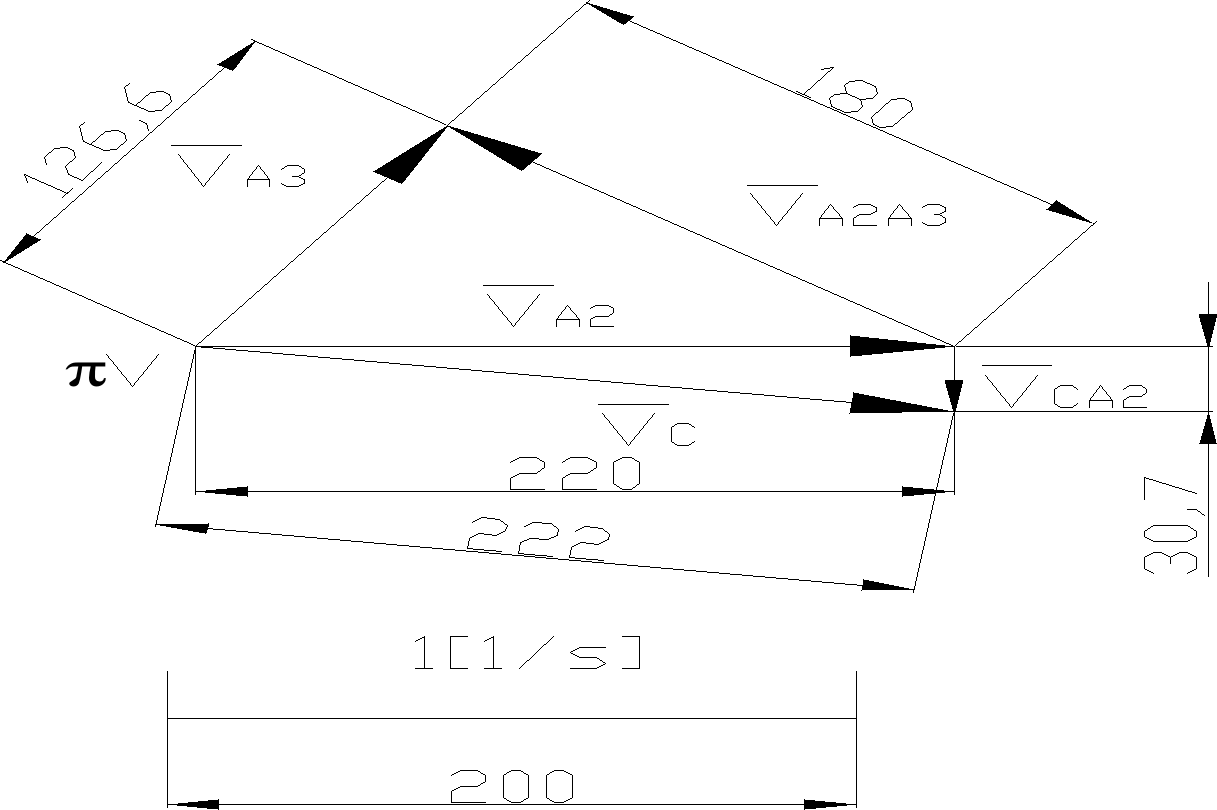
3. Plan prędkości

Z planu prędkości po uwzględnieniu skali odczytano następujące wartości

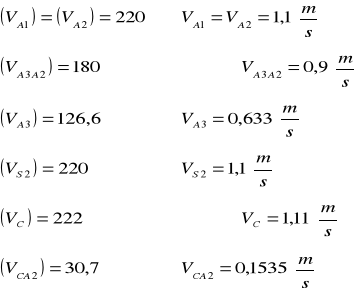
Wyznaczenie prędkości kątowej członu drugiego i trzeciego

Obliczenie przyśpieszeń mechanizmu metodą grafoanalityczną

Przyspieszenie kątowe członu napędzającego wynosi:

Przyspieszenie punktu A₁

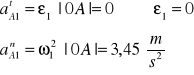
Wektor przyspieszenia a^t_A1 jest prostopadły |0A|

Wektor przyspieszenia aⁿ_A1 jest równoległy |0A|

Przyspieszenia punktu A₂

a_A1= a_A2=3,45

Przyspieszenie punktu A₃

gdzie

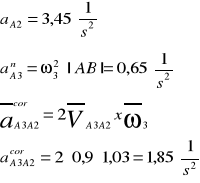
Wektor przyspieszenia a_A3ⁿ jest równoległy do |AB|

Wektor przyspieszenia a_A3^t jest prostopadły do |AB|

Wektor przyspieszenia a_A3A2^cor jest prostopadły do |AB|

Wektor przyspieszenia a_A3A2^t jest równoległy do |AB|

Wyznaczanie przyspieszenia punktu C

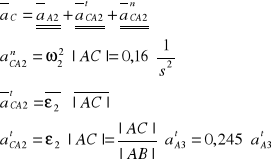
Wektor przyspieszenia a_CA2ⁿ jest równoległy do |AC|

Wektor przyspieszenia a _CA2^t jest prostopadły do |AC|

Wyznaczanie przyspieszenia punktu S₂

Przyjęcie podziałki rysunkowej dla planu przyśpieszeń:

4. Plan przyspieszeń

Wyniki

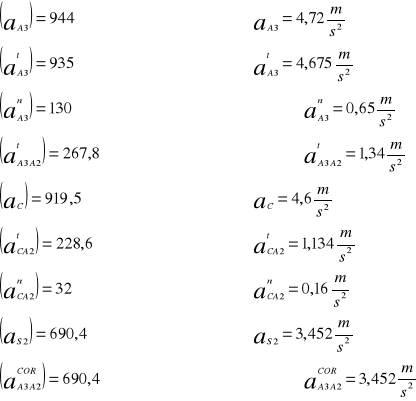
Wyznaczenie przyspieszenia kątowego członu trzeciego

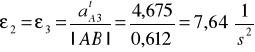
Analiza kinematyczna mechanizmu metodą analityczną.

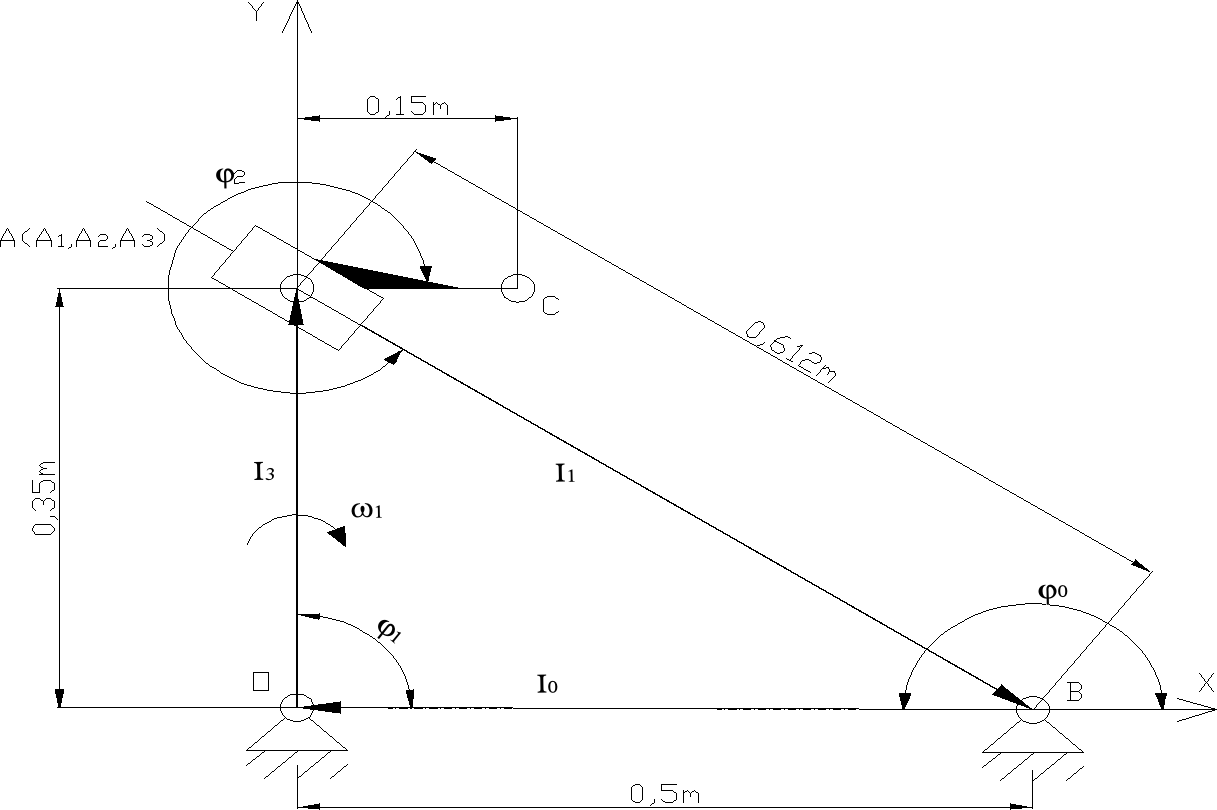
5. Schemat mechanizmu do analizy metodą analityczną

φ₁(t) określa ruch członu napędzającego

φ₂(t), l₃(t), są funkcjami zmiennymi w czasie

Poniższe funkcje są funkcjami stałymi i nie zależą od czasu, przyjmują zawsze stalą wartość:

l₁(t)=0,35[m]

l₀(t)=0,5[m] φ₀(t)=180 ^◦

Dla zadanego położenia mamy

φ₁(t₀=0)=90[°] ω₁(t₀=0)=3,14 [1/s] ε₁(t₀=0)=0 [1/s²]

Wyznaczenie ogólnych równań ruchu

Po przyjęciu układu współrzędnych i zrzutowaniu na osie otrzymujemy:

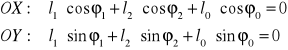
Obliczenie nieznanych prametrów

Nieznany parametr φ₂(t)

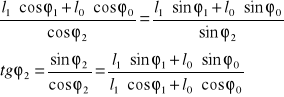
Po wstawieniu stałych parametrów otrzymujemy

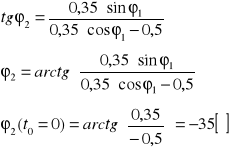
Dla jednego położenia mamy:

Nieznany parametr l₂(t)

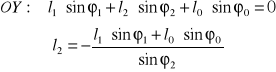
Po podstawieniu stałych parametrów mechanizmu oraz jednego położenia otrzymujemy

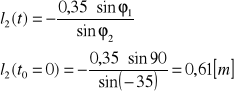
Analiza prędkości mechanizmu.

Różniczkując równania drogi po czasie otrzymamy zależność odpowiednich prędkości od czasu.

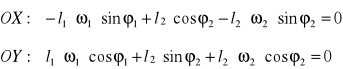
Nieznany parametr a₂(t)

Obracając układ o kąt φ₂(t) wyznaczy nieznany parametr z równania OX

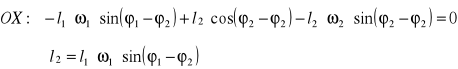
Dla jednego położenia mamy

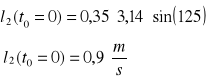
Nieznany parametr ω₂(t)

Obracając układ o kąt φ₂(t) wyznaczymy nieznany parametr z równania OY

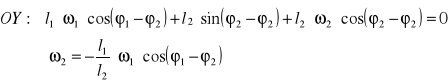
Dla jednego położenia mamy

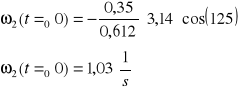
Określenie przyspieszeń mechanizmu

Różniczkując równania prędkości po czasie otrzymamy odpowiednie przyspieszenia.

Nieznany parametr a₂(t)

Nieznaną wartość przyspieszania wyznaczymy bezpośrednio z równania prędkości od czasu przez wyznaczenie pochodnej tego równania

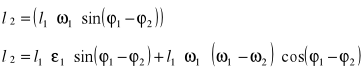
Dla jednego położenia mamy

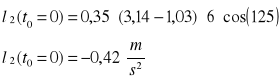
Nieznany parametr ε₂(t)

Nieznaną wartość przyspieszania wyznaczymy bezpośrednio z równania prędkości od czasu przez wyznaczenie pochodnej tego równania

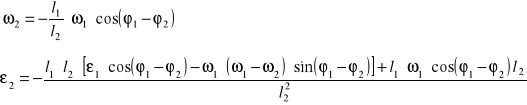
Dla jednego położenia mamy

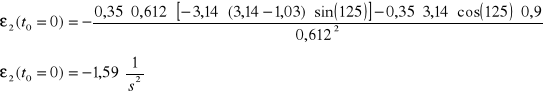
Analiza kinematyczna mechanizmu za pomocą programu SAM

Schemat mechanizmu zamodelowany w programie SAM

6. Schemat mechanizmu w SAMie

Wyniki analizy kinematycznej w programie

7. Wyniki analizy

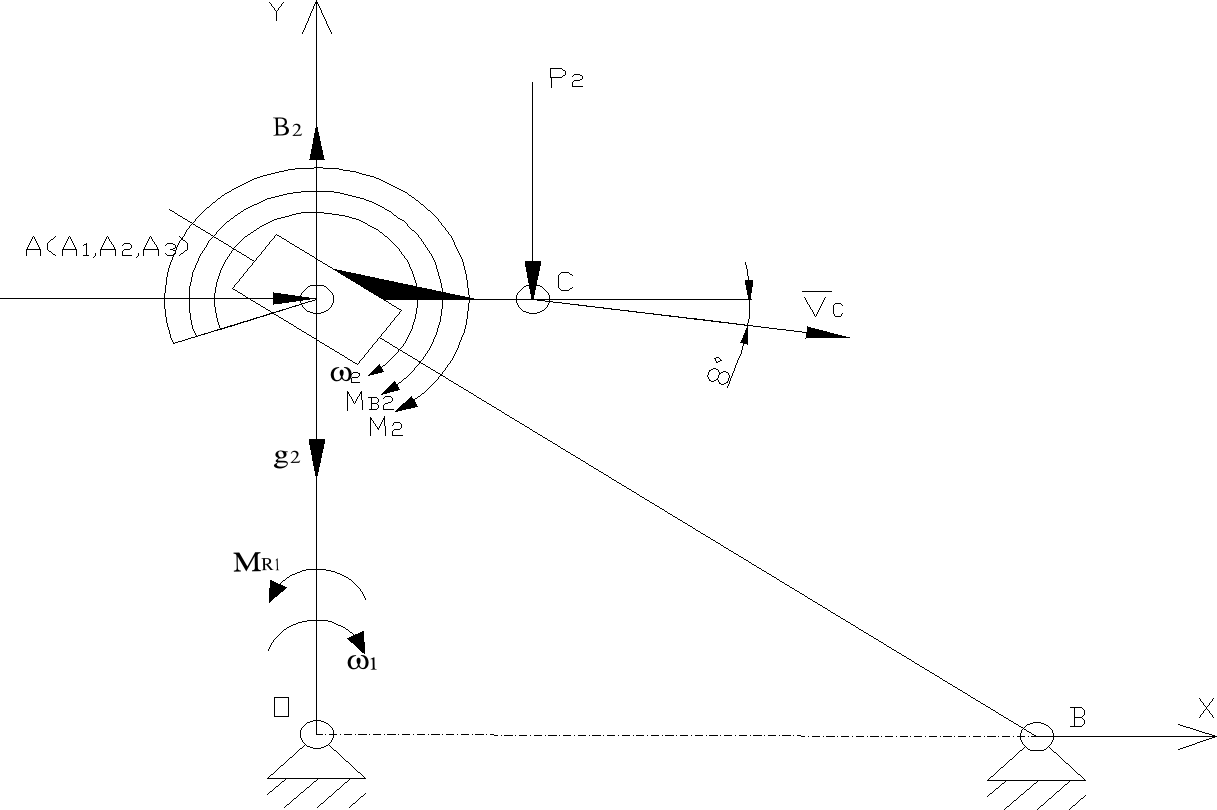
Analiza kinetostatyczna mechanizmu.

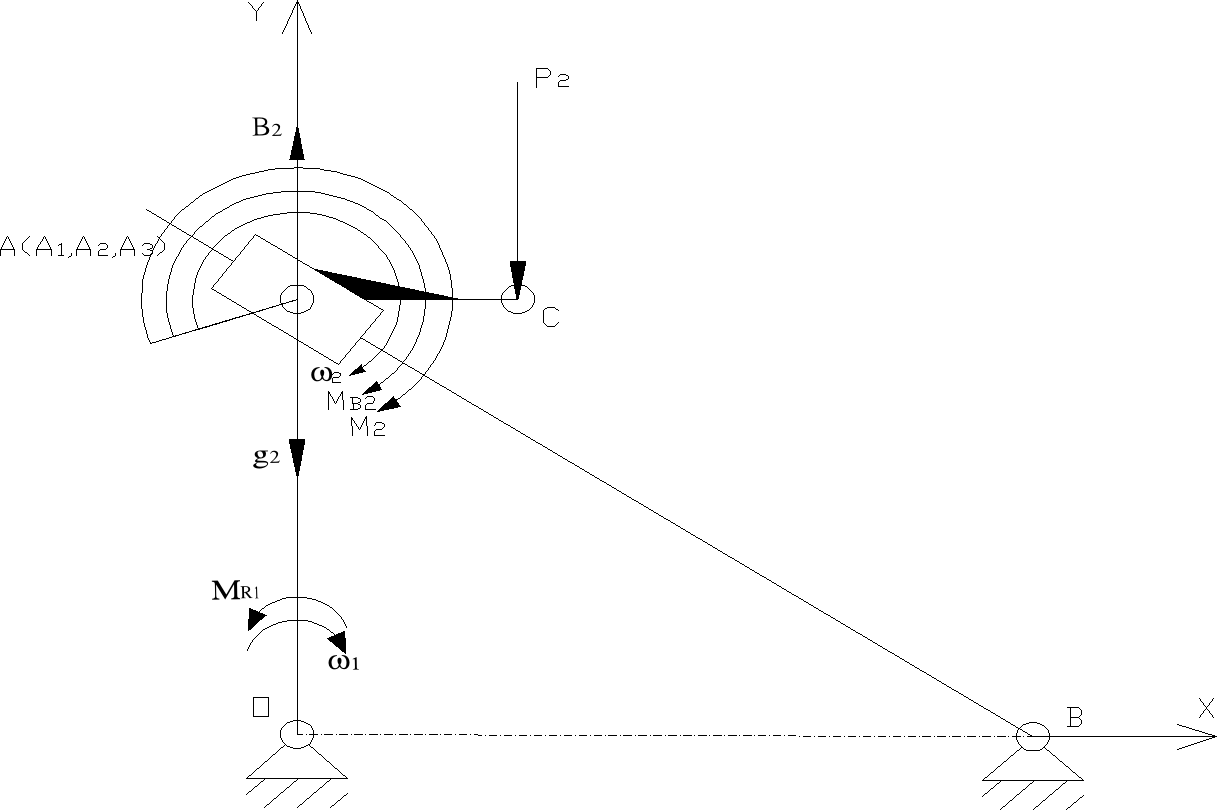
8. Mechanizm do analizy kienteostatycznej

Założenia analizy:

Przyjęto:

Wartości sił obciążających mechanizm:

M₂=10Nm

P₂=10N

Człon drugi mechanizmu posiada: masę m₂= 1 kg

Moment bezwładności J_S2

Mechanizm znajduje się w polu grawitacyjnym

Wyznaczenie sił bezwładności działających na mechanizm:

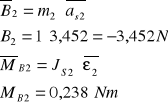
Wyznaczenie sił grawitacji działających na mechanizm:

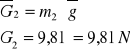
Odrzucenie członu napędzającego, oraz uwolnienie układu od więzów

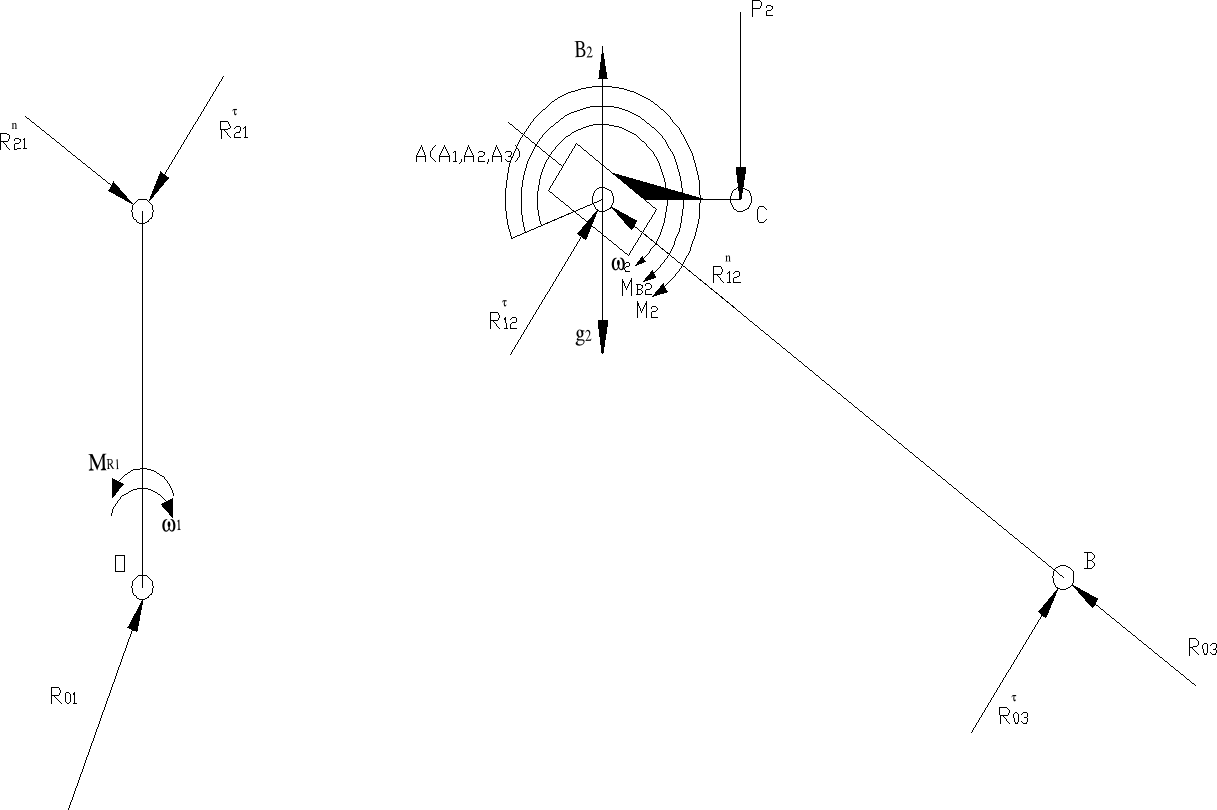
9. Uwolnienie układu od więzów (odrzucenie członu napędzającego)

Równanie wektorowe równowagi sił działających na grupę strukturalną

Dla grupy strukturalnej

Dla członu drugiego

Dla członu trzeciego

Wyznaczenie nieznanych reakcji z równania momentów i planu sił

Wyznaczenie nieznanej reakcji M₃₂ z równania momentów względem punktu B dla członu drugiego

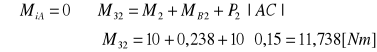
Wyznaczenie nieznanej reakcji R ^t₀₃ z równania momentów względem punktu A dla członu trzeciego

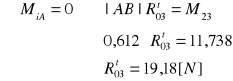
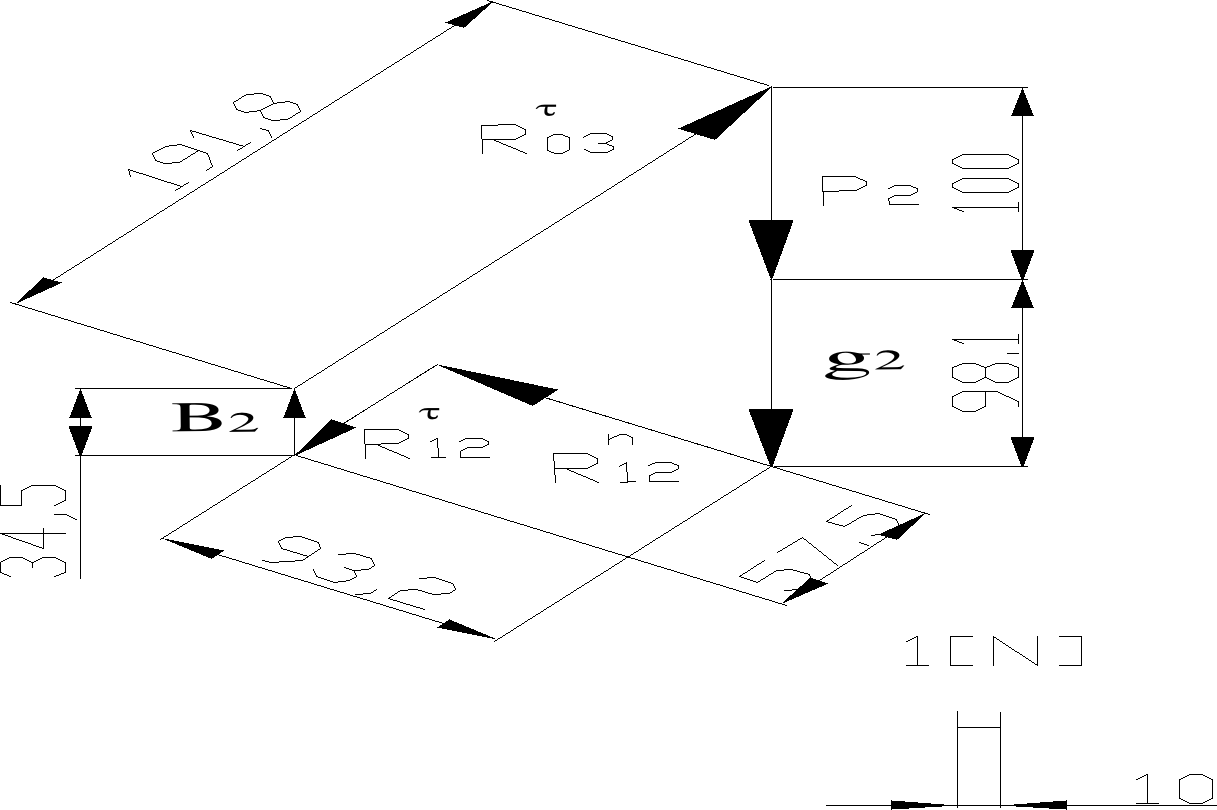
10. Plan sił

Na podstawie planu sił wyznaczono

1. Wyznaczenie siły równoważącej działającej na człon metoda mocy chwilowych

11. Mechanizm do analizy metodą mocy chwilowych

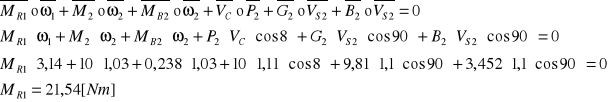
Siła równoważąca:

- 14 -

- 1 -

---