1Prawo Gaussa Elektryczność

Niech zamknięta powierzchnia obejmuje dwa ładunki Q₁ i Q₂. Całkowita liczba linii sił przecinająca powierzchnię zamkniętą wokół ładunków Q₁ i Q₂ jest równa

gdzie E₁ jest wytwarzane przez Q₁, a E₂ przez Q₂. Powołując się na wcześniejszy wynik otrzymujemy

φ_całk = (q₁/ε₀) + (q₂/ε₀) = (q₁ + q₂)/ε₀

Całkowita liczba linii sił jest równa całkowitemu ładunkowi podzielonemu przez ε₀. Podobnie można pokazać dla dowolnej liczby n ładunków.Otrzymujemy więc prawo Gaussa

,
, div - divergencja - odpowiednie różniczkowanie wektora po kierunkach x,y,z.

Magnetyzm

div
=0

2Indukcyjność

Gdy natężenie prądu przepływającego przez cewkę zmienia się to zmienia się też strumień przez każdy zwój tej cewki więc zgodnie z prawem indukcji Faradaya indukuje się SEM. Tę siłę elektromotoryczną nazywamy siłą elektromotoryczną samoindukcji.

Wielkość Nφ jest całkowitym strumieniem zawartym w obwodzie i nosi nazwę strumienia skojarzonego. Strumień skojarzony jest proporcjonalny do prądu płynącego przez cewkę.

Nφ = LI

L = Nφ/I

nazywana jest indukcyjnością.

Stąd

Jednostką L jest henr. 1 H = 1 Vs/A

Jako przykład obliczmy indukcyjność cewki o długości l₀ i N zwojach.

Strumień przez każdy zwój wynosi

φ = BS

gdzie B dla cewki wynosi

B = μ₀nI = μ₀I(N/l₀)

Zatem

Indukcyjność L otrzymujemy mnożąc strumień przez N/I

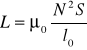
Zauważmy, że L zależy tylko od geometrii.

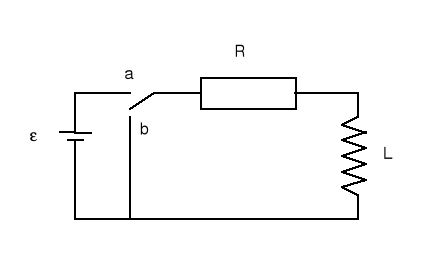
Układ RL

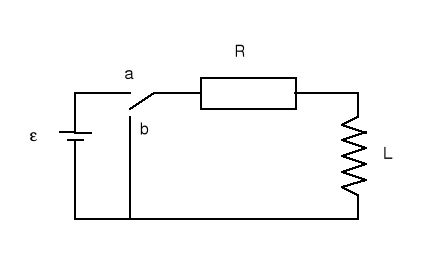
Gdyby nie było cewki prąd osiągnąłby natychmiast wartość ε/R. Dzięki cewce w obwodzie pojawia się dodatkowo SEM samoindukcji ε_L, która zgodnie z regułą Lenza przeciwdziała wzrostowi prądu (po włączeniu) co oznacza, że jej zwrot jest przeciwny do ε.

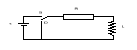
Z prawa Kirchoffa

Poszukujemy rozwiązania tego równania różniczkowego w postaci I(t).

Ma ono postać

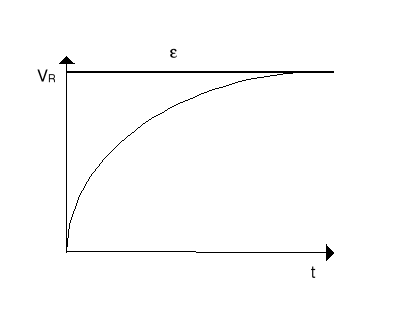
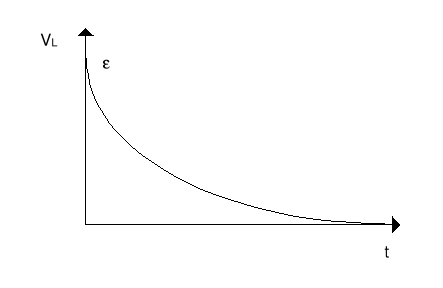
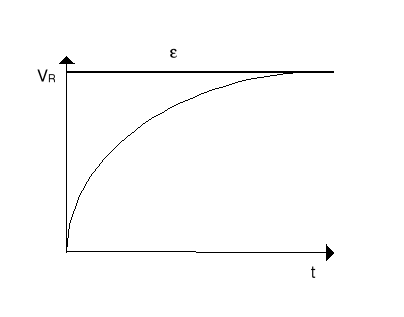
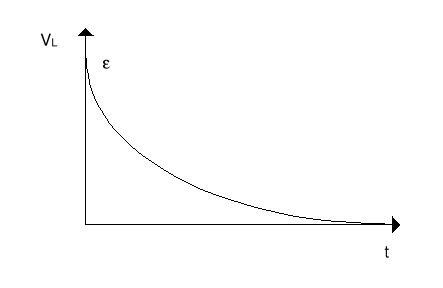
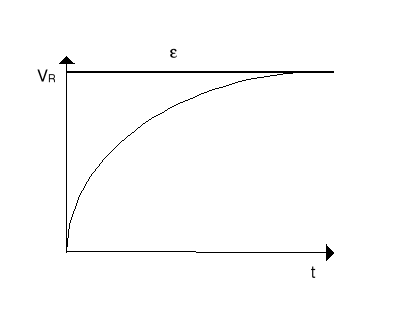
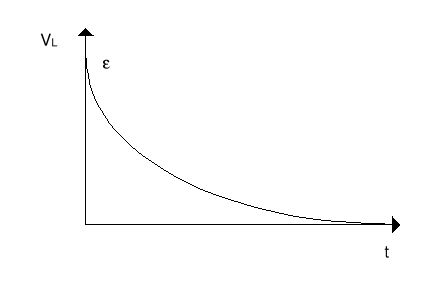
Sprawdzamy poprzez podstawienie do równania. Napięcie na oporniku i cewce pokazane jest na rysunkach poniżej.

Narastanie prądu w obwodzie jest opisane stałą czasową τ_L = L/R.

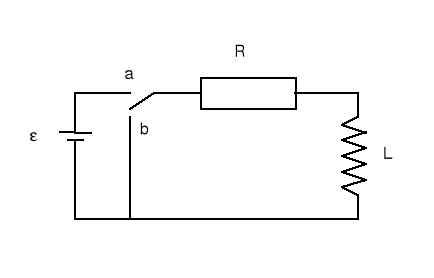
Jeżeli przełącznik ustawimy w pozycji (b) to wyłączmy źródło SEM i otrzymamy

3Dyfrakcja-zespół zjawisk związanych z falową naturą światła i obserwowanych podczas rozchodzenia się światła w ośrodku zawierającym silne niejednorodności optyczne. W wężym znaczeniu- zjawisko uginania światła na umieszczonych na jego drodze przeszkodach.

Dyfrakcja:

-Fresnela (w wiązce promieni zbieżnych)

-Fraunhofera (w wiązce promieni równoległych)

4Polaryzacja świetlna- wydzielenie światła o polaryzacji liniowej ze światła naturalnego lub częściowo spolaryzowanego W tym celu stosujemy specjalne przyrządy, zwane polaryzatorami. Działanie tych przyrządów, oparte jest na polaryzacji światła przy odpiciu i załamaniu na granicy dwóch ośrodków dielektrycznych, a także na zjawiskach dwójłomności i dichroizmu. Urządzenia te można również stosować jako analizatory (urządzenia określające rodzaj oraz stopień polaryzacji światła.)

Prawo Malusa

Dotyczy ono natężeń liniowo spolaryzowanego światła padającego na analizator i przez niego przepuszczonego

I = I_pcos²θ

1Prawo Gaussa Elektryczność

Niech zamknięta powierzchnia obejmuje dwa ładunki Q₁ i Q₂. Całkowita liczba linii sił przecinająca powierzchnię zamkniętą wokół ładunków Q₁ i Q₂ jest równa

gdzie E₁ jest wytwarzane przez Q₁, a E₂ przez Q₂. Powołując się na wcześniejszy wynik otrzymujemy

φ_całk = (q₁/ε₀) + (q₂/ε₀) = (q₁ + q₂)/ε₀

Całkowita liczba linii sił jest równa całkowitemu ładunkowi podzielonemu przez ε₀. Podobnie można pokazać dla dowolnej liczby n ładunków.Otrzymujemy więc prawo Gaussa

,
, div - divergencja - odpowiednie różniczkowanie wektora po kierunkach x,y,z.

Magnetyzm

div
=0

2Indukcyjność

Gdy natężenie prądu przepływającego przez cewkę zmienia się to zmienia się też strumień przez każdy zwój tej cewki więc zgodnie z prawem indukcji Faradaya indukuje się SEM. Tę siłę elektromotoryczną nazywamy siłą elektromotoryczną samoindukcji.

Wielkość Nφ jest całkowitym strumieniem zawartym w obwodzie i nosi nazwę strumienia skojarzonego. Strumień skojarzony jest proporcjonalny do prądu płynącego przez cewkę.

Nφ = LI

L = Nφ/I

nazywana jest indukcyjnością.

Stąd

Jednostką L jest henr. 1 H = 1 Vs/A

Jako przykład obliczmy indukcyjność cewki o długości l₀ i N zwojach.

Strumień przez każdy zwój wynosi

φ = BS

gdzie B dla cewki wynosi

B = μ₀nI = μ₀I(N/l₀)

Zatem

Indukcyjność L otrzymujemy mnożąc strumień przez N/I

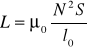
Zauważmy, że L zależy tylko od geometrii.

Układ RL

Gdyby nie było cewki prąd osiągnąłby natychmiast wartość ε/R. Dzięki cewce w obwodzie pojawia się dodatkowo SEM samoindukcji ε_L, która zgodnie z regułą Lenza przeciwdziała wzrostowi prądu (po włączeniu) co oznacza, że jej zwrot jest przeciwny do ε.

Z prawa Kirchoffa

Poszukujemy rozwiązania tego równania różniczkowego w postaci I(t).

Ma ono postać

Sprawdzamy poprzez podstawienie do równania. Napięcie na oporniku i cewce pokazane jest na rysunkach poniżej.

Narastanie prądu w obwodzie jest opisane stałą czasową τ_L = L/R.

Jeżeli przełącznik ustawimy w pozycji (b) to wyłączmy źródło SEM i otrzymamy

3Dyfrakcja-zespół zjawisk związanych z falową naturą światła i obserwowanych podczas rozchodzenia się światła w ośrodku zawierającym silne niejednorodności optyczne. W wężym znaczeniu- zjawisko uginania światła na umieszczonych na jego drodze przeszkodach.

Dyfrakcja:

-Fresnela (w wiązce promieni zbieżnych)

-Fraunhofera (w wiązce promieni równoległych)

4Polaryzacja świetlna- wydzielenie światła o polaryzacji liniowej ze światła naturalnego lub częściowo spolaryzowanego W tym celu stosujemy specjalne przyrządy, zwane polaryzatorami. Działanie tych przyrządów, oparte jest na polaryzacji światła przy odpiciu i załamaniu na granicy dwóch ośrodków dielektrycznych, a także na zjawiskach dwójłomności i dichroizmu. Urządzenia te można również stosować jako analizatory (urządzenia określające rodzaj oraz stopień polaryzacji światła.)

Prawo Malusa

Dotyczy ono natężeń liniowo spolaryzowanego światła padającego na analizator i przez niego przepuszczonego

I = I_pcos²θ

1Prawo Gaussa Elektryczność

Niech zamknięta powierzchnia obejmuje dwa ładunki Q₁ i Q₂. Całkowita liczba linii sił przecinająca powierzchnię zamkniętą wokół ładunków Q₁ i Q₂ jest równa

gdzie E₁ jest wytwarzane przez Q₁, a E₂ przez Q₂. Powołując się na wcześniejszy wynik otrzymujemy

φ_całk = (q₁/ε₀) + (q₂/ε₀) = (q₁ + q₂)/ε₀

Całkowita liczba linii sił jest równa całkowitemu ładunkowi podzielonemu przez ε₀. Podobnie można pokazać dla dowolnej liczby n ładunków.Otrzymujemy więc prawo Gaussa

,
, div - divergencja - odpowiednie różniczkowanie wektora po kierunkach x,y,z.

Magnetyzm

div
=0

2Indukcyjność

Gdy natężenie prądu przepływającego przez cewkę zmienia się to zmienia się też strumień przez każdy zwój tej cewki więc zgodnie z prawem indukcji Faradaya indukuje się SEM. Tę siłę elektromotoryczną nazywamy siłą elektromotoryczną samoindukcji.

Wielkość Nφ jest całkowitym strumieniem zawartym w obwodzie i nosi nazwę strumienia skojarzonego. Strumień skojarzony jest proporcjonalny do prądu płynącego przez cewkę.

Nφ = LI

L = Nφ/I

nazywana jest indukcyjnością.

Stąd

Jednostką L jest henr. 1 H = 1 Vs/A

Jako przykład obliczmy indukcyjność cewki o długości l₀ i N zwojach.

Strumień przez każdy zwój wynosi

φ = BS

gdzie B dla cewki wynosi

B = μ₀nI = μ₀I(N/l₀)

Zatem

Indukcyjność L otrzymujemy mnożąc strumień przez N/I

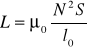
Zauważmy, że L zależy tylko od geometrii.

Układ RL

Gdyby nie było cewki prąd osiągnąłby natychmiast wartość ε/R. Dzięki cewce w obwodzie pojawia się dodatkowo SEM samoindukcji ε_L, która zgodnie z regułą Lenza przeciwdziała wzrostowi prądu (po włączeniu) co oznacza, że jej zwrot jest przeciwny do ε.

Z prawa Kirchoffa

Poszukujemy rozwiązania tego równania różniczkowego w postaci I(t).

Ma ono postać

Sprawdzamy poprzez podstawienie do równania. Napięcie na oporniku i cewce pokazane jest na rysunkach poniżej.

Narastanie prądu w obwodzie jest opisane stałą czasową τ_L = L/R.

Jeżeli przełącznik ustawimy w pozycji (b) to wyłączmy źródło SEM i otrzymamy

3Dyfrakcja-zespół zjawisk związanych z falową naturą światła i obserwowanych podczas rozchodzenia się światła w ośrodku zawierającym silne niejednorodności optyczne. W wężym znaczeniu- zjawisko uginania światła na umieszczonych na jego drodze przeszkodach.

Dyfrakcja:

-Fresnela (w wiązce promieni zbieżnych)

-Fraunhofera (w wiązce promieni równoległych)

4Polaryzacja świetlna- wydzielenie światła o polaryzacji liniowej ze światła naturalnego lub częściowo spolaryzowanego W tym celu stosujemy specjalne przyrządy, zwane polaryzatorami. Działanie tych przyrządów, oparte jest na polaryzacji światła przy odpiciu i załamaniu na granicy dwóch ośrodków dielektrycznych, a także na zjawiskach dwójłomności i dichroizmu. Urządzenia te można również stosować jako analizatory (urządzenia określające rodzaj oraz stopień polaryzacji światła.)

Prawo Malusa

Dotyczy ono natężeń liniowo spolaryzowanego światła padającego na analizator i przez niego przepuszczonego

I = I_pcos²θ

---