Instrukcja do zajęć laboratoryjnych nr 2. Katedra Podstaw Konstrukcji Maszyn
Metody Numeryczne
Temat: Interpolacja (2) - przybliżanie funkcji zadanej analitycznie
(wzór Czebyszewa, interpolacja geometryczna )
Zadanie do wykonania
a) Wielomiany Czebyszewa
Celem ćwiczenia jest wyznaczenie wielomianu interpolacyjnego dla zadanego zbioru wartości xi i = 0,1, ... , n, argumentów funkcji interpolowanej, które mieszczą w przedziale xi ∈ [-1, 1. Bazę Czebyszewa T0(x), T1(x), ... Tn(x) stanowi zbiór wielomianów określonych wzorem rekurencyjnym:
Tk+1(x) = 2xTk(x), ... Tk-1(x), To (x) = 1, T1(x) = x. (1)
Współczynniki wzoru interpolacyjnego Czebyszewa wynikają z układu równań:
![]()
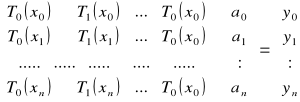
(2)
Przykładowy wielomian interpolacyjny Czebyszewa stopnia drugiego:
W(x) = a0T0(x) + a1T1(x) + a2T2(x) (3)
czyli
W(x) = a0 + a1x + a2(2x2 - 1) (4)
b) interpolacja trygonometryczna
Jako bazę interpolacji przyjmiemy w tej metodzie zbiór funkcji trygonometrycznych:
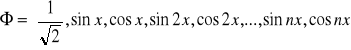
(5)
Wielomianem interpolacyjnym będzie suma w postaci:
![]()
(6)
zawierająca 2n + 1 nieznanych parametrów. Najbardziej istotny w praktyce jest przypadek interpolacji funkcji określonej na zbiorze równoodległych węzłów xi∈[0,2π] dobranych następująco:
![]()
, i = 0, 1, ..., 2n (7)
Założenia
Przed przystąpieniem do rozwiązywania zadania prowadzący zajęcia zobowiązany jest przedstawić każdej sekcji zbiór danych wejściowych. Dane te należy zapisać w postaci macierzowej.
Podczas wykonywania zadania nie można korzystać z funkcji wewnętrznych programu MATLAB związanych z działaniami na macierzach. Wyjątek stanowi funkcja „zeros ()” , „size ()”, „length()” oraz „plot ()”.
Zadania do wykonania
Aby otrzymać wielomian interpolacyjny Czebyszewa, należy:
zdefiniować funkcję argumentową Czebyszew (X,Y), której argumentami będą podane przez prowadzącego dane wejściowe (patrz p.2), w funkcji należy m.in.:
zbudować tabele wielomianów składowych,
wyznaczyć wielomian interpolacyjny stopnia 2,
stosując funkcję plot przedstawić na jednym wykresie węzły interpolacji oraz graficzną reprezentacje otrzymanego wielomianu,
w celu przedstawienia powyższych danych na jednym wykresie zastosować flagę hold z parametrem on,
Aby otrzymać wielomian interpolacyjny wg interpolacji trygonometrycznej, należy:
należy zdefiniować funkcję argumentową trygonom (X,Y), której argumentami będą podane przez prowadzącego dane wejściowe,
ustalić stopień wielomianu interpolacyjnego na 4,
zbudować macierz X zawierającą wartości funkcji trygonometrycznych wg wzoru (5),
transponować macierz X ,
zbudować macierz X-1=2/(2n+1)*XT,
zbudować macierz będącą iloczynem X*Y (lub X*YT - w zależności od postaci utworzonej macierzy Y wartości funkcji f(X)),
obliczyć wartości współczynników wzoru interpolacyjnego,
stosując funkcję plot przedstawić na jednym wykresie węzły interpolacji oraz graficzną reprezentacje otrzymanego wielomianu,
w celu przedstawienia powyższych danych na jednym wykresie zastosować flagę hold z parametrem on,
Literatura
[1] Majchrzak E., Mochnacki B., „Metody numeryczne. Podstawy teoretyczne, aspekty praktycne i algorytmy", wydawnictwo Politechniki Śląskiej, Gliwice 1994 (i dalsze).
[2] Cegieła R., Zalewski A., „Matlab - obliczenia numeryczne i ich zastosowania”, Wydawnictwo Nakom, Poznań 1996.
[3] Sedgewick R., „Algorithms”, Addison-Wesley, USA 1983.
Opracował: Marek WYLEŻOŁ 99-02-24
Wyszukiwarka
Podobne podstrony:
mn eliminacja gaussa, Politechnika Śląska ZiIP i inne, Mechanika
Wprowadzenie do Matlaba w97, Politechnika Śląska ZiIP i inne, Mechanika
Interpretacja geometryczna, Politechnika Śląska ZiIP i inne, Matematyka
ruch-plaski-wahadlo2, Politechnika Śląska ZiIP i inne, Mechanika
ruch-plaski-wahadlo3, Politechnika Śląska ZiIP i inne, Mechanika
ruch prostoliniowy, Politechnika Śląska ZiIP i inne, Mechanika
wzory Finanase przedsiebiorstw, Politechnika Śląska ZiIP i inne, Finanse
Testy 5 ekonomika podatkowa, Politechnika Śląska ZiIP i inne, Ekonomika podatkowa
FINANSE[1][1], Politechnika Śląska ZiIP i inne, Finanse
finanse(2), Politechnika Śląska ZiIP i inne, Finanse
więcej podobnych podstron