Interpretacja geometryczna:
Całka oznaczona ma prostą interpretację geometryczną w przypadku funkcji nieujemnej, tzn. gdy f(x)Ⴓ0 dla x სa, bჱ.
Suma Sn jest sumą pól n prostokątów zakreskowanych na rysunku 1 i jednocześnie przybliżoną wartością pola |D| obszaru D ograniczonego wykresem funkcji f(x), osią OX oraz prostymi x = a i x = b.
Przy podziale przedziału სa, bჱ na coraz mniejsze podprzedziały, każdy prostokąt jest coraz węższy i suma Sn jest coraz lepszym przybliżeniem pola obszaru D.
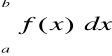
Zatem całka oznaczona jest więc to pole figury ograniczonej
przez krzywą y = f(x), oś OX oraz proste x = a i x = b.
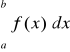
Wyszukiwarka
Podobne podstrony:
mn interpolacja2 lab3, Politechnika Śląska ZiIP i inne, Mechanika
wzory Finanase przedsiebiorstw, Politechnika Śląska ZiIP i inne, Finanse
Testy 5 ekonomika podatkowa, Politechnika Śląska ZiIP i inne, Ekonomika podatkowa
FINANSE[1][1], Politechnika Śląska ZiIP i inne, Finanse
finanse(2), Politechnika Śląska ZiIP i inne, Finanse
Finanse publiczne i rynki finansowe, Politechnika Śląska ZiIP i inne, Finanse
finanse lokalne, Politechnika Śląska ZiIP i inne, Finanse
FINANSE ciga, Politechnika Śląska ZiIP i inne, Finanse
finanse1, Politechnika Śląska ZiIP i inne, Finanse
Wprowadzenie do Matlaba w97, Politechnika Śląska ZiIP i inne, Mechanika
mn eliminacja gaussa, Politechnika Śląska ZiIP i inne, Mechanika
ruch-plaski-wahadlo2, Politechnika Śląska ZiIP i inne, Mechanika
ruch-plaski-wahadlo3, Politechnika Śląska ZiIP i inne, Mechanika
FINANSE pytania, Politechnika Śląska ZiIP i inne, Finanse
więcej podobnych podstron