Próba jest taką częścią populacji, że rozkład wartości cechy w próbie reprezentatywnej jest zbliżony do rozkładu wartości cechy w populacji.

Próba jest reprezentatywna, jeżeli struktura jednostkowa statystyki w próbie odpowiada strukturze populacji.

Rozkładem populacji generalnej nazywamy rozkład badanej cechy populacji.

Próbą prostą o liczebności n-elementowej wylosowaną ze skończonej lub nieskończonej populacji nazywa się próbę losową, której wyniki są niezależnymi zmiennymi losowymi o jednakowych rozkładach identycznych z rozkładem populacji.

Twierdzenie Gliwienki

Niech F(x) oznacza dystrybuantę teoretyczne natomiast Gn(x) dystrybuantę wart. Cechy w n-elementowej próbie. Jeżeli wyniki losowania elementów do próby są zdarzeniami niezależnymi wówczas:

Próba prosta to n-wymairowa zmienna losowa (wektor losowy) X=(X₁,X₂,...,Xn) taka, że:

1. X₁,...,Xn są niezależnymi zmiennymi losowymi

2. Każda zmienna losowa Xi (i-ty wynik w próbce) ma rozkład identyczny z rozkładem populacji.

Realizacją próby X nazwiemy wektor x realizacji zmiennej losowej X₁,...,Xn tworzących próbę:

• Wszystkie możliwe realizacje wektora x=(x₁,...,xn) próby stanowią zbiór X punktów w n-wymiarowej przestrzeni Rⁿ

• Wektor liczb stanowiących jedną realizację jest punktem w przestrzeni prób

Zakładamy, że przestrzeń prób X jest mierzalna:

- można zbudować z jej elementów ciało zd. A

- można określić na nim miarę parabilistyczną P charakteryzującą rozkład prób.

Z przestrzenią prób wiążemy przestrzeń propabilistyczną (X,A,P), na której możemy określić zmienne losowe zwane statystykami.

ROZKŁAD GAMMA

dla x>0, b,p>0

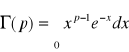
Wartości tej całki są stablicowane. Wiadimo, że:

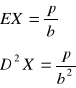
Dla rozkładu Gamma zachodzi tw. o addytywności - suma niezależnych zmiennych losowych o rozkładach Gamma ma rozkład Gamma

Dla szczególnych wartości parametrów:

1)
oraz
mamy: rozkład wykładniczy

>0, x>0

2)
oraz
(k
N) mamy: rozkład Chi²

ROZKŁAD CHI²

Niech Z1,...,Zn ~ N(0,1) i są niezależne, wówczas każda zmienna losowa będąca sumą ich kwadratów ma rozkład χ² o n-stopniach swobody.

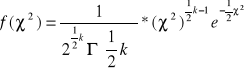
dla χ² > 0

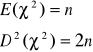
rozkład prawostronnie symetryczny

Siła asymetrii f. gęstości maleje wraz ze wzrostem stopni swobody.

Twierdzenie

Rozkład χ² przy dużej liczbie swobody (n→∞) jest zbieżny do rozkładu normalnego:

gdy n→∞

Jeżeli U jest wektorem o n-wymiarowym rozkładzie normalnym N(O,I) to forma kwadratowa U^TAU ma rozkład χ² o liczbie stopni swobody równej rzędowi r(A).

Dla rozkładu χ² zachodzi tw. o addytywności.

ROZKŁAD t-STUDENTA

Zmienną losową o rozkładzie t-Studenta o n stopniach swobody definiujemy jako:

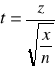
gdzie Z-N(0,1) oraz X²- χ² o n-stopniach swobody. Zmienne Z i X są niezależne:

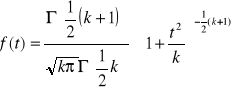
Rozkład symetryczny: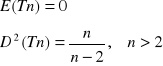

Dla szczególnej wartości parametru n=1 mamy: rozkład CAUCHEGO

- nie istnieją momenty skończone tego rozkładu!!!

ROZKŁAD F.SNEDECORA

Zmienne losowe o rozkładzie F.Snedecora o n i p stopniach swobody to:

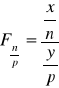
gdzie: X,Y χ² o n i p stopniach swobody

Zmienne X i Y są niezależne.

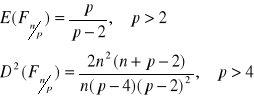
rozkład prawostronnie asymetryczny

Jeżeli zmienna t ma rozkład Studenta z k-stopniami swobody to zmienna losowa F=t², ma rozkład F.Snedecora o n=1 i p=k stopniach swobody.

Jeżeli p→∞ to zmienna losowa nF ma graniczny rozkład χ² o n-stopniach swobody.

Z definicji rozkładu F.Snedecora wiemy, że zmienna:
ma rozkład F.Snedecora o p i n stopniach swobody.

Twierdzenie graniczne np. Lindberga - Levy'ego

Jeżeli dana ciągła zmienna losowa X ma rozkład o funkcji gęstości f(x) i jeżeli g(x) jest pewną monotoniczną i różniczkowalną funkcją, a h jest funkcją do niej odwrotną, to zmienna losowa Y=g(x) ma rozkład określony funkcją:

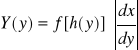
, gdzie x=h(y)

ESTYMACJA

Niech X=(X₁,...,Xn) będzie n-elementową próbą prostą wylosowaną z populacji o rozkładzie F(x;Θ). Niech Tn = g(x) będzie dowolną statystyką. Estymatorem nazwiemy taką statystykę, której rozkład zależy od szacowanego parametru:

Tn(X₁,X₂,...,Xn; Θ)

Ocena parametru Θ to wartość estymatora Tn dla próby statystycznej x₁,...,x_n

Tn(x₁,...,x_n)=t_n

Błąd szacunku - zmienna losowa:

Tn(X₁,X₂,...,X_n; Θ)- Θ =...

Standardowy błąd szacunku:

Wynik estymacji:

tn ± D(Tn)

Własności estymatorów gwarantujące małe błędy szacunku:

- nieobciążoność

- efektywność

- zgodność

- dostateczność

Estymator nieobciążony jest najefektywniejszy, jeżeli wśród wszystkich estymatorów nieobciążonych tego parametru ma najmniejszą wariancję.

Odwrotność wariancji estymatora nazywa się jego precyzją.

Błąd średniokwadratowy estymatora

MSE(Tn) = D²(Tn) + [B(Tn)]²

MSE(Tn) = E(Tn - Ө)² - błąd średniokwadratowy estymatora (ang. Mean Square Error)

jest miara estymacji i informuje, o ile przeciętnie wartości estymatora odchylają się od rzeczywistej wartości estymatora.

Czym mniejszy MSE (pierwiastek z MSE) tym większa dokładność.

D²(Tn) = E(Tn - E(Tn))² - wariancja estymatora (
- średni błąd szacunku estymatora)

D(Tn) jest miarą precyzji estymacji i informuje, o ile przeciętnie wartości estymatora odchylają się od wartości oczekiwanej estymatora.

Czym mniejsza wariancja (średni błąd szacunku) tym większa precyzja.

B(Tn) = E(Tn) - Ө - obciążenie estymatora

Gdy obciążenie estymatora wynosi zero to estymator jest nieobciążony, czyli oszacowania nie są obciążone błędem systematycznym.

UWAGA!!!

Jeśli estymator Tn jest nieobciążony (czyli gdy E(Tn) = Y) wówczas MSE(tn) = D²(Tn) i przy interpretacji błędu szacunku D(tn) można skorzystać z interpretacji pierwiastka błędu średniokwadratowego
.

Własności estymatorów

Estymator nazywa się nieobciążonym, jeśli E(Tn) = Ө (czyli B(Tn) = 0).

Estymator nazywa się asymptotycznie nieobciążonym, jeśli

Estymator nazywa się zgodnym, jeśli
przy każdej dowolnie małej wartości є.

• Twierdzenie: Jeśli
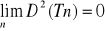
  i estymator jest nieobciążony lub asymptotycznie nieobciążony to estymator jest zgodny.

Nieobciążony estymator Tn* nazywamy efektywnym jeśli ma najmniejszą wariancję ze wszystkich estymatorów należących do klasy estymatorów nieobciążonych.

Wskaźnik efektywności estymatora Tn (gdzie Tn* jest estymatorem efektywnym):

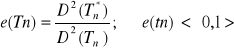
Twierdzenie. Nierówność Rao-Cramera.

Jeżeli Tn jest estymatorem nieobciążonym parametru Θ rozkładu populacji spełniającego warunek regularności (różniczkowalność względem Θ przynajmniej 2 rzędu) to jego wariancja D²(Tn) spełnia nierówność:

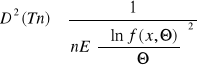
dla rozkładu ciągłego populacji z funkcją gęstości f(x,Θ) lub

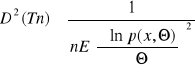
dla skokowego rozkładu populacji z funkcją prawdopodobieństwa p(x, Θ)

Prawa strona określa wariancję estymatora najefektywniejszego (kres dolny zbioru).

Estymator Tn parametru Θ nazywa się dostatecznym jeżeli można ze względu na niego dokonać faktoryzacji (rozłożenia na iloczyn) łącznej funkcji gęstości f(x) wektora wyników próby x=(x₁,…,x_n).

f(x, Θ) = h(Tn, Θ) * g(x, Tn)

gdzie g(x, Tn) jest funkcją niezależną od parametru Θ.

Najczęściej łączną funkcję gęstości dla prób prostych zapisujemy jako:

wówczas dla estymatora dostatecznego zachodzi:

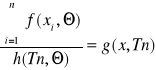
Funkcja informacyjna (Fishera) rozkładu zmiennej losowej Y określonej funkcją gęstości Φ(y) nazywamy wyrażenie:

Równość faktoryzacyjną po zlogarytmizowaniu można zapisać:

różniczkując po Θ mamy:

Estymator dosteczny skupia wszystkie informacje o pararametrze Θ zawarte w próbie losowej.

Twierdzenie.

Warunkiem koniecznym na to, by estymator nieobciążony Tn parametru Θ był estymatorem najefektywniejszym jest, by był to estymator dostateczny parametru Θ.

Warunkiem dostatecznym jest zachodzenie równości:

gdzie, c nie zależy od Θ.

Metody estymacji:

1. Metoda momentów

2. Metoda największej wiarygodności

3. Metoda najmniejszych kwadratów

METODA MOMENTÓW - dla dużych prób!

Estymator parametru Θ będącego pewnym momentem rzędu r populacji jest odpowiednim momentem z próby.

Estymatory uzyskiwane tą metodą są: zgodne, obciążone, nieefektywne.

METODA NAJWIĘKSZEJ WIARYGODNOŚCI (MNW)

Pozwala na znalezienie parametrów w takich rozkładach populacji, których postać funkcyjna jest znana.

Wiarygodnością (funkcją wiarygodności) n-elementowej próby prostej nazywamy wyrażenie postaci:

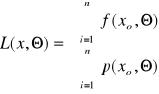
f(xi, Θ) - jest funkcją gęstości

p(xi, Θ) - jest funkcją prawdopodobieństwa

Θ - jest pojedynczym parametrem lub wektorem parametrów

Estymatorem najwiarygodniejszym nazywamy taki estymator Tn= Θ parametru Θ, że jego wartości maksymalizuje wiarygodność próby.

W praktyce znajdujemy ekstremum funkcji ln α (ekstremum jest w tym samym punkcie, co dla α, a różniczkowanie jest łatwiejsze)

- dla próby prostej α, to iloczyn ln α jest sumą.

Twierdzenie

Jeżeli istnieje najefektywniejszy oraz dostateczny estymator parametru Θ, to można je otrzymać MNW.

Twierdzenie.

Jeżeli Tn jest najwiarygodniejszym estymatorem parametru Θ w ciągłym rozkładzie populacji, to estymator ten (dla dużych prób) ma rozkład asymptotycznie normalny.

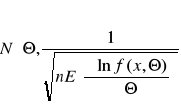
Twierdzenie.

Jeżeli
jest najwiarygodniejszym estymatorem parametru Θ, a Q=g(Θ) jest innym parametrem, będącym monotonicznym przekształceniem parametru Θ, to najwiarygodniejszym jego estymatorem jest

Własności estymatorów uzyskiwanych MNW:

- asymptotyczna nieobciążoność

- zgodność

- asymptotyczne efektywność

- niezmienność względem monotonicznych przekształceń

METODA NAJMNIEJSZYCH KWADRATÓW

Stosowana do estymacji parametrów funkcji wyrażających różne zależności pomiędzy zmiennymi losowymi, których łączne obserwacje stanowią wyniki próby z wielowymiarowej populacji.

Metoda ta polega na takim dobraniu szacowanych parametrów, że suma kwadratów odchyleń empirycznych wartości danej funkcji od jej szacowanych wartości była minimalna.

Niech g(x, Θ) będzie pewną funkcją w wielowymiarowym rozkładzie wektora losowego, którego obserwacje (xi,yi) dla i=1,2,…,n elementową próbę prostą.

Estymatorem otrzymanym MNK nazywamy taki estymator wektora Θ funkcji g, którego wartości, czyli wektor:

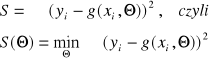
Należy rozwiązać układ równań

układ równań minimalnych w MNK.

Najczęściej MNK stosowana jest do szacowania parametrów takiej funkcji g, że jest ona funkcją regresji Y względem wektora zmiennych X w wielowymiarowym rozkładzie (Y,X).

Do liniowej funkcji g estymatory uzyskane MNK są:

zgodne, nieobciążone, najefektywniejsze (w klasie estymatorów liniowych).

• Im mniejsza próba tym mniejsze obciążenie estymatora.

• Im mniejszy poziom ufności tym mniejsza długość przedziału ufności

• Im większa próba tym mniejsza długość przedziału ufności.

• Poziom istotności to prawdopodobieństwo popełnienia błędu pierwszego rodzaju polegającego na odrzuceniu prawdziwej hipotezy Ho.

Hipoteza Ho Decyzja	Prawdziwa	Fałszywa
Przyjąć	Decyzja prawidłowa	Błąd 2 rodzaju (prawd. Β)
Odrzucić	Błąd 1 rodzaju (prawd. Α)	Decyzja prawidłowa

• Obszar krytyczny zależy od:

• Sformułowanej H₁

• Rodzaju statystyki testowej

• Poziomu istotności
  

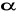
• Obserwowany poziom istotności (p) dla ustalonego testu statystycznego jest to prawdopodobieństwo odpowiadające obserwowanej wartości testu wyznaczonej dla próby statystycznej

p <


Jeżeli poziom istotności mamy mniejszy od urojonego poziomu istotności testu (np. 0,05) wówczas odrzucamy H₀

• Jeżeli wartość statystyki testowej wpada do obszaru krytycznego to odrzucamy hipotezę Ho na rzecz hipotezy H₁. Wówczas z prawdopodobieństwem (1-α) można twierdzić, że prawdziwa jest hipoteza H₁.

Jeżeli wartość statystyki testowej nie wpada do obszaru krytycznego to niema podstaw do odrzucenia hipotezy H₀. Wówczas można przyjąć, że prawdziwa jest hipoteza H₀.

Założenia:

1. testy dla średniej w populacji: X:N(m,σ)

przy czym dla dużej próby X:N(m,σ)

lub inny ale o skończonej wartości σ²

2. testy dla wariancji: X:N(m,σ)

3. testy dla wskaźnika struktury: n > 100

4. testy dla wskaźników współczynnika korelacji:

dwuwymiarowy rozkład normalny zmiennych X i Y

5. testy dla dwóch średnich: X₁:N(m₁,σ₁); X₂:N(m₂,σ₂)

przy czym test dla małej próby (max 3) dodatkowo σ²₁ = σ²₂

6. testy dla dwóch wariancji: X₁:N(m₁,σ₁); X₂:N(m₂,σ₂)

7. testy dla dwóch wskaźników struktury: n1, n2 > 100

Made by M@xell 2005

---